Mechanische Arbeit in einer Dimension

Verschiebt man ein Objekt entlang der Strecke $s$ mit der Konstanten Kraft $F$, so hat man die Arbeit

$$W = F\cdot s$$

geleistet. Ist die Kraft nicht konstant, so teilt man die Strecke in infinitesimal kleine Teilstrecken $ds$ auf und erhält für jede Teilstrecke die Arbeit

$$dW = F ds$$

Die einzelnen Teilarbeiten sind additiv, also erhält man als Definition der Arbeit

Die mechanische Arbeit ist

$$W(x_1\rightarrow x_2) = \int\limits_{x_1}^{x_2} F(x) dx = \int F(s) ds$$ (3.56)

Beschleunigungsarbeit oder kinetische Energie

Wir fragen uns nun: Was ist der Aufwand, um eine konstante Masse $m$ vom Impuls $p=0$ auf den Impuls $p$ zu bringen? Der Aufwand, die Beschleunigungsarbeit, hängt von zwei Grössen ab

• $\dot{p}$. Mit der Impulsänderung ändern wir auch die Geschwindigkeit oder die Masse oder beides.
• $ds$ Der Aufwand muss vom Weg abhängen.

Den Aufwand nennen wir die kinetische Energie. Wir schreiben unter Verwendung der Definition der Arbeit Gleichung (3.34) :

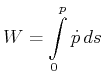$$W = \int\limits_0^p \dot{p} ds$$ (3.57)

Aus dem Experiment und der Definition des Impulses wissen wir, dass $p=mv$ oder $v = p/m$ ist. Nun ist aber auch

$$\frac{ds}{dt} = v$$

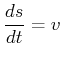und deshalb

$$ds = v dt =\frac{p}{m} dt$$

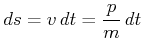Gleichzeitig wechseln die Integrationsgrenzen von $[0$,$\ell]$ zu $[0$,$t]$. Wir haben also

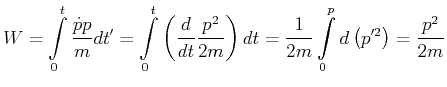$$W = \int\limits_0^t \frac{\dot{p}p}{m}dt'= \int\limits_0^t \left(... ...2m}\right) dt = \frac{1}{2m}\int\limits_0^p d\left(p'^2\right) = \frac{p^2}{2m}$$ (3.58)

das heisst, die Arbeit, um eine konstante Masse von 0 auf den Impuls $p$ zu bringen ist $W$. Diese Arbeit muss als kinetische Energie betrachtet werden. Sie steckt in der Bewegung der Masse $m$. Sollte die Masse veränderlich sein, kann immer die Masse temporär als konstant angesehen und die kinetische Energie mit dem obigen Verfahren berechnet werden.

kinetische Energie

$$E_{kin} = \frac{p^2}{2m}$$ (3.59)

Die Einheit der kinetischen Energie ist: $1Joule=1Nm$

Potentielle Energie

Unter potentieller Energie verstehen wir die Möglichkeit, Arbeit zu leisten, wobei wir die Energie, die in der Bewegung ist, ausklammern. Arbeit im physikalischen Sinne ist

$$dW = {F}_{ext}\cdot d{s}$$ (3.60)

Wir betrachten also nur die Komponente der Kraft $\vec{F}_{ext}$, die entlang des Wegelementes $d\vec{s}$ liegt.

Nun ist die Kraft, die das System aufbringt, die Kraft, gegen die wir arbeiten müssen, ${F}=-{F}_{ext}$. Die im System gespeicherte Energie ist deshalb

$$dW = {F}_{ext}\cdot d{s} = -{F}\cdot d{s}$$ (3.61)

Damit ist die potentielle Energie definiert durch

$$E_{pot}= -\int\limits_{s_1}^{s_2} {F}\cdot d{s}$$ (3.62)

Die Einheit der potentiellen Energie ist: $1Joule=1Nm$

Energieerhaltung mechanischer Systeme in einer Dimension

Versuch zur Vorlesung: Energieerhaltung (Versuchskarte M-093)

Wir betrachten ein System, dessen Energie konstant ist.

$$E_{tot} = E_{kin} + E_{pot} + E_{innen} = konstant$$ (3.63)

Dabei ist $E_{innen}$ die noch unspezifizierte innere Energie eines Teilchens. Für Massenpunkte ist $E_{innen}=0$.

Die Konstanz der gesamten Energie $E_{tot}$ bedeutet, dass deren zeitliche Ableitung null sein muss

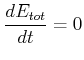$$\frac{d E_{tot}}{dt} = 0$$ (3.64)

Diese Gleichung ist ein Ausdruck des Hamiltonschen Prinzips, dass die Gesamtenergie konstant sei. Im Einzelnen hat man

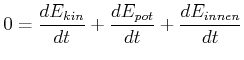$$0 = \frac{d E_{kin}}{dt}+\frac{dE_{pot}}{dt}+\frac{dE_{innen}}{dt}$$ (3.65)

Nehmen wir nun an, dass die innere Energie konstant sei (z.B. Massenpunkte). Dann ist

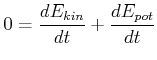$$0 = \frac{d E_{kin}}{dt}+\frac{dE_{pot}}{dt}$$ (3.66)

Eindimensionaler Spezialfall: $E_{pot}$ linear in $x$

Wir betrachten ein eindimensionales Problem und nehmen an, dass

$$E_{pot}=-F\cdot x$$

sei. Dann ist die Bewegungsgleichung

$$\frac{d}{dt}\left(E_{kin}+E_{pot}\right)=\frac{d}{dt}\left(\frac{1}{2m}{{p}}^2-Fx\right)=0$$

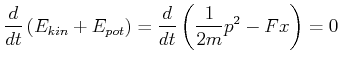
oder (mit $m=konst$)

$$\frac{1}{2m} 2{p}\cdot\dot{{p}}-F\dot x = 0$$

Umgeschrieben ist

$$p\cdot\dot{p} = mF\dot{x} = Fp$$

und mit $p\neq 0$

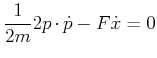
$$F = \dot{p}$$ (3.67)

Diese Bewegungsgleichung ist auch als 2. Newtonsches Axiom oder als 2. Newtonsches Kraftgesetz bekannt. Die Herleitung zeigt jedoch, dass dieses Gesetz, so nützlich es manchmal sein mag, kein fundamentales Gesetz, sondern ein aus den Symmetriebeziehungen des Raumes abgeleitetes Gesetz ist Emmy Noether, [Noe18].

Arbeit und Leistung

Versuch zur Vorlesung: Arbeit an der schiefen Ebene (Versuchskarte M-094)

Beispiel Hebel

$\Delta y=\Delta x$	$\Delta y=2\Delta x$
$F_{0}=mg$	$F_{0}=\frac{1}{2}mg$
$\Delta y\cdot F_{0}=\Delta x \cdot dm g$	$\Delta y\cdot F_{0}=mg\cdot\Delta x$

Kräftegleichgewicht beim Hebel

Die Grösse Weg$\times$   Kraft, also die Arbeit, wird beim Hebel erhalten.

$$dW ={F}_ \vert\vert s \cdot d{s}$$ (3.68)

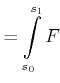$$W =\int\limits_{s_{0}}^{s_{1}}F_ \vert\vert s d{s}=W\left( s_{1}\right) -W\left( s_{0}\right)$$ (3.69)

Dabei ist $ds$ der Weg entlang der Bahn!

also

$${F}_ \vert\vert r \Rightarrow W =F\cdot s$$ (3.70)

$${F}_ \perp r \Rightarrow W =0!$$ (3.71)

Beispiel:

Kreisbahn ${a}_{zentripetal}\perp d{r}\Rightarrow W=0$

Die Einheit der Arbeit ist $1\frac{m^{2}kg}{s^{2}}=1 Joule =1J=1Nm=\frac {1}{3600000}kWh$

Im allgemeinen dreidimensionalen Falle hängt die Arbeit $W$ von der durchlaufenden Bahn $\vec{r}(s)$ ab.

Beispiel:

Luftwiderstand

$$F_{Luft} =bv^{2}$$

Wenn die Beschleunigung $a$ konstant ist, gilt

$$v\left( s\right) =\sqrt{2as}$$

Dann ist

$$W_{Luft}=\int\limits_{0}^{s_{0}}b v^{2}ds=\int\limits_{0}^{s_{0}}2a s\cdot b ds=ab\cdot s^{2}$$

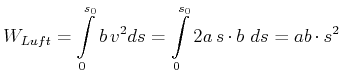Beispiel:

Bei der Gleitreibung haben wir

$$W\left( r_{1},r_{2},b\right) =\int\limits_{s_{2}}^{s_{1}}\left( -{F}_{G}\right) ds$$

$$=F_{G}\int\limits_{s_2}^{s_{1}}ds$$

$$=F_{G}\left( s_{2}-s_{1}\right)$$

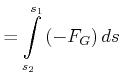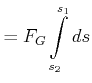Das heisst, die Arbeit ist, wie erwartet, proportional zur zurückgelegten Strecke.

Bei der Berechnung der Arbeit spielt Zeit keine Rolle. Wenn wir die Zeit, in der eine Arbeit geleistet wird, berücksichtigen wollen, sprechen wir von Leistung.

Definition der Leistung

$$P=\frac{dW}{dt}$$ (3.72)

Gleichung (3.50) kann mit der Definition der Arbeit umgeschrieben werden:

$$P = \frac{dW}{dt} = \frac{d}{dt}\int\limits_{r_0}^r F(s) ds$$

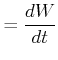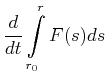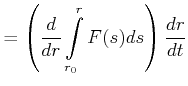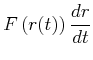$$= \left(\frac{d}{dr}\int\limits_{r_0}^r F(s) ds\right) \frac{dr}{dt} = F\left(r(t)\right)\frac{dr}{dt}$$ (3.73)

Wir haben bei der Umformung verwendet, dass die Ableitung nach der oberen Grenze (die untere ist hier konstant) eines Integral der Integrand selbst ist. Umgeschrieben erhalten wir

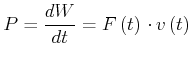$$P=\frac{dW}{dt}={F}\left( t\right) \cdot{v}\left( t\right)$$ (3.74)

Die Einheit der Leistung ist

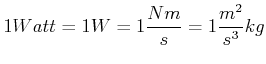$$1Watt=1W=1\frac{Nm}{s}=1\frac{m^{2}}{s^{3}}kg$$ (3.75)

Potentielle Energie und Kräfte

Aus der Definition der potentiellen Energie ersehen wir, dass

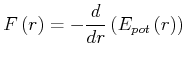$${F}\left( {r}\right) =-\frac{d}{dr}\left( E_{pot}\left( {r}\right) \right)$$ (3.76)

Der Beweis lautet:

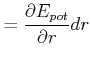$$d\left( E_{pot}\left( {r}\right) \right) =\frac{\partial E_{pot}}{\partial r}dr$$

$$=d\left[ -\int\limits_{{r}_{0}}^{{r}}{F}\left( {s}\right) d{s}\right] =-F\left( {r}\right) d{r}$$ (3.77)

Gleichgewicht und Stabilität

Versuch zur Vorlesung: Arten des Gleichgewichts (Versuchskarte M-021)

Um die Stabilität einer Gleichgewichtslage zu untersuchen, betrachten wir die drei möglichen Verläufe der potentiellen Energie mit einer Ortskoordinate

Gleichgewichtslagen und potentielle Energie

1. Bei einer Auslenkung ergibt sich eine Rückstellkraft: wir haben ein stabiles Gleichgewicht

   Bedingung ist: $\frac{\partial E}{dx}=0$, $\frac{d^{2}E}{dx^{2}}>0$ oder $\frac{dF}{dx}<0$

2. Bei einer Auslenkung ergibt sich eine zunehmende Kraft nach aussen: wir haben ein labiles Gleichgewicht

   Bedingung ist: $\frac{\partial E}{dx}=0$, $\frac{d^{2}E}{dx^{2}}<0$ oder $\frac{dF}{dx} >0$

3. Bei einer Auslenkung ist die Masse immer noch im Gleichgewicht: wir haben ein indifferentes Gleichgewicht

   Bedingung ist: $\frac{\partial E}{dx}=0$, $\frac{d^{2}E}{dx^{2}}=0$ oder $\frac{dF}{dx}=0$

In 3 Dimensionen ist ein Massenpunkt im Gleichgewicht, wenn ${}\boldsymbol{\mathrm{grad}}{} E_{pot}=0$ ist.