Weiter: Stösse Oben: Mechanik in drei Dimensionen Zurück: Dynamik Skript: PDF-Datei Übungen: Blätter ILIAS: Materialien Korrekturen
Wir betrachten ein System von Teilchen
![\includegraphics[width=0.6\textwidth]{mechanik-040}](img949.gif)
Skizze der Koordinaten in einem Teilchensystem
|
Die folgenden Grössen benötigen wir
Der Gesamtimpuls ist
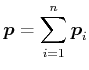 |
(4.227) |
Aus dem Impulssatz folgt
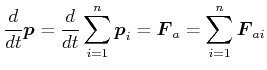 |
(4.228) |
Beweis
![]() Reaktionsprinzip
Reaktionsprinzip
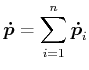 |
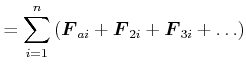 |
|
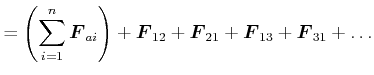 |
||
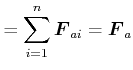 |
Wenn keine äusseren Kräfte wirken gilt:
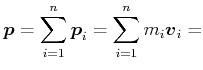 konstant konstant |
(4.229) |
Definition des Ortsvektors des Massenmittelpunktes
Der Ortsvektor des Massenmittelpunktes ist der mit der Masse gewichtete Mittelwert der Ortsvektoren der einzelnen Massepunkte. Aus Gleichung (4.133) bekommt man
Wir ersetzen die Summe durch das Integral und erhalten
Für eine kontinuierliche Massenverteilung gilt:
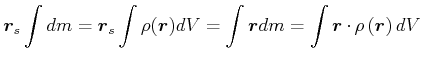 |
(4.232) |
oder
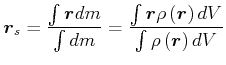 |
(4.233) |
In kartesischen Koordinaten gilt
![$\displaystyle \vec{r}_{s}=\left( \begin{array}[c]{c} x_{s} y_{s} z_{s} \end{array} \right)$](img967.gif) |
(4.234) |
mit
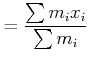 |
(4.235) | |
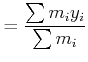 |
(4.236) | |
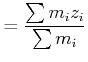 |
(4.237) |
|
|
|
|
Mit
![]() gilt:
gilt:
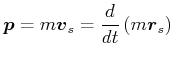 |
(4.238) |
Beweis
![\includegraphics[width=0.5\textwidth]{mechanik-041}](img976.gif)
|
Wir verwenden ein lokales Koordinatensystem. Weiter sei
![]() der Ortsvektor des
Punktes
der Ortsvektor des
Punktes ![]() im mitbewegten Koordinatensystem.
im mitbewegten Koordinatensystem.
wenn
![]()
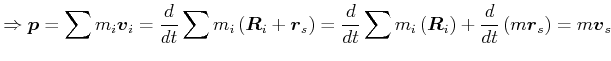
Aus
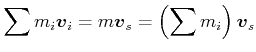 |
bekommt man für die Geschwindigkeit des Massenmittelpunktes
Die Massenmittelpunktsgeschwindigkeit ![]() ist also das mit den Massen gewichtete Mittel der einzelnen
Geschwindigkeiten.
ist also das mit den Massen gewichtete Mittel der einzelnen
Geschwindigkeiten.
Bei konstanten Massen
![]() gilt für die Beschleunigung des Massenmittelpunktes
gilt für die Beschleunigung des Massenmittelpunktes
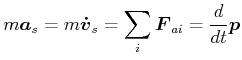 |
(4.240) |
Wenn keine äusseren Kräfte wirken folgt aus
| (4.241) |
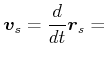 konstant konstant |
(4.242) |
Wir wollen nun die potentielle Energie einer Massenverteilung im Erdgravitationsfeld berechnen.
![\includegraphics[width=0.4\textwidth]{mechanik-042}](img989.gif)
|
Sei ![]() der Feldvektor des Gravitationsfeldes der Erde
der Feldvektor des Gravitationsfeldes der Erde
Für die Koordinate ![]() gilt
gilt
| (4.243) |
mit
![]() der Gesamtmasse. Die potentielle Energie ist dann
der Gesamtmasse. Die potentielle Energie ist dann
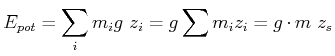 |
(4.244) |
![\includegraphics[width=0.4\textwidth]{mechanik-043}](img995.gif)
Definition der Grössen beim Zweikörperproblem.
|
Wir wollen die Bewegung der beiden Massen in einem mit dem Massenmittelpunkt mitbewegten Bezugssystem berechnen.
Seien die
![]() die Geschwindigkeiten im Massenmittelpunktssystem
die Geschwindigkeiten im Massenmittelpunktssystem
Im Laborsystem gilt nach Gleichung (4.142) :
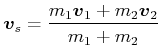 |
(4.245) |
Die Geschwindigkeiten im Massenmittelpunktssystem sind
Beispiel:
Kollision zweier Massen
![\includegraphics[width=0.7\textwidth]{mechanik-044}](img1004.gif)
Kollision zweier Massepunkte
|
Die Massenmittelpunktsgeschwindigkeit ist
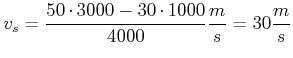 |
(4.247) |
Bei einer Kollision bleibt die Massenmittelpunktgeschwindigkeit
![]() bleibt erhalten. Die
Relativgeschwindigkeiten im Massenmittelpunktssystem sind
bleibt erhalten. Die
Relativgeschwindigkeiten im Massenmittelpunktssystem sind
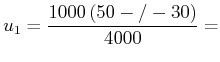 |
||
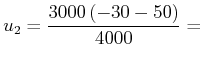 |
(4.248) |
Im Massenmittelpunktssystem hat die leichtere Masse die grössere Geschwindigkeit.
Die kinetische Energie eines Systems von Massen ist durch
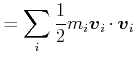 |
||
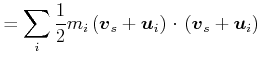 |
||
![$\displaystyle =\sum\limits_{i}\frac{1}{2}m_{i}\left[ \vec{v}_{s}^{2}+\vec{v}_{s}\vec{u}_{i}+\vec{u}_{i}\vec{v}_{s}+\vec{u}_{i}^{2}\right]$](img1014.gif) |
||
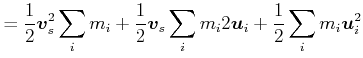 |
||
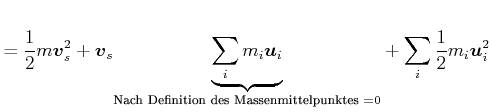 |
||
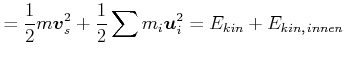 |
(4.249) |
Da die Massenmittelpunktsgeschwindigkeit erhalten bleibt, ist nur
![]() relevant für
Kollisionen
relevant für
Kollisionen
![]() Kollisionen mit gegenläufigen Bahnen beim Large Hadron Collider
(LHC).
Kollisionen mit gegenläufigen Bahnen beim Large Hadron Collider
(LHC).
Bei inelastischen Stössen kann nur die Energie
![]() in Wärme oder Deformation
umgewandelt werden.
in Wärme oder Deformation
umgewandelt werden.
Othmar Marti