Weiter: Statik des starren Körpers Oben: Mechanik starrer Körper Zurück: Mechanik starrer Körper Skript: PDF-Datei Übungen: Blätter ILIAS: Materialien Korrekturen
![\includegraphics[width=0.4\textwidth]{starr-001}](img2054.gif)
Definition: ein Körper ist starr, wenn
|
Die Massendichte (auch kurz Dichte genannt) ist definiert durch
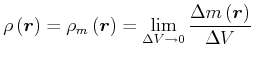 |
(6.526) |
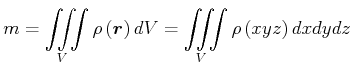 |
(6.527) |
Der Schwerpunkt ![]() eines starren Körpers hat bezüglich dieses Körpers eine fest Lage. Ein Körper kann in einem
homogenen Kraftfeld an seinem Schwerpunkt gestützt werden, und er is tim Gleichgewicht. Der Schwerpunkt ist
gegeben durch
eines starren Körpers hat bezüglich dieses Körpers eine fest Lage. Ein Körper kann in einem
homogenen Kraftfeld an seinem Schwerpunkt gestützt werden, und er is tim Gleichgewicht. Der Schwerpunkt ist
gegeben durch
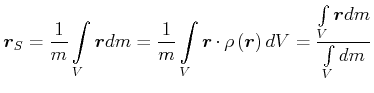 |
(6.528) |
![\includegraphics[width=0.4\textwidth]{starr-002}](img2062.gif)
Schwerpunktsystem
|
Im Laborsystem gilt
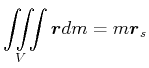 |
(6.529) |
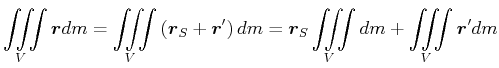 |
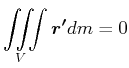 |
(6.530) |
![\includegraphics[width=0.4\textwidth]{starr-003}](img2067.gif)
|
Wir betrachten 2 Koordinatensysteme, beide mit dem Ursprung im Schwerpunkt S.
![]() ,
,![]() ,
,![]() ist das
raumfeste Koordinatensystem, d.h. es dreht sich nicht mit dem Körper mit.
ist das
raumfeste Koordinatensystem, d.h. es dreht sich nicht mit dem Körper mit.
![]() ,
,![]() ,
,![]() : ist ein
körperfestes Koordinatensystem, das sich mit dem Körper mitdreht. Die Koordinatensysteme werden durch die
Einheitsvektoren
: ist ein
körperfestes Koordinatensystem, das sich mit dem Körper mitdreht. Die Koordinatensysteme werden durch die
Einheitsvektoren
![]() ,
,![]() ,
,![]() und
und
![]() ,
,![]() ,
,![]() beschrieben.
beschrieben.
Also ist
| (6.531) |
![]() ,
,![]() ,
,![]() sind zeitunabhängige Basisvektoren,
sind zeitunabhängige Basisvektoren,
![]() ,
,![]() ,
,![]() sind zeitabhängige Basisvektoren.
sind zeitabhängige Basisvektoren.
Das Koordinatensystem
![]() ,
,![]() ,
,![]() geht durch drei Drehungen aus dem
Koordinatensystem
geht durch drei Drehungen aus dem
Koordinatensystem
![]() ,
,![]() ,
,![]() hervor.
hervor.
![\includegraphics[width=0.5\textwidth]{starr-004}](img2080.gif)
Definition der Eulerschen Winkel
|
Die Eulerschen Winkel sind
![]() steht senkrecht zur Ebene aufgespannt durch
steht senkrecht zur Ebene aufgespannt durch
![]() und
und
![]() .
.
Die Reihenfolge der Drehungen ist
|
|
Die Beziehungen zwischen dem ungesternten und dem gesternten Koordinatensystem können mit einer Matrix formuliert werden:
| (6.532) |
und
| (6.533) |
In Matrixschreibweise haben wir
![$\displaystyle \left( \begin{array}[c]{c} x^* y^* z^* \end{array} \right) ...
... \end{array} \right) \left( \begin{array}[c]{c} x y z \end{array} \right)$](img2098.gif) |
(6.534) |
und
![$\displaystyle \left( \begin{array}[c]{c} x y z \end{array} \right) =\left...
...array} \right) \left( \begin{array}[c]{c} x^* y^* z^* \end{array} \right)$](img2099.gif) |
(6.535) |
Wir haben hier behauptet, dass die Transformationsmatrix
![$\displaystyle T = \left( \begin{array}[c]{ccc} R_{11} & R_{12} & R_{13} R_{21} & R_{22} & R_{23} R_{31} & R_{32} & R_{33} \end{array} \right)$](img2100.gif) |
(6.536) |
und die inverse Transformationsmatrix
![$\displaystyle T^{-1} = \left(\begin{array}[c]{ccc} R_{11} & R_{21} & R_{31} R_{12} & R_{22} & R_{32} R_{13} & R_{23} & R_{33} \end{array} \right)$](img2101.gif) |
(6.537) |
durch
| (6.538) |
verbunden sind. Dabei ist ![]() die transponierte Matrix (an der Hauptdiagonale gespiegelt) und
die transponierte Matrix (an der Hauptdiagonale gespiegelt) und ![]() die
inverse Matrix.
die
inverse Matrix.
In Matrixschreibweise haben wir
Die Matrix ![]() berechnet sich aus dem Matrixprodukt der drei Drehmatrizen.
Dabei betrachten wir die Transformation aus dem ortsfesten System ins
mitbewegte System, also die Matrix
berechnet sich aus dem Matrixprodukt der drei Drehmatrizen.
Dabei betrachten wir die Transformation aus dem ortsfesten System ins
mitbewegte System, also die Matrix
![]() .
.
![\includegraphics[width=0.9\textwidth]{starr-028}](img2111.gif)
Wir betrachten die die
|
Dann ist
und
Die Drehungen um die ![]() folgt analog. Dann sind die Drehmatrizen gegeben durch
folgt analog. Dann sind die Drehmatrizen gegeben durch
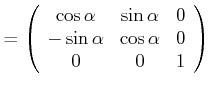 |
Drehung um |
(6.539) | |
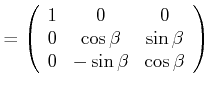 |
Drehung um |
(6.540) | |
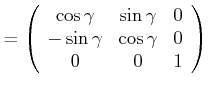 |
Drehung um |
(6.541) |
Dann ist
| (6.542) |
wobei die Multiplikation von rechts durchzuführen ist. Das Resultat ist
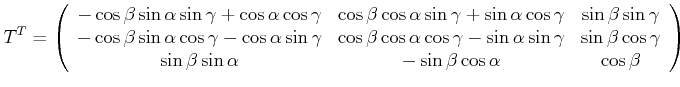 |
(6.543) |
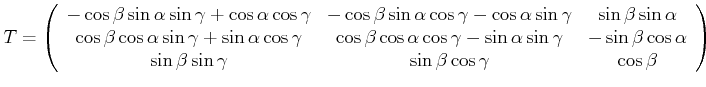 |
(6.544) |
oder
|
|
Beim einem allgemeinen rotierenden starren Körper sind die Eulerwinkel im Allgemeinen zeitabhängig!
Die Lage eines starren Körpers ist gegeben durch
Othmar Marti