__________________________________________________________________________
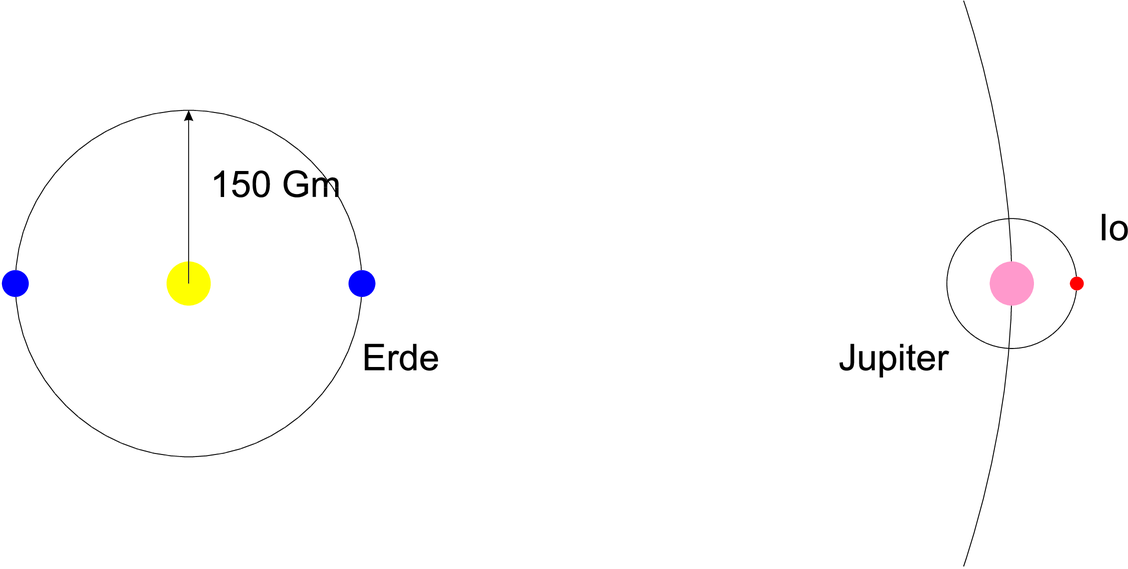
Bestimmung der Lichtgeschwindigkeit mit Hilfe der Periodendauer der Umlaufzeit des Jupitermondes Io.
_____________________________________________________________________

| Literatur | |
__________________________________________________________________________

Bestimmung der Lichtgeschwindigkeit mit Hilfe der Periodendauer der Umlaufzeit des Jupitermondes Io.
_____________________________________________________________________
Astronomische Beobachtungen waren schon immer sehr genau. Ole Rømer beobachtete 1675 dass der Eintritt des Jupitermondes Io in den Kernschatten sich abhängig von den Sternkonstellationen verschob. Die Periode der Umlaufzeit beträgt 42.5 Stunden und nimmt zu, wenn die Erde sich vom Jupiter weg bewegt und ab, wenn sie sich auf den Jupiter zu bewegt. Der maximale Zeitunterschied ist 2·150·109 m∕3·108 m/s = 1000 s. Zwischen zwei Eintritten in den Kernschatten ist der Zeitunterschied zum mittleren Zeitunterschied 150·109 m∕(365.24 ∗ 24 h).5 h∕3·108 m/s = 2.42 s. Ole Rømer brauchte also eine Uhr, die in 24 h weniger als eine Sekunde Fehler hatte. Ole Rømer mass eine Lichtgeschwindigkeit von ungefähr 2·108 m/s. Daraus kann geschlossen werden, dass seine Zeitmessung eine relative Genauigkeit von 3·10−7 hatte, besser als manche Armbanduhr heute.
Eine gewaltige Verbesserung der Genauigkeit erzielte Bradley mit seiner Beobachtung der Aberration des Lichtes. Analog zum Regen, der, wenn man steht von oben kommt und der wenn man geht schräg von vorne fällt, ändert das Licht seine Einfallsrichtung. Aus der Winkeländerung kann auf die Lichtgeschwindigkeit geschlossen werden, wenn man die Eigengeschwindigkeit kennt.
__________________________________________________________________________
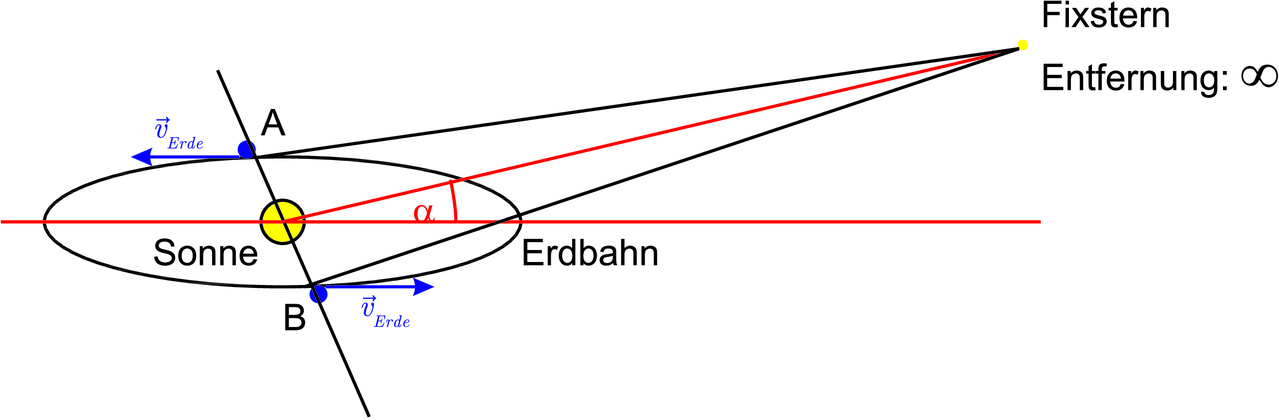
Bradley beobachtete die Position eines Fixsterns (möglichst unendlich weit weg) zu verschiedenen Zeiten.
_____________________________________________________________________
In der Abbildung sind zwei extreme Positionen aufgezeichnet, da wo die Erde mit maximaler Geschwindigkeit auf den Stern sich hinbewegt und da, wo sie sich mit maximale Geschwindigkeit entfernt. Die Bahngeschwindigkeit der Erde ist etwa vErde = 3·104 m/s. Alternativ könnte man die Position des Sterns auch im Abstand von 12 Stunden ausmessen. dabei müsste die Umfangsgeschwindigkeit, die in Ulm etwa vUmfang,Ulm = 327 m/s und damit etwa 100 mal kleiner ist, verwendet werden.
__________________________________________________________________________
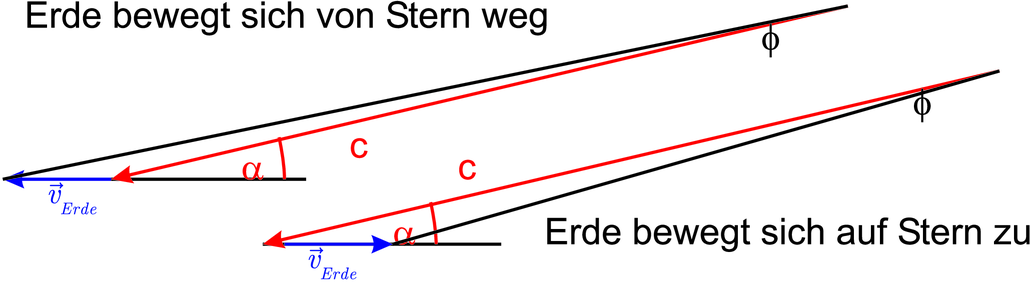
Dreiecke zur Berechnung der Lichtgeschwindigkeit nach Bradley
_____________________________________________________________________
Zur Berechnung verwenden wir den Sinussatz:
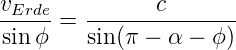 | (5.1) |
Praktischerweise ergeben sich für beide Fälle, sowohl auf die Erde zu wie von der Erde weg die gleiche Gleichung. Diese Beziehung formen wir um
Für kleine Winkel ϕ «π bekommen wir
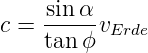 | (5.3) |
Wie gross ist nun der zu messende Winkel ϕ? Wir betrachten einen Stern,d er etwa π∕4 über der Ekliptik (der Bahnebene der Erde) liegt. Mit vErde = 30 km/s und c = 300000 km/s und α = π∕4 erhalten wir
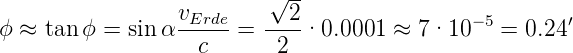 | (5.4) |
Der gemessene Winkelunterschied zwischen den Punkten A und B ist somit
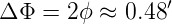 | (5.5) |
Wenn wir nur im Zeitabstand von einem Tag messen, ist der der Winkel ΔΦ = 0, 29′′.
__________________________________________________________________________
_____________________________________________________________________
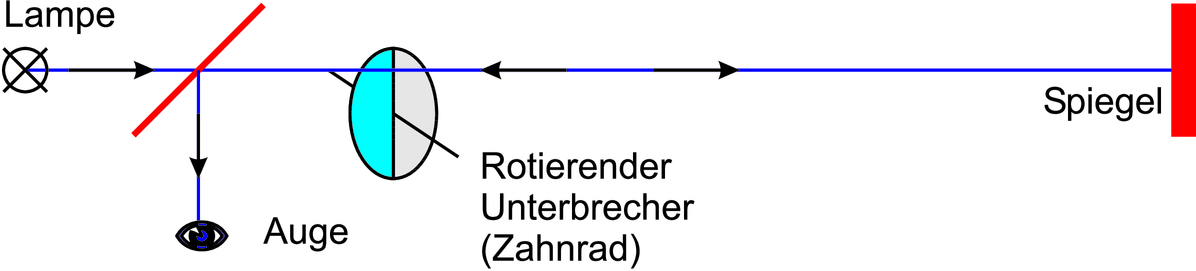
Fizeau verwendete einen Weg von 8.63 km. Bei bestimmten Geschwindigkeiten (welchen?) wurde der Weg des Lichtes blockiert, bei anderen durchgelassen. Nehmen wir an, dass das Zahnrad mit 100 Umdrehungen pro Sekunde rotiere. Das Licht wird blockiert, wenn das Zahnrad sich um einen halben Zahn weiter dreht in der Laufzeit des Lichts. Die Laufzeit ist t = 8630 m∕3·108 m/s = 2.877·10−5 s. Die Umdrehungszeit des Rades ist 0.01 s. Also hat das Rad n = 0.01∕(2 × 2.877·10−5) = 174 Zähne, machbar!.
__________________________________________________________________________
_____________________________________________________________________
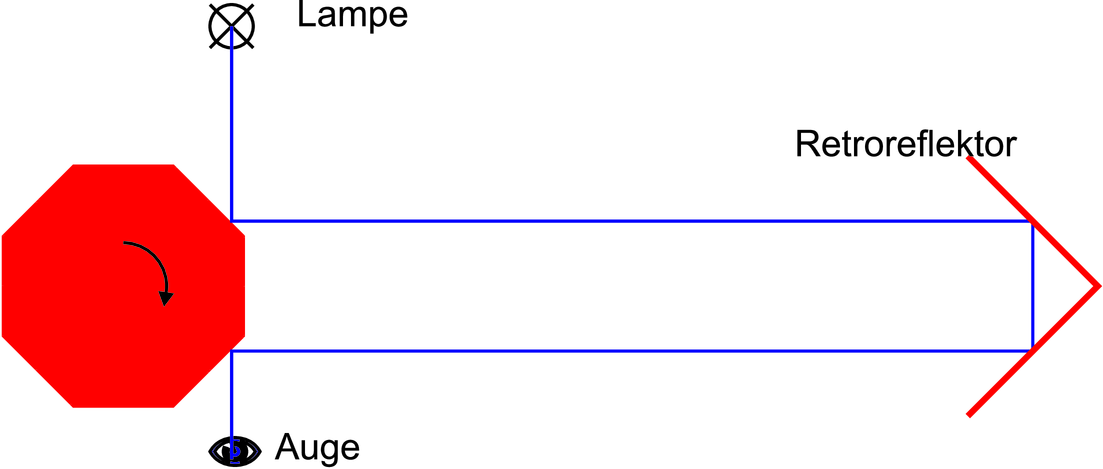
| Versuch zur Vorlesung: | |
| Messung der Lichtgeschwindigkeit mit der Drehspiegelmethode (Versuchskarte O-030) | |
Eine verbesserte Methode ist die Messung der Lichtgeschwindigkeit nach Leon Foucault. Er verwendete einen Drehspiegel. Seine Genauigkeit war so gross, dass er auch den Unterschied der Lichtgeschwindigkeit in stehendem und fliessendem Wasser messen konnte.
Heute wird die Lichtgeschwindigkeit mit moderner Elektronik gemessen.
Die Lichtgeschwindigkeit im Vakuum beträgt
299792458 . Sie ist eine Definitionsgrösse. . Sie ist eine Definitionsgrösse. |
 Lizenzinformationen
Lizenzinformationen