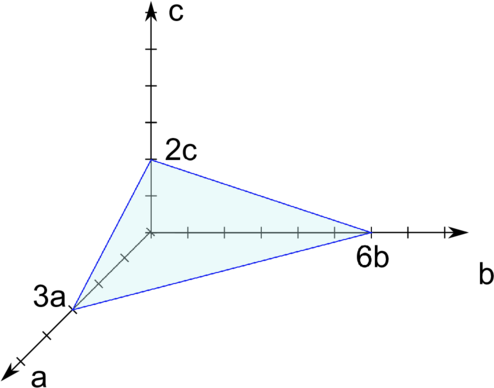
| Abbildung J.1.: | Skizze zur Bestimmung der Miller’schen Indizes |

Oberflächen werden durch Millersche Indizes (hkl) beschrieben. Abbildung J.1 zeigt ein Beispiel einer Volumennetzebene. Die Millerschen Indizes werden wie folgt bestimmt:
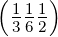
Die in Abbildung J.1 eingezeichnete Ebene ist die (2, 1, 3)-Ebene. Negative Indizes werden mit = −2 angegeben.
Periodische Strukturen auf einer Fläche werden durch Bravais-Netze beschreiben. (Diese sind analog zu den Bravais-Gittern in drei Dimensionen). Der Ort einer Zelle im Netz einer periodischen Oberfläche ist durch
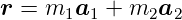 | (J.1) |
gegeben. Die Vektoren 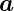 1 und
1 und 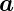 2 heissen Basisvektoren.
Die Zuordnung zu den Indizes "1" und "2" wird durch zwei
Konventionen bestimmt. Erstens muss
2 heissen Basisvektoren.
Die Zuordnung zu den Indizes "1" und "2" wird durch zwei
Konventionen bestimmt. Erstens muss 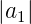 <
< 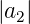 sein und
zweitens muss γ = ∠
sein und
zweitens muss γ = ∠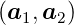 ≥ 90∘ sein. Weiter sollte γ − 90∘
minimal sein.
≥ 90∘ sein. Weiter sollte γ − 90∘
minimal sein.
Die folgenden Bravais-Netze werden an Oberflächen unterschieden:
| 1) quadratisch | 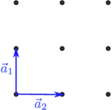 |
|
|||
| 2) rechteckig | 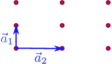 |
|
|||
| 3) schiefwinklig |  |
|
|||
| 4) hexagonal | 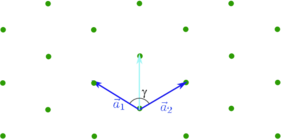 |
|
|||||
| 5) rechtwinklig,
zentriert (nicht
primitiv) | 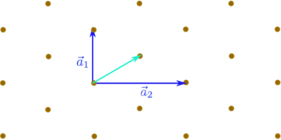 |
|
|||||
Beim schiefwinkligen Gitter (Nummer 3) ist grün eine zweite mögliche Wahl der Einheitsvektoren eingezeichnet. Dabei ist jedoch der Winkel γ kleiner als 90∘. Deshalb ist diese Wahl der Einheitsvektoren falsch.
Bei den Volumengittern werden aus den Bravais-Gittern die Raumgruppen, indem man die Motive der Einheitszellen betrachtet. Diese können zum Beispiel eine andere Symmetrie als das zugrunde liegende Gitter haben.Bei den Oberflächennetzen führt die Berücksichtigung der Motive in den Einheitszellen zu 17 Flächengruppen.
Anders als bei Netzen in einer Ebene müssen bei Oberflächennetzen alle unter einer Oberflächenzelle liegenden Atome als Basis berücksichtigt werden. Die Basisatome liegen also nicht in einer Ebene. Abbildung J.2 zeigt ein Beispiel.
Als Grundlage zur Beschreibung von Oberflächen dient die hypothetische Oberfläche, die beim Entzweischneiden eines Kristalls entsteht. Die Oberflächenstruktur wird bezogen auf diese hypothetische Oberfläche spezifiziert.
Abbildung J.3 zeigt als Beispiel wie eine Überstruktur
entsteht. Wenn man in der quadratischen Anordnung auf der
linken Seite jeweils jede 2. Reihe nach links rückt, erhältm
man die auf der rechten Seite gezeigte Überstruktur. Wenn wir
die das Netz der Überstruktur aufspannenden Basisvektoren
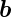 1 und
1 und 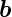 2 nennen, dann können wir schreiben
2 nennen, dann können wir schreiben
Die Überstruktur in der Abbildung J.3 rechts ist demnach eine (1 × 2)- Überstruktur oder auch eine (1 × 2)-Rekonstruktion.
Im allgemeinen sind die Vektoren 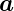 1 und
1 und 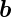 1 sowie
1 sowie 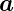 2 und
2 und
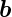 2 nicht parallel. Der Winkel ∠
2 nicht parallel. Der Winkel ∠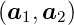 kann vom Winkel
∠
kann vom Winkel
∠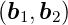 verschieden sein.
verschieden sein.
Gilt ∠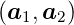 = ∠
= ∠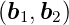 so gilt für die Beschreibung der
Überstruktur folgendes Rezept:
so gilt für die Beschreibung der
Überstruktur folgendes Rezept:
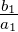 und
und 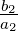 und bestimmt den Winkel γ
zwischen den Netzen ai und bi.
und bestimmt den Winkel γ
zwischen den Netzen ai und bi.
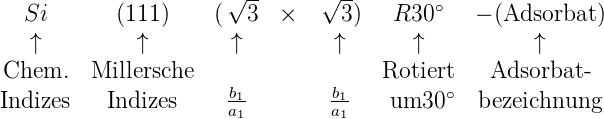
an. p nach den Millerschen Indizes gibt eine primitive Struktur an, c eine zentrierte Struktur.
Abbildung J.4 zeigt als Beispiel eine
Si(111)(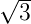 ×
×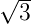 )R30∘-Rekonstruktion. Wird die Überstruktur
durch Fremdatome erzeugt, so werden deren chemische
Bezeichnungen hinten angefügt.
)R30∘-Rekonstruktion. Wird die Überstruktur
durch Fremdatome erzeugt, so werden deren chemische
Bezeichnungen hinten angefügt.
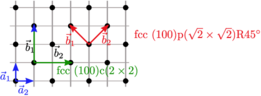
| Abbildung J.5.: | Beispiel einer Rekonstruktion, deren Bezeichnung nicht eindeutig festgelegt werden kann. |
Es gibt Rekonstruktionen, die, wenn man auch nichtprimitive
Einheitszellen zulässt, auf mehrere Arten bezeichnet
werden können. Die Abbildung J.5 zeigt ein Beispiel.
Die Rekonstruktion kann wie in der Abbildung links
gezeigt, als eine fcc(100)c(2 × 2)-Rekonstruktion oder als
fcc(100)p(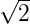 ×
×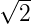 )R45∘-rekonstruktion bezeichnet
werden.
)R45∘-rekonstruktion bezeichnet
werden.
Es gibt Rekonstruktionen, die mit dem obigen Schema nicht zu beschreiben sind. In jedem Falle ist die Matrixschreibweise anwendbar.
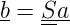 | (J.4) |
oder ausgeschrieben
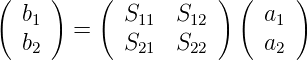 | (J.5) |
Die Matrixschreibweise funktioniert auch bei transzendenten Koeffizienten. Die beiden Beispiele illustrieren die Matrixschreibweise.
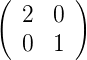
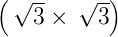 R30∘ ⇒S =
R30∘ ⇒S = 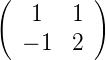
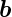 1 + m2
1 + m2 2 gleichartige Gitterplätze bezüglich der
Unterlage)
2 gleichartige Gitterplätze bezüglich der
Unterlage)
 Lizenzinformationen
Lizenzinformationen