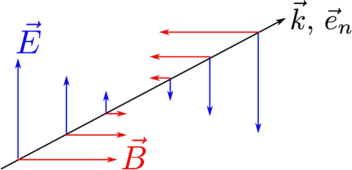
| Abbildung A.1.: | Schematische Darstellung einer elektromagnetischen Welle. |

In einem Medium mit der relativen Dielektrizitätskonstanten 𝜀 und der relativen Permeabilität μ ist eine der möglichen Lösungen der Maxwellgleichungen (A.2) die Wellenlösungen[Wei95]. Wir setzen an:
und erhalten mit der ersten Maxwellgleichung 
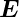 = −
= −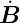 .
Somit ist
.
Somit ist
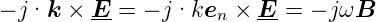 | (A.3) |
Als Folge der anderen Maxwellgleichungen haben wir für
den Wellenvektor k = ω∕c und für die Phasengeschwindigkeit
im Medium c = c0∕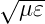 sowie für die Phasengeschwindigkeit
im Vakuum c0 = 1∕
sowie für die Phasengeschwindigkeit
im Vakuum c0 = 1∕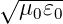 . Also wird Gleichung (A.3)
. Also wird Gleichung (A.3)
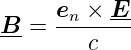 | (A.4) |
Daraus können wir den Wellenwiderstand im Medium als das Verhältnis der Amplituden des elektrischen und des magnetischen Feldes bestimmen.
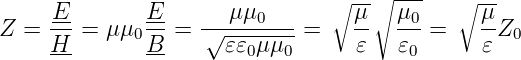 | (A.5) |
Dabei ist
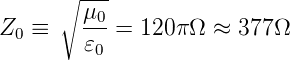 | (A.6) |
Der Wellenwiderstand charakterisiert offensichtlich die Ausbreitungseigenschaften von Transversalen ElektroMagnetischen Wellen oder TEM-Wellen.
 Lizenzinformationen
Lizenzinformationen