$\includegraphics[width=0.3\textwidth]{Bilder/bewegung-vektorkomponenten.eps}$

$\displaystyle A = (A_1,A_2) = \left(\begin{array}{c}A_1 A_2\end{array}\right)$ (3.36)

Länge

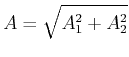$\displaystyle A = \sqrt{A_1^2 + A_2^2}$

(3.37)

Winkel mit der x-Achse

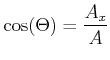$\displaystyle \cos(\Theta) = \frac{A_x}{A}$

(3.38)

Einheitsvektoren in x-Richtung, in y-Richtung, -in z-Richtung.

$\displaystyle \mathbf{A} = \vec{A}= A_x \vec{e}_x + A_y \vec{e}_y + A_z \vec{e}_z$

(3.39)

Addition

$\includegraphics[width=0.4\textwidth]{Bilder/bewegung-vektorkomponenten-addition.eps}$

$\displaystyle \vec{A}+ \vec{B}$	$\displaystyle =$	$\displaystyle (A_x \vec{e}_x + A_y \vec{e}_y + A_z \vec{e}_z) + (B_x \vec{e}_x + B_y \vec{e}_y + B_z \vec{e}_z)$
	$\displaystyle =$	$\displaystyle (A_x +B_x) \vec{e}_x + (A_y +B_y) \vec{e}_y + (A_z + B_z)\vec{e}_z$	(3.40)

Geschwindigkeitsvektor

$\displaystyle \vec{r}= x \vec{e}_x + y \vec{e}_y + z \vec{e}_z$

(3.41)

Mittlere Geschwindigkeit

$\includegraphics[width=0.5\textwidth]{Bilder/bewegung-vektor-ableitung.eps}$

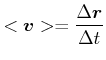$\displaystyle <\vec{v}> = \frac{\Delta \vec{r}}{\Delta t}$

(3.42)

Momentangeschwindigkeit

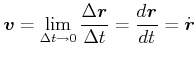$\displaystyle \vec{v}= \lim_{\Delta t \rightarrow 0} \frac{\Delta \vec{r}}{\Delta t} = \frac{d \vec{r}}{dt} =\dot {\vec{r}}$

(3.43)

Ableitung in Komponenten

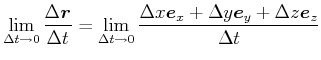$\displaystyle \vec{v}$	$\displaystyle =$	$\displaystyle \lim_{\Delta t \rightarrow 0} \frac{\Delta \vec{r}}{\Delta t} = \... ... 0} \frac{\Delta x \vec{e}_x + \Delta y \vec{e}_y+\Delta z \vec{e}_z}{\Delta t}$
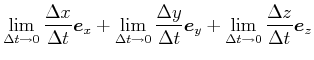	$\displaystyle =$	$\displaystyle \lim_{\Delta t \rightarrow 0} \frac{\Delta x}{\Delta t}\vec{e}_x ... ... t}\vec{e}_y + \lim_{\Delta t \rightarrow 0} \frac{\Delta z}{\Delta t}\vec{e}_z$	(3.44)

also

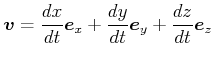$\displaystyle \vec{v}= \frac{dx}{dt}\vec{e}_x + \frac{dy}{dt}\vec{e}_y + \frac{dz}{dt}\vec{e}_z$

(3.45)

Analog zur obigen Rechnung erhält man die Beschleunigung aus der Geschwindigkeit.

Mittlere Beschleunigung

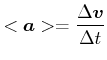$\displaystyle <\vec{a}> = \frac{\Delta \vec{v}}{\Delta t}$

(3.46)

Momentanbeschleunigung

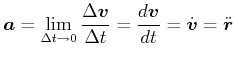$\displaystyle \vec{a}= \lim_{\Delta t \rightarrow 0} \frac{\Delta \vec{v}}{\Delta t} = \frac{d \vec{v}}{dt} =\dot {\vec{v}} = \ddot {\vec{r}}$

(3.47)

oder auch

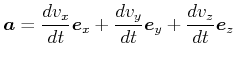$\displaystyle \vec{a}= \frac{dv_x}{dt}\vec{e}_x+\frac{dv_y}{dt}\vec{e}_y+\frac{dv_z}{dt}\vec{e}_z$

(3.48)

Relativgeschwindigkeit

$\includegraphics[width=0.5\textwidth]{bilder/bewegung-relativgeschw.eps}$

$\displaystyle \vec{v}_{Mensch\;gegen\;Erde} = \vec{v}_{Bus \;gegen \;Erde}+\vec{v}_{Mensch\; gegen\; Bus}$

(3.49)

Materialien

Bsp: Wurfbewegung

Dieser Stoff wurde am 23.10.2001 behandelt

(Siehe Tipler, Physik[Tip94, 53])

Wurfbewegungen sind zusammengesetzte Bewegungen (Beispiel aus (Siehe Tipler, Physik[Tip94, 53]) )

Siehe auch Simulation von Walter Fendt Uni Heidelberg oder Uni Würzburg.

$\includegraphics[width=0.3\textwidth]{Bilder/bewegung-wurf-anf.eps}$

$\includegraphics[width=0.4\textwidth]{Bilder/bewegung-wurf-zeit.eps}$
Bild aus (Siehe Tipler, Physik[Tip94, 55]) . Rot ist die horizontale, grün die vertikale Position markiert. Die horizontalen Abstände sind, innerhalb meiner Zeichengenauigkeit, gleich, deuten also auf eine konstante Geschwindigkeit hin.

Beschleunigungen

Sei , , $v_x(t=0) = v_{x,0}$ und $v_y(t=0) = v_{y,0}$

$\displaystyle a_y(t)$	$\displaystyle =$	$\displaystyle -g$
$\displaystyle a_x(t)$	$\displaystyle =$	0	(3.50)

Geschwindigkeiten

$\displaystyle v_y(t)$	$\displaystyle =$	$\displaystyle -g *t +v_{y,0}$
$\displaystyle v_x(t)$	$\displaystyle =$	$\displaystyle v_{x,0}$	(3.51)

Ort

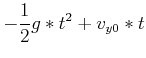$\displaystyle y(t)$	$\displaystyle =$	$\displaystyle - \frac{1}{2}gt^2 +v_{y,0}t$
$\displaystyle x(t)$	$\displaystyle =$	$\displaystyle v_{x,0}*t$	(3.52)

Diese Bewegung ist parabelförmig, wie man leicht sieht, wenn man nach auflöst und einsetzt.

$\displaystyle y(x) = - \frac{1}{2} d \left(\frac{x}{v_{x,0}}\right)^2 + \frac{v_{y,0}}{v_{x,0}} x$

(3.53)

Gleichförmige Kreisbewegung (mit vektorieller Darstellung)

Dieser Stoff wurde am 23.10.2001 behandelt

(Siehe Tipler, Physik[Tip94, 61]) (Siehe Gerthsen, Physik[GV95, 16])

Siehe auch Uni Würzburg oder von Walter Fendt.

Kreisförmige Bewegungen gibt es

Fahrt durch eine Kurve mit Fahrrad, Auto, Schlittschuhen ...
Zentrifuge
Satelliten

$\includegraphics[width=0.5\textwidth]{Bilder/bewegung_kreis_1.eps}$

Schematische Darstellung eines Satelliten

Der Satellit $\vert\vec{ }v\vert = v$ bewegt sich im Kreis mit dem Radius . In kleinen Zeiten bewegt er sich um in der ursprünglichen Richtung weiter. Er fällt um . Der Satz des Pythagoras angewandt auf das rechtwinklige Dreieck ergibt

$\displaystyle r^2 + (vt)^2 = (r+h)^2 = r^2 + 2 rh +h^2$

(3.54)

Kleine Zeiten bedeutet, dass $h \ll r$ ist. Also kann

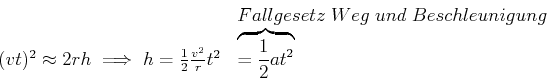$\begin{displaymath}\begin{array}{cl} &Fallgesetz,\;Weg\;und\;Beschleunigung\ (... ...\frac{v^2}{r} t^2 &\overbrace{= \frac{1}{2} a t^2} \end {array}\end{displaymath}$

(3.55)

geschrieben werden.

Vergleich

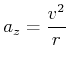$\displaystyle a_z = \frac{v^2}{r}$

(3.56)

Wenn $\vec{r}(t) = (r \cos(\omega t),r \sin (\omega t), 0)$ ist ( $\omega$ heisst Kreisfrequenz und wird benötigt, um aus der Zeit eine als Argument der Winkelfunktion benötigte dimensionslose Grösse zu erzeugen), dann ist

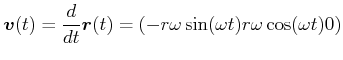$\displaystyle \vec{v}(t) = \frac{d}{dt}\vec{r}(t) = (- r \omega \sin(\omega t), r \omega \cos(\omega t),0)$

(3.57)

und

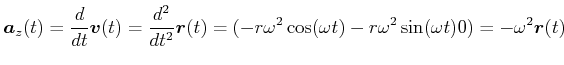$\displaystyle \vec{a}_z(t) = \frac{d}{dt}\vec{v}(t) = \frac{d^2}{dt^2}\vec{r}(t... ... \omega^2 \cos(\omega t), - r \omega^2 \sin(\omega t),0) = -\omega^2 \vec{r}(t)$

(3.58)

$\includegraphics[width=0.5\textwidth]{Bilder/bewegung-kreis-zentripetal.eps}$

Zentripetalbewegung. Die durch $\vec{r}_1,\vec{r}_2$ und durch $\vec{v}_1,\vec{v}_2$ aufgespannten Dreiecke sind ähnlich

Materialien

Masse auf Kreisbahn mit Gegengewicht

Nichtkommutativität endlicher Drehungen

Materialien

Folien zur Vorlesung am 24. 10. 2001 PDF

Dieser Stoff wurde am 24.10.2001 behandelt

$\includegraphics[width=0.4\textwidth]{Bilder/bewegung-drehung-endl-1.eps}$ $\includegraphics[width=0.4\textwidth]{Bilder/bewegung-drehung-endl-2.eps}$

Beispiel für die Nichtvertauschbarkeit endlicher Drehungen

Die mathematische Darstellung eine Drehung um die z-Achse kann wie folgt hergeleitet werden:

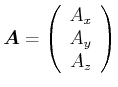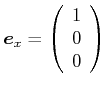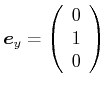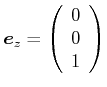Jeder Vektor $\vec{A}= \left(\begin{array}{c}A_x\\ A_y\\ A_z\\ \end{array}\right)$ kann als $\vec{A}= A_x \vec{e}_x + A_y \vec{e}_y + A_z \vec{e}_z$ geschrieben werden. Dabei ist $\vec{e}_x = \left(\begin{array}{c}1\\ 0\\ 0\\ \end{array}\right)$ , $\vec{e}_y = \left(\begin{array}{c}0\\ 1\\ 0\\ \end{array}\right)$ , und $\vec{e}_z = \left(\begin{array}{c}0\\ 0\\ 1\\ \end{array}\right)$ .

Die Funktion $R_z(\vec{A}, \alpha)$ soll den Vektor $\vec{A}$ um die z-Achse drehen.

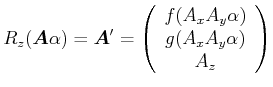Wenn der Vektor $\vec{A}$ um die z-Achse gedreht wird, dann ist der gedrehte Vektor $R_z(\vec{A}, \alpha) = \vec{A}' = \left(\begin{array}{c}f(A_x,A_y, \alpha)\\ g(A_x,A_y, \alpha)\\ A_z\\ \end{array}\right)$ . Die z-Komponente wird dabei nicht verändert, die x- und die y-Komponenten sind Funktionen der ursprünglichen x- und y-Komponenten sowie des Winkels.

$\includegraphics[width=0.6\textwidth]{Bilder/bewegung-vektor-z.eps}$

In der Abbildung links wird gezeigt, wie $\vec{e}_x$ transformiert wird. Rechts wird $\vec{e}_y$ transformiert.

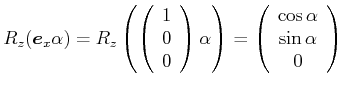Wir erhalten: $R_z(\vec{e}_x,\alpha) = R_z\left(\left(\begin{array}{c}1\\ 0\\ 0\\ \end{ar... ...ht) = \left(\begin{array}{c}\cos\alpha\\ \sin\alpha\\ 0\\ \end{array}\right)$ .

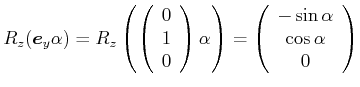$R_z(\vec{e}_y,\alpha) = R_z\left(\left(\begin{array}{c}0\\ 1\\ 0\\ \end{arr... ...t) = \left(\begin{array}{c}-\sin\alpha\\ \cos\alpha\\ 0\\ \end{array}\right)$ .

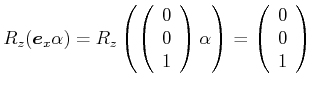$R_z(\vec{e}_x,\alpha) = R_z\left(\left(\begin{array}{c}0\\ 0\\ 1\\ \end{array}\right),\alpha\right) = \left(\begin{array}{c}0\\ 0\\ 1\\ \end{array}\right)$ .

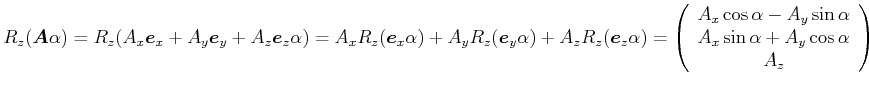Mit $R_z (\vec{A},\alpha) =R_z(A_x\vec{e}_x + A_y\vec{e}_y +A_z\vec{e}_z,\alpha)= A... ... A_y \sin\alpha\\ A_x \sin\alpha + A_y\cos\alpha\\ A_z\\ \end{array}\right)$ .

Diese letztere Gleichung kann als

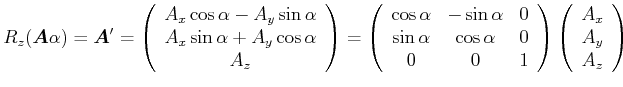$\displaystyle R_z(\vec{A},\alpha) = \vec{A}' = \left(\begin{array}{c}A_x \cos\a... ...\end{array}\right)\left(\begin{array}{c}A_x\\ A_y\\ A_z\\ \end{array}\right)$

(3.59)

Damit kann eine Drehung um die Z-Achse kann als Matrix

$\displaystyle D_z(\alpha) = \left(\begin{array}{ccc} \cos(\alpha)&-\sin(\alpha)&0 \sin(\alpha)& \cos(\alpha)&0 0&0&1 \end{array}\right)$

(3.60)

Durch formales ''Rotieren'' der Koordinaten $z \rightarrow y$ , $y \rightarrow x$ und $x \rightarrow z$ bekommt man die Drehmatrix für eine Drehung um die y-Achse

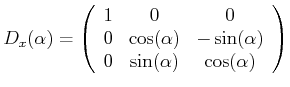$\displaystyle D_y(\alpha) = \left(\begin{array}{ccc} \cos(\alpha)&0&\sin(\alpha) 0&1&0 -\sin(\alpha)& 0&\cos(\alpha) \end{array}\right)$

(3.61)

Weiteres formales ''Rotieren'' der Koordinaten $z \rightarrow y$ , $y \rightarrow x$ und $x \rightarrow z$ liefert die Drehmatrix für eine Drehung um die x-Achse

$\displaystyle D_x(\alpha) = \left(\begin{array}{ccc} 1&0&0 0& \cos(\alpha)&-\sin(\alpha) 0&\sin(\alpha)& \cos(\alpha) \end{array}\right)$

(3.62)

Die Drehung um die y-Achse um $-\pi/2$ (=90°) und dann um die x-Achse um $-\pi/2$ wird mit Matrizen als

$\displaystyle \vec{r}'$	$\displaystyle =$	$\displaystyle D_x(-\pi/2) D_y(-\pi/2) \vec{r}$
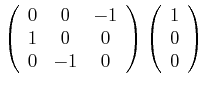	$\displaystyle =$	$\displaystyle \left(\begin{array}{ccc} 1&0&0\\ 0&0&1\\ 0&-1& 0\\ \end{array}... ...&0\\ \end{array}\right) \left(\begin{array}{c} 1 0 0\\ \end{array}\right)$
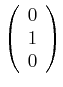	$\displaystyle =$	$\displaystyle \left(\begin{array}{ccc} 0&0&-1\\ 1&0&0\\ 0&-1&0\\ \end{array}\right) \left(\begin{array}{c} 1 0 0\\ \end{array}\right)$
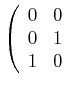	$\displaystyle =$	$\displaystyle \left(\begin{array}{c} 0 1 0\\ \end{array}\right)$	(3.63)

Werden die Drehungen in umgekehrter Reihenfolge durchgeführt, so ist

$\displaystyle \vec{r}'$	$\displaystyle =$	$\displaystyle D_x(-\pi/2) D_y(-\pi/2) \vec{r}$
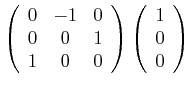	$\displaystyle =$	$\displaystyle \left(\begin{array}{ccc} 0&0&-1\\ 0&1&0\\ 1& 0&0\\ \end{array}... ... 0\\ \end{array}\right) \left(\begin{array}{c} 1 0 0\\ \end{array}\right)$
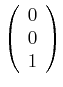	$\displaystyle =$	$\displaystyle \left(\begin{array}{ccc} 0&-1&0\\ 0&0&1\\ 1&0&0\\ \end{array}\right) \left(\begin{array}{c} 1 0 0\\ \end{array}\right)$
	$\displaystyle =$	$\displaystyle \left(\begin{array}{c} 0 0 1\\ \end{array}\right)$	(3.64)

Grosse Drehungen können nicht vertauscht werden. Es gibt viele Eigenschaften in der Physik, die nicht kommutativ sind

Next: Dynamik, die Newtonschen Axiome Up: Kinematik Previous: Bewegung in einer Dimension Skript: PDF-Datei Übungen: Blätter

Othmar Marti
Experimentelle Physik
Universiät Ulm