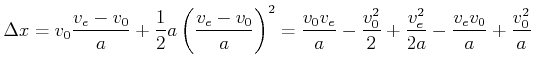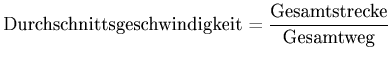 |
(3.12) |
| Dieser Stoff wurde am 16.10.2001 behandelt |
Aus dem Alltagsleben:
Physik: Mathematische Formulierung
Gesamtweg:
| (3.13) |
Gesamtzeit:
| (3.14) |
Wir schreiben für die Durchschnittsgeschwindigkeit
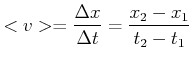 |
(3.15) |
Was ist die Durchschnittsgeschwindigkeit bei drei Strecken
![]() hintereinander, die in den
Zeiten
hintereinander, die in den
Zeiten
![]() durchfahren werden?
durchfahren werden?
| Dieser Stoff wurde am 17.10.2001 behandelt |
Was bedeutet das, wenn wir (18. Jahrhundert) von Ulm nach Buchhorn (103 km, Durlesbach (-36 km (wir wandern zurück) , 9h) wandern?
Ulm, Durlesbach und Buchhorn liegen auf einem Kreissegment, also auf einer ''Linie''. Also ist die Durchschnittsgeschwindigkeit
Der Sprachgebrauch im Alltag sagt:
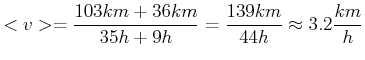 |
(3.18) |
Es wurde mit den Beträgen gerechnet.
| Wir verwenden ausschliesslich die physikalische Definition nach Gleichung (3.5) und Gleichung (3.6) ! |
![\includegraphics[width=0.8\textwidth]{Bilder/Bewegung-fahrplan.eps}](img109.gif)
|
| Dieser Stoff wurde am 17.10.2001 behandelt |
Momentangeschwindigkeit
![]() Tangente
Tangente
![]() Ableitung
Ableitung
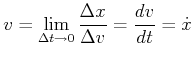 |
(3.19) |
![\includegraphics[width=0.5\textwidth]{Bilder/bewegung-ableitung.eps}](img112.gif)
|
Beispiel
Sei
![]() . Dann ist
. Dann ist
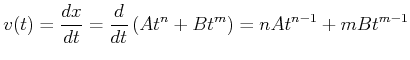 |
(3.20) |
Beschleunigung
![]() Änderung der Momentangeschwindigkeit
Änderung der Momentangeschwindigkeit
Mittlere Beschleunigung
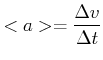 |
(3.21) |
Momentanbeschleunigung
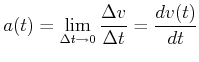 |
(3.22) |
Beschleunigung und Ort
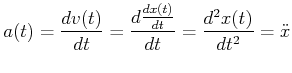 |
(3.23) |
Wie kommt man von einer bekannten Beschleunigung zum Ort?
![]() Integration
Integration
![\includegraphics[width=0.5\textwidth]{Bilder/bewegung-integration.eps}](img120.gif)
|
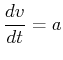 |
(3.24) |
| (3.25) |
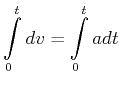 |
(3.26) |
| (3.27) |
| (3.28) |
Dabei ist die Anfangsbedingung mit eingerechnet.
Weg:
Wir integrieren auf beiden Seiten
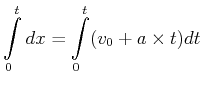 |
(3.30) |
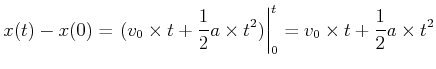 |
(3.31) |
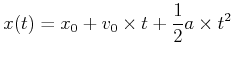 |
(3.32) |
| Schauen Sie in einem Mathematikbuch oder (Siehe Tipler, Physik[Tip94, 30]) nach, wie die Integration durchgeführt wird |
Materialien
Gleichung (3.18) kann verstanden werden, in dem man realisiert, dass die Geschwindigkeit sich von
![]() nach
nach ![]() ändert, so dass
ändert, so dass
![]() ist.
ist.
Gleichungen bei konstanter Beschleunigung
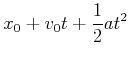 |
(3.33) |
Durchschnittsgeschwindigkeit
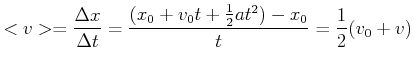 |
(3.34) |
Wenn die Endgeschwindigkeit
![]() ist, erhält man aus
ist, erhält man aus
![]() mit
mit
![]()