| Dieser Stoff wurde am 30.10.2001 behandelt |
Wir setzen voraus, dass wir alle Kräfte kennen: dann können wir die Beschleunigung und damit auch die bewegung eines Teilchens bestimmen.
| Dieser Stoff wurde am 30.10.2001 behandelt |
Erfahrung: wenn man versucht, ein Möbelstück zu verschieben, muss man eine Kraft ausüben.
| Reibungskräfte versuchen, Bewegungen zu verhindern oder zu dämpfen |
Beobachtung: Wenn ein Körper mit der Kraft ![]() , der Normalkraft, auf einen anderen Körper gedrückt
wird, wird mindestens eine Kraft
, der Normalkraft, auf einen anderen Körper gedrückt
wird, wird mindestens eine Kraft
| (4.74) |
benötigt, um den Körper in Bewegung zu setzen. ![]() heisst Haftreibungskraft.
heisst Haftreibungskraft. ![]() ist
der Haftreibungskoeffizient.
ist
der Haftreibungskoeffizient.
Umgekehrt gilt die Aussage, dass wenn die zur Auflagefläche parallele Kraft ![]() ist, bewegt sich
der Körper nicht. Die Haftreibungskraft, englisch: stiction, ist eines der grössten Probleme in der
Mikrosystemtechnik (englisch Micro-Electro-Mechanical-Systems, MEMS) und in der Festplattenindustrie.
ist, bewegt sich
der Körper nicht. Die Haftreibungskraft, englisch: stiction, ist eines der grössten Probleme in der
Mikrosystemtechnik (englisch Micro-Electro-Mechanical-Systems, MEMS) und in der Festplattenindustrie.
Wenn ein Körper gleitet, dann gilt die Beziehung
| (4.75) |
wobei ![]() dieGleitreibungskraft und
dieGleitreibungskraft und ![]() der Gleitreibungskoeffizient ist.
der Gleitreibungskoeffizient ist.
![\includegraphics[width=0.7\textwidth]{Bilder/PI_reibung_1.eps}](img315.gif)
Schematische Darstellung der Haft- und Gleitreibungskraft als Funktion der angelegten, parallel
zur Auflage wirkenden Kraft.
|
Schematisch verhalten sich Haftreibungskraft und Gleitreibungskraft wie in der Abbildung gezeigt.
![\includegraphics[width=0.8\textwidth]{Bilder/PI_reibung_2.eps}](img321.gif)
Kräfte auf einen Körper auf einer schiefen Ebene. Die x-Achse sei parallel zur Auflage, die y-Achse senkrecht dazu.
|
| (4.76) |
| (4.77) |
Oder
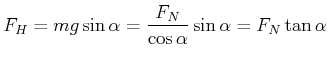 |
(4.78) |
Der Haftreibungskoeffizient ist gleich dem Tangens des Winkels, bei dem der Körper zu gleiten beginnt.
| (4.79) |
Gleitreibung wird durch Messung der Beschleunigung bestimmt.
| (4.80) |
| (4.81) |
oder
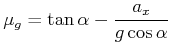 |
(4.82) |
| Dieser Stoff wurde am 30.10.2001 behandelt |
![\includegraphics[width=0.5\textwidth]{Bilder/PI_reibung_3.eps}](img329.gif)
Rollendes Rad:
rot gestrichelt: Geschwindigkeitsvektoren von der Achse aus gesehen (mitbewegt); grün:
Geschwindigkeitsvektor der Achse; blau: Summe.
|
Ein Rad, das am Boden abrollt, wird durch die Haftreibung zum drehen gebracht. Der momentane Drehpunkt eines Rades ist die Auflagefläche. Dies ist einfach ersichtlich, wenn die Geschwindigkeitsvektoren des Rades von der Achse aus gesehen (rot gestrichelt) zum Geschwindigkeitsvektor der Achse (grün) dazugezählt werden. Die resultierenden Geschwindigkeitsvektoren sind so, dass am Auflagepunkt die Geschwindigkeit gleich null ist. Da der Ort mit der Geschwindigkeit 0 immer die momentane Drehachse ist, dreht sich jedes abrollende Rad und jeder abrollende Körper um seinen Auflagepunkt.
Rollreibung meint die Reibung, die bei einem rollenden Körper auftritt. Ist der Körper nicht deformierbar, dann ist die Rollreibung null, wenn die beiden Oberflächen sich nicht anziehen (Adhäsion, Klebrigkeit!)
Die Zentripetalbeschleunigung ist
![]() . Die Masse des Autos sei
. Die Masse des Autos sei ![]() , der
Haftreibungskoeffizient
, der
Haftreibungskoeffizient ![]() . Dann muss
. Dann muss
![]() sein. Die
Geschwindigkeit muss der Bedingung
sein. Die
Geschwindigkeit muss der Bedingung
| (4.83) |
genügen. Die Zeit zum Durchfahren eines Bogens der Länge
![]() mit dem Winkel
mit dem Winkel ![]() im
Bogenmass und dem Radius
im
Bogenmass und dem Radius ![]() ist
ist
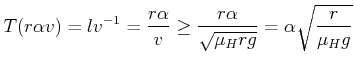 |
(4.84) |
| Dieser Stoff wurde am 31.10.2001 behandelt |
Materialien
Folien zur Vorlesung am 31. 10. 2001 PDF
Um die Bewegung eines Massenpunktes oder eines Systems von Massenpunkten zu berechnen, müssen die Bewegungsgleichungen gelöst werden. Das Prinzip von d'Alembert sagt:
| Ersetzt man bei einem bewegten System von Massenpunkten so hat man das dynamische Problem formal auf ein statisches Problem zurückgeführt. |
![\includegraphics[width=0.47\textwidth]{Bilder/bewegung_dAlembert1.eps}](img338.gif)
![\includegraphics[width=0.4\textwidth]{Bilder/bewegung_dAlembert2.eps}](img339.gif)
Prinzip von d'Alembert. Links der Standpunkt eines ruhenden Beobachters, rechts derjenige des mitbewegten
Beobachters. Die
|
Beschreibung durch den ruhenden Beobachter mit dem 2. Newtonschen Axiom (Dynamik)
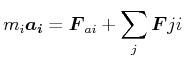 |
(4.85) |
Und nun die Beschreibung des mitbewegten Beobachters (Für ihn ist der Schwerpunkt des Massensystems in Ruhe!).
Nach d'Alembert gilt
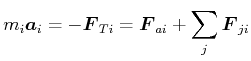 |
(4.86) |
und damit die Beschreibung im mitbewegten Bezugssystem (Statik) über das formale Kräftegleichgewicht
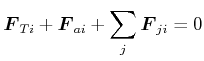 |
(4.87) |
| Dieser Stoff wurde am 31.10.2001 behandelt |
![\includegraphics[width=0.7\textwidth]{Bilder/bewegung-tisch.eps}](img345.gif)
Zwei verbundene Körper an einem Tisch.
|
Masse 1 wird beschleunigt. Trägheitskraft
![]() (Seilspannung)
(Seilspannung)
Masse 2 wird beschleunigt. Kräfte an Masse 2: Trägheitskraft
![]() sowie Erdbeschleunigung
sowie Erdbeschleunigung
![]() . Die resultierende Kraft ist die Seilspannung
. Die resultierende Kraft ist die Seilspannung
![]() .
.
Nun muss ![]() für beide Massen gleich sein (dehnungsfreies Seil). Ebenso ist die Seilspannung
überall gleich.
für beide Massen gleich sein (dehnungsfreies Seil). Ebenso ist die Seilspannung
überall gleich.
| (4.88) |
oder
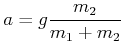 |
(4.89) |
und die Seilspannung
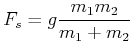 |
(4.90) |
![\includegraphics[width=0.95\textwidth]{Bilder/bewegung-2massen.eps}](img354.gif)
Beschleunigung zweier aufeinanderliegender Massen.
|
Wir betrachten nun die untere Masse als bewegt.
Wenn die Grenzkraft der Haftreibungskraft nicht überschritten wird, wenn also
![]() ist, bewegen sich die beiden Körper zusammen. Die Haftreibungskraft
ist, bewegen sich die beiden Körper zusammen. Die Haftreibungskraft
![]() kann eliminiert werden.
kann eliminiert werden.
| (4.91) |
Hier ist
![]() der Haftreibungskoeffizient zwischen den Massen 1 und 2 und
der Haftreibungskoeffizient zwischen den Massen 1 und 2 und
![]() der Haftreibungskoeffizient zwischen der Masse 2 und der Unterlage.
der Haftreibungskoeffizient zwischen der Masse 2 und der Unterlage.
Wenn die durch die Trägheit der Masse 1 generierte Kraft grösser als die maximale Haftreibungskraft ist, dann gleitet Masse 1 auf Masse 2. Dies tritt nicht auf, wenn
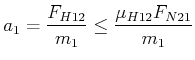 |
(4.92) |
ist. Dies ist äquivalent zu
| (4.93) |
| (4.94) |
Gleitet Masse 1 über Masse 2, dann ist die übertragene Kraft
![]() die
Gleitreibungskraft mit
die
Gleitreibungskraft mit ![]() dem Gleitreibungskoeffizienten zwischen den beiden Massen. Das horizontale
Kräftegleichgewicht für die Masse 2 muss nun für beide Grenzflächen mit den Gleitreibungskoeffizienten
geschrieben werden.
dem Gleitreibungskoeffizienten zwischen den beiden Massen. Das horizontale
Kräftegleichgewicht für die Masse 2 muss nun für beide Grenzflächen mit den Gleitreibungskoeffizienten
geschrieben werden.
Die Masse 1 wird mit
| (4.95) |
beschleunigt; die Masse 2 mit
| (4.96) |
Also ist
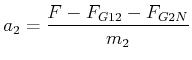 |
(4.97) |
Bemerkung: Wenn
![]() ist, ist es nicht möglich die Masse 2 in Bewegung zu setzen ohne dass Masse 1
gleitet!
ist, ist es nicht möglich die Masse 2 in Bewegung zu setzen ohne dass Masse 1
gleitet!
| Dieser Stoff wurde am 31.10.2001 behandelt |
Fallbewegung in einem bewegten Wagen. Der Wagen wird genau ab dem Moment beschleunigt, ab dem auch der Ball zu fallen beginnt.
![\includegraphics[width=0.7\textwidth]{Bilder/bewegung-bezugsystem1.eps}](img376.gif)
Standpunkt eines ruhenden Beobachters: Fall in einem beschleunigten Wagen.
|
Für den ruhenden Fällt der Ball ganz gewöhnlich. Für ihn ist ![]() die Ursache der Bewegung.
die Ursache der Bewegung.
![\includegraphics[width=0.7\textwidth]{Bilder/bewegung-bezugsystem2.eps}](img378.gif)
Standpunkt eines mitbewegten Beobachters: Fall in einem beschleunigten Wagen.
|
Für den mitbewegten Beobachter sieht das ganze anders aus. Auf den Ball scheint für ihn die Kraft
![]() zu wirken. Auf den Ball wirkt vom beschleunigten Beobachter aus gesehen eine
zusätzliche Kraft
zu wirken. Auf den Ball wirkt vom beschleunigten Beobachter aus gesehen eine
zusätzliche Kraft ![]() , die in einem Inertialsystem nicht wirkt. Diese von einem ruhenden
Beobachter aus nicht vorhandene Kraft wird deshalb auch Scheinkraft genannt. Der Begriff ist schlecht, da
für den mitbewegten Beobachter die Kraft
, die in einem Inertialsystem nicht wirkt. Diese von einem ruhenden
Beobachter aus nicht vorhandene Kraft wird deshalb auch Scheinkraft genannt. Der Begriff ist schlecht, da
für den mitbewegten Beobachter die Kraft ![]() sehr real ist. Der mitbewegte (beschleunigte)
Beobachter muss die Scheinkraft
sehr real ist. Der mitbewegte (beschleunigte)
Beobachter muss die Scheinkraft
![]() einführen, um die Newtonschen Axiome zu retten (diese
gelten nach der Definition eigentlich nicht in einem beschleunigten Bezugssystem).
einführen, um die Newtonschen Axiome zu retten (diese
gelten nach der Definition eigentlich nicht in einem beschleunigten Bezugssystem).
![\includegraphics[width=0.7\textwidth]{Bilder/bewegung-bezugsystem-lampe.eps}](img382.gif)
In einem beschleunigten Wagen hängende Lampe. Links der Standpunkt eines beschleunigten Beobachters, rechts der Standpunkt des mitbeschleunigten Beobachters.
|
Für beide, den ruhenden und den mitbeschleunigten Beobachter ist die Seilspannung im Seil, das die Lampe hält, sowie das Gewicht der Lampe das gleiche. Die Interpretation ist aber verschieden.
(Siehe Tipler, Physik[Tip94, 116])
Wir betrachten ein rotierendes Bezugsystem. Eine Masse ![]() ist an einer Schnur an der Achse
verbunden.
ist an einer Schnur an der Achse
verbunden.
| Dieser Stoff wurde am 31.10.2001 behandelt |
|
[width=0.7]Bilder/bewegung-bezugsystem-coriolis.eps Bewegung eines von einer rotierenden Scheibe geworfenen Balls. Links der Standpunkt des ruhenden Beobachters. Rechts derjenige des mitbewegten Beobachters. (Für diesen rotiert die Welt, analog dazu dass für uns die sonne sich bewegt!)
|
Rotierende Bezugssysteme können mit der Zentrifugalkraft alleine nicht beschrieben werden. Da bei gleicher Winkelgeschwindigkeit die lineare Geschwindigkeit vom Abstand zur Drehachse abhängt, muss eine den Abstand zur Drehachse ändernde Bewegung notwendigerweise eine beschleunigte Bewegung sein. Diese Im rotierenden Bezugssystem auftretende Beschleunigung, die immer senkrecht zur Geschwindigkeit steht und verschwindet, wenn die Geschwindigkeit null ist, heisst die Coriolis-Beschleunigung.
Die Coriolis-Beschleunigung und Coriolis-Kraft sind für die lange Lebensdauer der Hochdruckgebiete und Tieftruckgebiete verantwortlich.
| Dieser Stoff wurde am 31.10.2001 behandelt |
Wie berechnet man eine Bahnkurve, wenn man die Kraft (Beschleunigung) gegeben ist? Diese Frage ist die gleich wie die Frage nach der Methode zum Lösen von Differenzialgleichungen.
Mit
Wir können die Geschwindigkeit zur Zeit ![]() folgendermassen berechnen:
folgendermassen berechnen:
| (4.98) |
Die Geschwindigkeit zur Zeit ![]() ist
ist
| (4.99) |
Analoge Gleichungen gelten für den Ort.
Zusammen erhalten wir das Euler-Verfahren.
| (4.100) |
|
[width=0.7]Bilder/bewegung-euler.eps
Beispiel des Euler-Verfahrens mit
|