Weiter: Schwerkraft oder Gravitation Oben: Dynamik, die Newtonschen Axiome Zurück: Drehbewegungen  Skript:  PDF-Datei Übungen:  Blätter

Unterabschnitte

• Schwerpunkt
  • Beispiele für statisches Gleichgewicht
• Kräftepaare
• Stabilität des Gleichgewichts

Statische Gleichgewichte von starren Körpern

Dieser Stoff wurde am 27.11.2001 behandelt

(Siehe Tipler, Physik[Tip94, 279])

Starre Körper sind im Gleichgewicht, wenn

$$\sum \vec{F}_{extern} = 0$$ (4.315)

und wenn

$$\sum\vec{M}_{extern} = 0$$ (4.316)

Schwerpunkt

Dieser Stoff wurde am 27.11.2001 behandelt

(Siehe Tipler, Physik[Tip94, 281])

Das Drehmoment auf einen Körper kann wie folgt behandelt werden:

Auf jedes Massenelement wirkt die Kraft $\vec{F}_i = m_i \vec{g}$. Wir vereinfachen das Problem und betrachten eine Massenverteilung entlang der x-Achse. Wenn der Drehpunkt $x_0$ wäre, dann wäre das resultierende Drehmoment

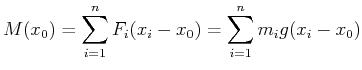$$M(x_0) = \sum\limits_{i=1}^n F_i (x_i-x_0) = \sum\limits_{i=1}^n m_i g (x_i-x_0)$$ (4.317)

Wir suchen $x_0$ so, dass $M(x_0)=0$ ist. Dann gilt

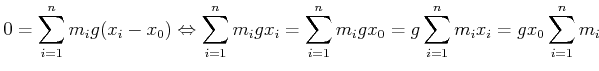$$0 = \sum\limits_{i=1}^n m_i g (x_i-x_0) \Leftrightarrow \sum\limi... ...=1}^n m_i g x_0 = g \sum\limits_{i=1}^n m_i x_i = g x_0 \sum\limits_{i=1}^n m_i$$ (4.318)

Damit haben wir die Definition des Massenmittelpunktes aufgeschrieben.

In einem homogenen Kraftfeld ist der Schwerpunkt (über das Drehmoment definiert) identisch mit dem Massenmittelpunkt.

In drei Dimensionen lautet die entsprechende Gleichung:

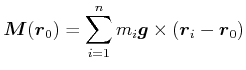$$\vec{M}(\vec{r}_0) = \sum\limits_{i=1}^n m_i \vec{g}\times (\vec{r}_i -\vec{r}_0)$$ (4.319)

Daraus folgt mit einer analogen Überlegung, dass

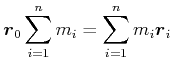$$\vec{r}_0 \sum\limits_{i=1}^n m_i = \sum\limits_{i=1}^n m_i \vec{r}_i$$ (4.320)

Als Integral geschrieben

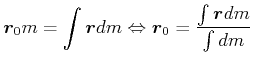$$\vec{r}_0 m = \int \vec{r}dm \Leftrightarrow \vec{r}_0 = \frac{\int \vec{r}dm}{\int dm}$$ (4.321)

Beispiele für statisches Gleichgewicht

Dieser Stoff wurde am 27.11.2001 behandelt

(Siehe Tipler, Physik[Tip94, 283])

Kräfte an einem Arm

Es gilt

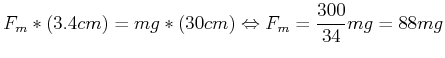$$F_m * ( 3.4 cm) = mg * (30 cm) \Leftrightarrow F_m = \frac{300}{34} mg = 88 mg$$ (4.322)

Für eine Masse von 10 kg ergibt sich also $F_M \approx 8.8 kN$.

Kräfte bei einer Leiter

Da die Leiter sich nicht bewegt, müssen die Kräfte in horizontaler Richtung und die Kräfte in vertikaler Richtung sich aufheben.

$$F_N = F_G$$

$$F_H = F_1$$ (4.323)

Die Verknüpfung der horizontalen und vertikalen Kräfte wird durch die Bedingung, dass die Leiter sich nicht dreht, bewirkt. Wir sind frei in der Wahl des Drehpunktes und wählen den Fusspunkt als Drehpunkt. Dann sind die Hebelarme von $F_H$ und $F_N$ null, diese Kräfte müssen also nicht betrachtet werden.

$$F_g \cdot \ell_S = F_1 \cdot h$$ (4.324)

Die Leiter steht dann fest, wenn $F_H \leq \mu_H F_N$ ist. Diese Gleichung kann auch als

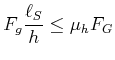$$F_g \frac{\ell_S}{h} \leq \mu_h F_G$$ (4.325)

ist. Der Haftreibungskoeffizient muss also mindestens

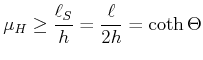$$\mu_H \geq \frac{\ell_S}{h} = \frac{\ell}{2h} = \coth\Theta$$ (4.326)

sein ($\Theta$ ist der Neigungswinkel).

Kräftepaare

Dieser Stoff wurde am 27.11.2001 behandelt

(Siehe Tipler, Physik[Tip94, 287])

Eine an einem beliebigen Ort angreifende Kraft kann durch die Addition der Kraft ''0'' am Schwerpunkt in eine dort angreifende Kraft und ein reines Drehmoment übergeführt werden.

Ursprünglich wirkt nur die ausserhalb des Schwerpunktes angreifende Kraft $\vec{F}$. Durch die Addition der Kräfte $\vec{F}$ (blau) und $-\vec{F}$ (rot) im Schwerpunkt ändert sich die netto-äussere Kraft nicht. Wir lassen nun die blaue Kraft $\vec{F}$ am Schwerpunkt wirken und betrachten das Drehmoment der im Schwerpunkt angreifenden Kraft $-\vec{F}$ und der ursprünglichen Kraft $\vec{F}$ (grün) bezüglich eines beliebigen Punktes $\vec{r}_0$. Der Ortsvektor des ersten Punktes sei $\vec{r}_1$ und der Ortsvektor des Schwerpunktes $\vec{r}_S$. Dann ist $\vec{r}= \vec{r}_1 - \vec{r}$. Wir haben

$$\vec{M} = \vec{F}\times (\vec{r}_1 - \vec{r}_0) + (-\vec{F})\times (\vec{r}_S -\vec{R}_0)$$

$$= \vec{F}\times (\vec{r}_1 -\vec r_0 - (\vec {r}_S -\vec {r}_0))$$

$$= \vec {F} \times (\vec {r}_1 - \vec {r}_S) = \vec {F} \times \vec {r}$$ (4.327)

Das Kräftepaar entspricht einem reinen Drehmoment! Die Grösse des Drehmomentes ist für jeden Raumpunkt $\vec {r}_0$ gleich.

r_0 - (boldsymbolr_S -boldsymbolr_0))
&=& boldsymbolF ×(boldsymbolr_1 - boldsymbolr_S) = boldsymbolF ×boldsymbolr

Stabilität des Gleichgewichts

Dieser Stoff wurde am 27.11.2001 behandelt

(Siehe Tipler, Physik[Tip94, 289])

Für die Stabilität des Gleichgewichtes gelten die gleichen Regeln wie für die Minima der potentiellen Energie. Wenn die Auslenkung eines Körpers aus seiner Ruhelage eine Kraft oder ein Drehmoment bewirkt, das diesen in die Ruhelage zurücktreibt, spricht man von einem stabilen Gleichgewicht. Im entgegengesetzten Fall handelt es sich um ein labiles Gleichgewicht. Eine Kugel auf einer horizontalen Unterlage befindet sich in einem indifferenten Gleichgewicht.

 Skript:  PDF-Datei Übungen:  Blätter