![\includegraphics[width=0.8\textwidth]{kepler2.eps}](img991.gif)
2. Keplersches Gesetz
| Dieser Stoff wurde am 27.11.2001 behandelt |
Die Schwerkraft oder Gravitation ist die einzige langreichweitige Kraft (soweit wir wissen), die sich nicht kompensiert. In diesem Kapitel sollen Aspekte der Gravitation besprochen werden. Einige der Diskussionspunkte sind auch für die Behandlung der elektrostatischen Felder von Bedeutung.
| Dieser Stoff wurde am 27.11.2001 behandelt |
Die Keplerschen Gesetze lauten
|
![\includegraphics[width=0.8\textwidth]{kepler2.eps}](img991.gif)
2. Keplersches Gesetz
|
Das zweite Keplersche Gesetz drückt die Drehimpulserhaltung aus. Diese besagt, dass in einem abgeschlossenen
System
![]() gilt. In den Zylinderkoordinaten
gilt. In den Zylinderkoordinaten
![]() lautet der Satz der Drehimpulserhaltung
lautet der Satz der Drehimpulserhaltung
![]() Für eine sehr kurze Zeit
Für eine sehr kurze Zeit ![]() gilt
gilt
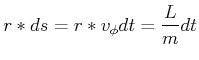 |
(4.328) |
und damit der Flächensatz.
Materialien
Folien zur Vorlesung am 28. 11. 2001 PDF
| Dieser Stoff wurde am 28.11.2001 behandelt |
Aus der Umlaufszeit des Mondes von 27.3 Tagen kann mit der Formel für die Zentripetalbeschleunigung
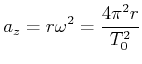 |
(4.329) |
die Gravitationskraft auf der Mondbahn
![]() ausgerechnet werden.
ausgerechnet werden.
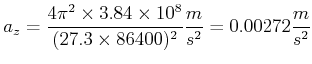 |
(4.330) |
Auf der Erdoberfläche (
![]() )ist
)ist
![]() . Wenn wir annehmen, dass sich die
Gravitationsbeschleunigung wie
. Wenn wir annehmen, dass sich die
Gravitationsbeschleunigung wie
![]() verhält, dann ist
verhält, dann ist
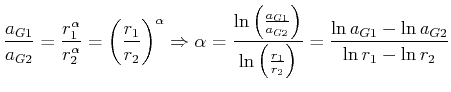 |
(4.331) |
Wir setzen ein und erhalten
![]() , also ein Gravitationsgesetz der Form
, also ein Gravitationsgesetz der Form
![]() .
.
Neben dieser Beobachtung, die unabhängig von den Keplerschen Sätzen ist, kann man auch aus diesen die Form des Gravitationsgesetzes abgeleiten.
Da die Gravitation die einzige Möglichkeit für die ursächliche Kraft der Zentripetalbeschleunigung
ist, muss
![]() sein. Das 3. Keplersche Gesetz sagt nun dass
sein. Das 3. Keplersche Gesetz sagt nun dass
![]() ist. Wir haben also
ist. Wir haben also
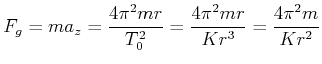 |
(4.332) |
Das heisst, dass nach dem 3. Keplerschen Gesetz die Gravitationskraft
![]() sein muss.
sein muss.
Wir verwenden das 1. und das 2. Keplersche Gesetz.
![\includegraphics[width=0.6\textwidth]{ellipse.eps}](img1009.gif)
Parameter bei einer Ellipse. Die Ellipse ist definiert, dass die Summe der Abstände von jedem Punkt
ihrer Berandung zu den beiden Brennpunkten konstant und gleich dem grossen Durchmesser
|
Wir nehmen an, dass die Bahn ![]() eines Teilchens ganz allgemein durch
eines Teilchens ganz allgemein durch ![]() gegeben ist. Dann
schreiben wir die Geschwindigkeit in einem Zylinderkoordinatensystem als
gegeben ist. Dann
schreiben wir die Geschwindigkeit in einem Zylinderkoordinatensystem als
![]() . Der
Drehimpuls ist in diesem Koordinatensystem durch
. Der
Drehimpuls ist in diesem Koordinatensystem durch
![]() gegeben. Damit ist auch
gegeben. Damit ist auch
![]() und
und
![]() .
.
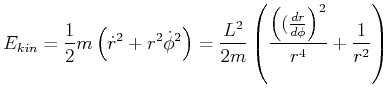 |
(4.333) |
Die Gesamtenergie bestehend aus der kinetischen Energie und einer unbekannten potentiellen Energie
![]() muss konstant sein.
muss konstant sein.
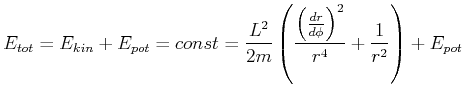 |
(4.334) |
Das erste Keplersche Gesetz sagt aus, dass die Bahnen Ellipsen sind. Wir verallgemeinern auf Kegelschnitte und bemerken, dass alle Kegelschnitte (Hyperbel, Parabel und Ellipse) in Zylinderkoordinaten durch die Gleichung
 |
(4.335) |
gegeben sind, wobei ![]() der Winkel des Ortsvektors zur grossen Halbachse ist. Wir haben dann
der Winkel des Ortsvektors zur grossen Halbachse ist. Wir haben dann
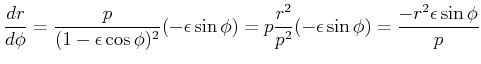 |
(4.336) |
Mit dieser Gleichung kann
![]() berechnet werden
berechnet werden
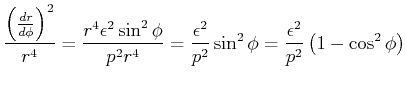 |
(4.337) |
Weiter ist
![]() und damit
und damit
![]() . Somit wird
. Somit wird
![$\displaystyle \frac{\left(\frac{dr}{d\phi}\right)^2}{r^4} = \frac{\epsilon^2}{p...
...{1}{\epsilon^2}\right] = \frac{\epsilon^2-1}{p^2} + \frac{2}{pr} -\frac{1}{r^2}$](img1025.gif) |
(4.338) |
Eingesetzt in die kinetische Energie ![]() erhalten
wir
erhalten
wir
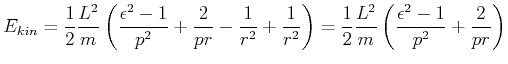 |
(4.339) |
Damit die Gesamtenergie konstant ist, muss die potentielle Energie
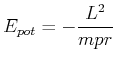 |
(4.340) |
sein.
Weiter ist es, bei einer Annahme von linearen Systemen, natürlich, dass die Gravitationskraft proportional zu den beteiligten Massen ist.
Aus all diesen Beobachtungen hat Newton sein Gravitationsgesetz abgeleitet.
Der Vektor
![]() ist ein Einheitsvektor, der von der Masse
ist ein Einheitsvektor, der von der Masse ![]() zur Masse
zur Masse ![]() zeigt. Dieser Vektor definiert das Vorzeichen der Kraft!
zeigt. Dieser Vektor definiert das Vorzeichen der Kraft!
Aus der Gravitationskraft kann die potentielle Energie der Gravitation berechnet werden, indem wir von einem Ort ![]() auf dem Strahl vom Koordinatenursprung
(Ort der Masse
auf dem Strahl vom Koordinatenursprung
(Ort der Masse ![]() ins unendliche integrieren.
ins unendliche integrieren.
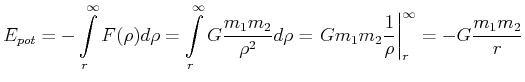 |
(4.342) |
Was wir bis jetzt berechnet haben, ist die Arbeit von die benötigt wird, um eine Masse ![]() im Feld der
Masse
im Feld der
Masse ![]() ins Unendliche zu verschieben. Wir müssen zeigen, dass diese Arbeit unabhängig vom Weg ist. Jede
allgemeine Verschiebung kann als eine Kombination einer radialen Verschiebung sowie einer zweiten
Verschiebung in konstantem Abstand zur Masse
ins Unendliche zu verschieben. Wir müssen zeigen, dass diese Arbeit unabhängig vom Weg ist. Jede
allgemeine Verschiebung kann als eine Kombination einer radialen Verschiebung sowie einer zweiten
Verschiebung in konstantem Abstand zur Masse ![]() geschrieben werden. Bei der Verschiebung auf einer
Kugelschale (konstanter Abstand) ist die Kraft immer senkrecht auf der Verschiebung, die Arbeit also
null. Das heisst, dass nur die Abstandsänderung zur Arbeit beiträgt, und diese ist gleich, unabhängig vom
Weg. Deshalb ist das Gravitationsfeld ein konservatives Kraftfeld.
geschrieben werden. Bei der Verschiebung auf einer
Kugelschale (konstanter Abstand) ist die Kraft immer senkrecht auf der Verschiebung, die Arbeit also
null. Das heisst, dass nur die Abstandsänderung zur Arbeit beiträgt, und diese ist gleich, unabhängig vom
Weg. Deshalb ist das Gravitationsfeld ein konservatives Kraftfeld.
Aus der potentiellen Energie können wir die Kraft nach
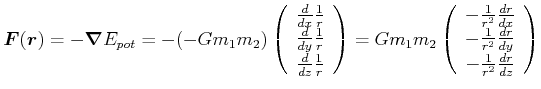 |
(4.343) |
Wir beachten, dass
![]() ist. Dann ist
ist. Dann ist
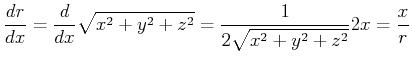 |
(4.344) |
Also ist
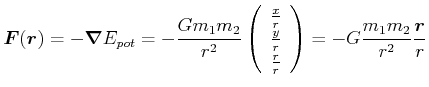 |
(4.345) |
Oft ist es sinnvoll, die von der Masse ![]() ausgehende Kraftwirkung unabhängig von der Masse
ausgehende Kraftwirkung unabhängig von der Masse ![]() anzugeben. Wir definieren deshalb:
anzugeben. Wir definieren deshalb:
Der Feldvektor des Gravitationsfeldes ist
|
An der Erdoberfläche ist der Betrag des Feldvektors der Gravitation
![]() (stimmt das?).
(stimmt das?).
![\includegraphics[width=0.5\textwidth]{gravitationsfeld.eps}](img1040.gif)
Das Gravitationsfeld
|
Wir können für das Gravitationsfeld Feldlinien einzeichnen. Eine Probemasse wird durch das Gravitationsfeld beschleunigt und bewegt sich entlang der Feldlinien. Das Gravitationsfeld verhält sich analog zum elektrostatischen Feld.
In der Nähe der Erdoberfläche ![]() können wir die potentielle
Energie linearisieren.
können wir die potentielle
Energie linearisieren.
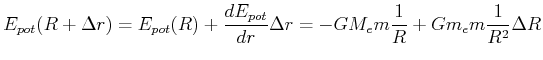 |
(4.347) |
Wenn wir den Nullpunkt der potentiellen Energie auf die Erdoberfläche legen, haben wir
![$\displaystyle E_{pot}(R+\Delta r) - E_{pot}(R) = G m_e m \frac{1}{R^2} \Delta R = m \left[ G m_e \frac{1}{R^2}\right] \Delta R = m g \Delta R$](img1043.gif) |
(4.348) |
indem wir
![]() setzen.
setzen.
| Die Formel
|
Analog zum klassischen Elektronenradius könnte man sich fragen, bei welchem Radius die
Gravitationsenergie der Erde gleich der Energie ![]() ist. Wir setzen
ist. Wir setzen
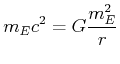
und erhalten
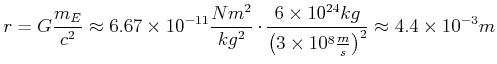
| Dieser Stoff wurde am 28.11.2001 behandelt |
Durch die Bestimmung der Umlaufzeiten und Umlaufbahnen von Himmelskörpern kann immer nur das Verhältnis zweier Massen, nie aber der Absolutwert bestimmt werden. Deshalb müssen zwei Testmassen in einen kontrollierten Abstand gebracht werden.
![\includegraphics[width=0.5\textwidth]{gravitationswaage.eps}](img1049.gif)
Abbildung der Gravitationswaage aus der Vorlesungssammlung.
|
Die Gravitationswaage ist symmetrisch aufgebaut, um Fehler zu minimieren und um den Effekt zu verdoppeln. Gemessen wird die Winkelbeschleunigung
| Dieser Stoff wurde am 4.12.2001 behandelt |
Materialien
Übungsblatt 8 vom 04. 12. 2001 (HTML oder PDF)
Folien zur Vorlesung am 04. 12. 2001 PDF
Wir haben bis jetzt immer angenommen (und bei der Beschleunigungsmethode (Gleichung (4.257) ),
die wir angewandt hatten, tun wir dies auch), dass die träge Masse ![]() (der
Proportionalitätsfaktor im 2. Newtonschen Axiom) gleich der schweren Masse
(der
Proportionalitätsfaktor im 2. Newtonschen Axiom) gleich der schweren Masse ![]() im
Gravitationsgesetz sei. Gleichung (4.257) müsste eigentlich lauten
im
Gravitationsgesetz sei. Gleichung (4.257) müsste eigentlich lauten
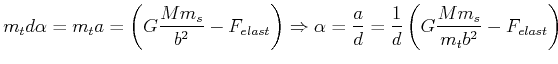 |
(4.350) |
| Dieser Stoff wurde am 4.12.2001 behandelt |
Mit der üblicherweise verwendeten Notation, dass
![]() sei, berechnet man sofort, dass es unmöglich
sein sollte, die Erde zu verlassen. Wir starten an der Erdoberfläche und setzen
sei, berechnet man sofort, dass es unmöglich
sein sollte, die Erde zu verlassen. Wir starten an der Erdoberfläche und setzen ![]() und möchten, unter
Vernachlässigung der Reibung bis in den Abstand
und möchten, unter
Vernachlässigung der Reibung bis in den Abstand ![]() kommen. Die dafür nötige kinetische
Energie ist
kommen. Die dafür nötige kinetische
Energie ist
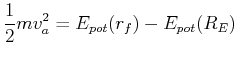 |
|||
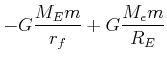 |
|||
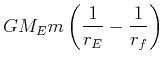 |
|||
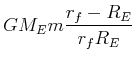 |
(4.351) |
Daraus ergibt sich
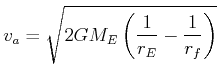 |
(4.352) |
Wenn wir
![]() setzen, berechnen wir, dass
setzen, berechnen wir, dass
![]() ist. Die Geschwindigkeit auf
einer Umlaufbahn in der Höhe
ist. Die Geschwindigkeit auf
einer Umlaufbahn in der Höhe ![]() können wir mit der Zentripetalbeschleunigung ausrechnen:
können wir mit der Zentripetalbeschleunigung ausrechnen:
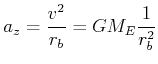 |
(4.353) |
Daraus folgt, dass
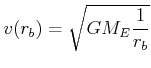 |
(4.354) |
ist.
| Dieser Stoff wurde am 4.12.2001 behandelt |
Die Umlaufgeschwindigkeit für ![]() ist
ist
![]() .
.
Die gesamte Energie eines Satelliten ist
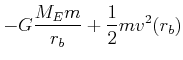 |
|||
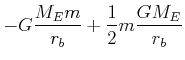 |
|||
 |
|||
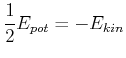 |
(4.355) |
Wenn wir eine bestimmte Umlaufsfrequenz vorgeben, also ![]() , dann Teilchen einen Drehimpuls
, dann Teilchen einen Drehimpuls
![]() . Seine kinetische Energie ist dann
. Seine kinetische Energie ist dann
![]() . Dies entspricht einer potentiellen Energie im
mitdrehenden Koordinatensystem
. Dies entspricht einer potentiellen Energie im
mitdrehenden Koordinatensystem
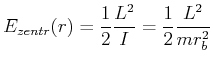 |
(4.356) |
Die gesamte Energie ist also
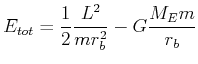 |
(4.357) |
Sie hat ein Minimum bei dem für den Drehimpuls charakteristischen Bahnabstand. Ellipsenbahnen können als ein Oszillieren in dieser Landschaft der potentiellen Energie angesehen werden.
![\includegraphics[width=0.6\textwidth]{zentripotential.eps}](img1078.gif)
Kombiniertes Gravitations-und Zentrifugalpotential
|