![\includegraphics[width=0.4\textwidth]{winkelgeschwindigkeit.eps}](img731.gif)
Winkel und Winkelgeschwindigkeit
| Dieser Stoff wurde am 14.11.2001 behandelt |
![\includegraphics[width=0.4\textwidth]{winkelgeschwindigkeit.eps}](img731.gif)
Winkel und Winkelgeschwindigkeit
|
| Dieser Stoff wurde am 14.11.2001 behandelt |
Wir betrachten einen Kreisbogen der Länge ![]() im Abstand
im Abstand ![]() von der Drehachse.
von der Drehachse.
Dann ist ![]() . Die dazugehörige Winkeländerung ist
. Die dazugehörige Winkeländerung ist
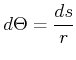 |
(4.242) |
ist unabhängig vom Abstand von der Drehachse.
Einheiten:
![]() .
.
|
|
Einheiten:
![]() . Die Drehfrequenz hängt mit der Winkelgeschwindigkeit über
. Die Drehfrequenz hängt mit der Winkelgeschwindigkeit über
![]() zusammen.
zusammen.
|
|
Einheit:
![]() .
.
Die Tangentialgeschwindigkeit ist eines Teilchens im Abstand ![]() ist
ist
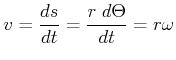 |
(4.243) |
Die tangentiale Beschleunigung ist
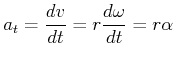 |
(4.244) |
Die Zentripetalbeschleunigung ist zum Mittelpunkt hin gerichtet und hat die Grösse
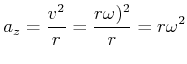 |
(4.245) |
Analog zu den Gesetzen der linearen Bewegung haben nwir
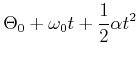 |
|||
| (4.246) |
| Dieser Stoff wurde am 20.11.2001 behandelt |
Materialien
Folien zur Vorlesung am 20. 11. 2001 PDF
Übungsblatt 6 vom 20. 11. 2001 (HTML oder PDF)
Welche Kräfte können eine Scheibe zum Drehen bringen?
Wir teilen die Scheibe in ![]() Teile. Auf das
Teile. Auf das ![]() -te Teilchen wirkt die Kraft
-te Teilchen wirkt die Kraft ![]() mit einem
Hebelarm
mit einem
Hebelarm
![]() , wobei
, wobei ![]() der Winkel zwischen der Kraft
der Winkel zwischen der Kraft ![]() und dem
Ortsvektor
und dem
Ortsvektor ![]() ist.
ist.
Das Drehmoment durch die Kraft ![]() ist also
ist also
| (4.247) |
wenn ![]() die Tangentialkomponente der Kraft
die Tangentialkomponente der Kraft ![]() ist.
ist.
| (4.248) |
Durch die Multiplikation dieser Gleichung mit ![]() erhält man
erhält man
| (4.249) |
Über alle Teilchen summiert, bekommt man
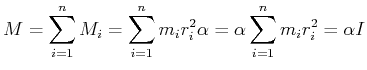 |
(4.250) |
|
ist das Trägheitsmoment. Es übernimmt für die Drehbewegungen die Funktion, die die Masse für Translationsbewegungen innehat. |
Also
| (4.252) |
Die Werte der Trägheitsmomente finden sie im Tipler[Tip94, 231].
Beispiel:
![\includegraphics[height=0.3\textheight]{drehmoment.eps}](img761.gif)
Ein Körper der Masse
|
An der Scheibe gilt die Drehmomentgleichung
| (4.253) |
Die Beschleunigung der Masse m ist
| (4.254) |
Das Seil impliziert die folgende Beziehung
| (4.255) |
Damit wird
| (4.256) |
Weiter erhält man
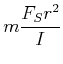 |
|||
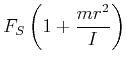 |
|||
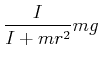 |
(4.257) |
Damit wird die Beschleunigung
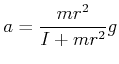 |
(4.258) |
Nun ist für eine Vollscheibe
![]() . Damit wird die Gleichung
. Damit wird die Gleichung
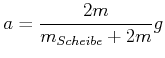 |
(4.259) |
| Dieser Stoff wurde am 20.11.2001 behandelt |
Wir betrachten ein rotierendes Objekt, das in ![]() Teile geteilt sei. Bei einer infinitesimalen
Drehung um
Teile geteilt sei. Bei einer infinitesimalen
Drehung um
![]() der Masse
der Masse ![]() , die sich im Abstand
, die sich im Abstand ![]() von der Drehachse befinde,
ist die Arbeit
von der Drehachse befinde,
ist die Arbeit
| (4.260) |
Aufsummiert erhält man
| (4.261) |
Die Leistung dieser Arbeit ist
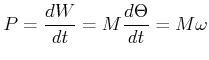 |
(4.262) |
Wir berechnen nun die Beschleunigungsarbeit für Drehungen, um zu einem Ausdruck für die kinetische Energie der Rotationsbewegung zu erhalten.
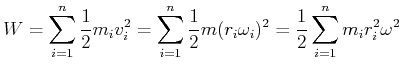 |
(4.263) |
| Dieser Stoff wurde am 20.11.2001 behandelt |
In Gleichung (4.161) wird die Summe durch ein Integral ersetzt.
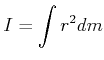 |
(4.264) |
Beispiel:
![\includegraphics[width=0.3\textwidth]{traegheit_ring.eps}](img786.gif)
Trägheitsmoment eines Kreisrings des Radius
|
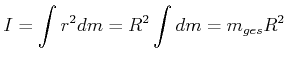 |
(4.265) |
Beispiel:
Trägheitsmoment ![]() eines Stabes entlang der x-Achse, Länge
eines Stabes entlang der x-Achse, Länge ![]() , der um die y-Achse rotiert
und dessen geamte Masse auf der x-Achse konzentriert ist.
, der um die y-Achse rotiert
und dessen geamte Masse auf der x-Achse konzentriert ist.
Massenelement
![]()
Beispiel:
Trägheitsmoment einer homogenen Scheibe, Radius ![]() .
.
Die auf einem Kreisring mit dem Radius r befindliche Masse ist
![]() ,
,
![]()
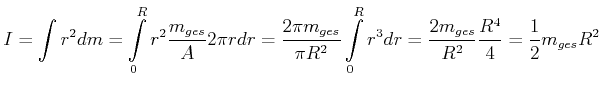 |
(4.267) |
Das Resultat für den Vollzylinder, der um seine Symmetrieachse rotiert, ist das gleiche.
Wenn ich einen Körper bilden kann, indem ich eine Grundform, von der ![]() bekannt ist, nehme und
eine zweite Form, von der
bekannt ist, nehme und
eine zweite Form, von der ![]() bekannt ist, subtrahiere (z.B. Hohlzylinder als Differenz zweier
Zylinder), dann ist das resultierende Trägheitsmoment
bekannt ist, subtrahiere (z.B. Hohlzylinder als Differenz zweier
Zylinder), dann ist das resultierende Trägheitsmoment
| (4.268) |
Wenn das Trägheitsmoment ![]() eines Körpers um eine bestimmte, durch den Schwerpunkt
gehende Drehachse bekannt ist, wenn aber der Körper um eine zu dieser Drehachse parallele Achse
rotiert, kann das neue Trägheitsmoment mit dem Satz von Steiner ausgerechnet werden.
eines Körpers um eine bestimmte, durch den Schwerpunkt
gehende Drehachse bekannt ist, wenn aber der Körper um eine zu dieser Drehachse parallele Achse
rotiert, kann das neue Trägheitsmoment mit dem Satz von Steiner ausgerechnet werden.
| (4.269) |
wenn ![]() der Abstand der beiden Drehachsen ist.
der Abstand der beiden Drehachsen ist.
Beweis mit der kinetischen Energie.
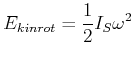 |
(4.270) |
Wir verschieben die Drehachse um ![]() , dann ist die Geschwindigkeit des Massenmittelpunktes bezüglich der
Drehachse
, dann ist die Geschwindigkeit des Massenmittelpunktes bezüglich der
Drehachse
![]() . Die kinetische Energie des
Massenmittelpunktes ist
. Die kinetische Energie des
Massenmittelpunktes ist
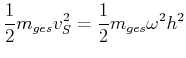 |
(4.271) |
Die gesamte kinetische Energie ist
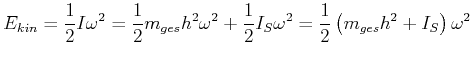 |
(4.272) |
Ein Vergleich der Klammer mit ![]() liefert das gewünschte Ergebnis.
liefert das gewünschte Ergebnis.
Bei flachen Körpern, das heisst bei Körpern, bei denen die Dicke oder die z-Ausdehnung verschwindend gegen die Ausdehnung in die x- und die y-Richtung ist, gilt
| (4.273) |
Da der Körper flach ist, ist sein Trägheitsmoment für Drehungen um die x-Achse oder um die y-Achse
nur von den Masseelementen und den Abständen in die y- oder die x-Richtung abhängig. Der Term ![]() wird also zu
wird also zu ![]() oder zu
oder zu ![]() . Damit ist
. Damit ist
![]() und
und
![]() . Bezüglich
der z-Achse müssen wir den Abstand quadrieren, um das Trägheitsmoment zu berechnen. Der Abstand
hängt von x und y, aber nicht von z ab.
. Bezüglich
der z-Achse müssen wir den Abstand quadrieren, um das Trägheitsmoment zu berechnen. Der Abstand
hängt von x und y, aber nicht von z ab.
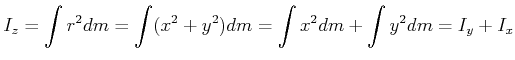 |
(4.274) |
| Dieser Stoff wurde am 20.11.2001 behandelt |
Analog zum linearen Impuls, der durch
![]() gegeben ist, hat ein Teilchen, das sich auf
einer Kreisbahn mit dem Radius r bewegt einen Drehimpuls, der mit seinem lineare Impuls
gegeben ist, hat ein Teilchen, das sich auf
einer Kreisbahn mit dem Radius r bewegt einen Drehimpuls, der mit seinem lineare Impuls ![]() wie folgt
zusammenhängt:
wie folgt
zusammenhängt:
| (4.275) |
Für allgemeine Bewegungen ist
wobei ![]() der senkrechte Abstand zur Drehachse ist. Wenn ein Teilchen parallel zur x-Achse in
der xy-Ebene am Nullpunkt entlang fliegt, dann kann man die z-Achse als Drehachse betrachten und
das Teilchen hat einen konstanten Drehimpuls!
der senkrechte Abstand zur Drehachse ist. Wenn ein Teilchen parallel zur x-Achse in
der xy-Ebene am Nullpunkt entlang fliegt, dann kann man die z-Achse als Drehachse betrachten und
das Teilchen hat einen konstanten Drehimpuls!
Sind mehrere Teilchen ![]() mit dem jeweiligen Drehimpuls
mit dem jeweiligen Drehimpuls
![]() , dann ist der
gesamte Drehimpuls
, dann ist der
gesamte Drehimpuls
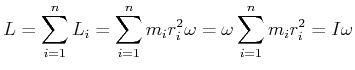 |
(4.277) |
Der Drehimpuls eines rotierenden Körpers ist
|
| Dieser Stoff wurde am 21.11.2001 behandelt |
Materialien
Folien zur Vorlesung am 21. 11. 2001 PDF
Analog zum zweiten Newtonschen Axiom kann für die Beziehung zwischen dem Drehimpuls und dem Drehmoment geschrieben werden
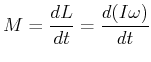 |
(4.279) |
Bei einem starren Körper (und nur da) ist ![]() und wir können schreiben
und wir können schreiben
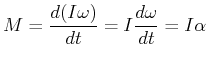 |
(4.280) |
Wenn kein äusseres Drehmoment auf einen Körper wirkt, ist
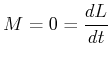 |
(4.281) |
also der Drehimpuls konstant.
|
Drehimpulserhaltung
Wenn das resultierende äussere
Drehmoment null ist, dann bleibt der Gesamtdrehimpuls eines Systems konstant. |
Weiter gilt
Das Drehmoment bezüglich des Schwerpunktes und die Änderung des Drehimpulses sind über
miteinander verknüpft. |
Beispiel:
Bei Tänzern oder Eiskunstläuferinnen ist das Drehmoment durch die Füsse (Kufen) sehr gering.
Deshalb ist der Drehimpuls in guter Näherung erhalten. Wenn die Arme an den Körper gezogen werden,
verringert sich ![]() , die Winkelgeschwindigkeit muss entsprechend zunehmen. In diesem Falle gilt
übrigens
, die Winkelgeschwindigkeit muss entsprechend zunehmen. In diesem Falle gilt
übrigens
![]() nicht; vielmehr ist
nicht; vielmehr ist
![]() .
.
Die kinetische Energie der Rotation wurde als
![]() geschrieben. Diese Gleichung kann umgeformt werden, so dass die
kinetische Energie als Funktion des Drehimpulses
gegeben ist.
geschrieben. Diese Gleichung kann umgeformt werden, so dass die
kinetische Energie als Funktion des Drehimpulses
gegeben ist.
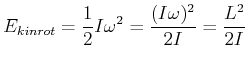 |
(4.283) |
| Dieser Stoff wurde am 21.11.2001 behandelt |
![\includegraphics[width=0.6\textwidth]{drehung-rad.eps}](img828.gif)
Rollen eines Rades ohne zu gleiten
|
Wenn ein Rad um den Winkel ![]() abrollt, legt die Drehachse (der Schwerpunkt) den Weg
abrollt, legt die Drehachse (der Schwerpunkt) den Weg
| (4.284) |
zurück. Der Schwerpunkt hat die Geschwindigkeit
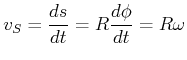 |
(4.285) |
Die Bedingung
![]() heisst Rollbedingung. Durch Ableiten dieser Gleichung erhält man
eine äquivalente Bedingung für die Beschleunigungen
heisst Rollbedingung. Durch Ableiten dieser Gleichung erhält man
eine äquivalente Bedingung für die Beschleunigungen
| (4.286) |
Beispiel:
Eine Kugel hat das Trägheitsmoment
![]() . Die kinetische
Energie der rollenden Kugel kann auf zwei Arten berechnet
werden:
. Die kinetische
Energie der rollenden Kugel kann auf zwei Arten berechnet
werden:
Beispiel:
Wie weit muss man in einem Billardspiel die Kugel oberhalb des Mittelpunktes treffen, damit sie
rollt. Die Distanzz oberhalb des Mittelpunktes sei x. Die Rollbedingung sagt:
![]() .
Die Drehmomentbedingung gibt
.
Die Drehmomentbedingung gibt
![]() . Teilt man die beiden Gleichungen durcheinander,
dann bekommt man
. Teilt man die beiden Gleichungen durcheinander,
dann bekommt man
![]() . Mit dem Trägheitsmoment einer Kugel
. Mit dem Trägheitsmoment einer Kugel
![]() bekommt man:
bekommt man:
![]() .
.
![\includegraphics[width=0.6\textwidth]{drehung-kugel-schief.eps}](img844.gif)
Kugel mit dem Radius R, die eine schiefe Ebene hinunterrollt.
|
Drehimpuls
| (4.287) |
Drehmoment hervorgerufen durch die Reibungskraft
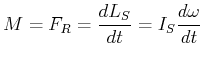 |
(4.288) |
![]() ist die Reibungskraft: wir brauchen Sie, um die Aufteilunfg in Drehmoment und lineare
Beschleunigung zu berechnen. Sie muss vorhanden sein, tritt aber im Schlussresultat nicht auf. Die
obige Gleichung kann auch als
ist die Reibungskraft: wir brauchen Sie, um die Aufteilunfg in Drehmoment und lineare
Beschleunigung zu berechnen. Sie muss vorhanden sein, tritt aber im Schlussresultat nicht auf. Die
obige Gleichung kann auch als
![]() geschrieben werden. Auf den Massenmittelpunkt
wirkt die Beschleunigungskraft
geschrieben werden. Auf den Massenmittelpunkt
wirkt die Beschleunigungskraft
![]() . Nun ist
. Nun ist
![]() . Wir erhalten
. Wir erhalten
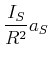 |
(4.289) |
Eingesetzt in die Beschleunigungsgleichung erhalten wir
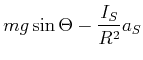 |
|||
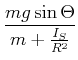 |
(4.290) |
Ohne Rotation wäre die Beschleunigung
![]() . Das Abrollen von einer Schiefen Ebene ist
langsamer als das abgleiten. Die Bedingung ist, dass
. Das Abrollen von einer Schiefen Ebene ist
langsamer als das abgleiten. Die Bedingung ist, dass
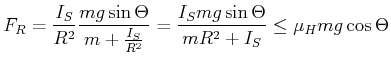 |
(4.291) |
ist6. Tabelle
gibt eine Übersicht über die Beschleunigungen verschiedener Körper. Man kann so zum
Beispiel herausfinden, ob ein Zylinder eine hohle Stahlröhre oder ein Aluminiumvollprofil
ist, wenn der Aussendurchmesser und das Gewicht gegeben sind. Weiter kann man mit dem
abrollen den Haftreibungskoeffizienten bestimmen. Man erhöht die Steigung so, dass der
Zylinder oder sonstige Körper ins gleiten kommt. Für einen Zylinder wird die Bedingung
![]() zu
zu
![]() oder
oder
| (4.292) |
Dieser Grenzwinkel heisst auch der Haftreibungswinkel. Er ist identisch mit dem Böschungswinkel bei Schüttgütern.
Energiebetrachtung für einen rollenden Zylinder:
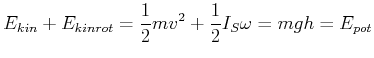 |
(4.293) |
Mit der Rollbedingung
Bei einem Zylinder
![]() ist das Resultat
ist das Resultat
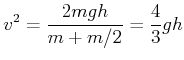 |
(4.295) |
| Dieser Stoff wurde am 21.11.2001 behandelt |
| Wenn man einen rotierenden Körper betrachtet, dann soll der Daumen der rechten Hand
parallel zur Drehachse sein. Die die Finger der rechten Hand zeigen in die Drehrichtung. Dann legt der Daumen die
Richtung des Vektors
|
Bei einer Schraube mit Rechtsgewinde zeigt der Daumen in die Vorschubrichtung.
Das Drehmoment hängt vom Winkel ![]() zwischen der Verbindungslinie
zwischen der Verbindungslinie ![]() zwischen der Drehachse und dem
Angriffspunkt der Kraft
zwischen der Drehachse und dem
Angriffspunkt der Kraft ![]() . Ist der Winkel
. Ist der Winkel ![]() , ist das Drehmoment maximal. Bei einem Winkel
0, wenn die Kraft und die Verbindungslinie parallel sind, ist das Drehmoment null. Die dazugehörige
Vektoroperation ist das Vektorprodukt
, ist das Drehmoment maximal. Bei einem Winkel
0, wenn die Kraft und die Verbindungslinie parallel sind, ist das Drehmoment null. Die dazugehörige
Vektoroperation ist das Vektorprodukt
| (4.296) |
Das Vektorprodukt oder das Kreuzprodukt ist durch
![]() gegeben, wobei
gegeben, wobei
![]() der Normalenvektor auf der von
der Normalenvektor auf der von ![]() und
und ![]() aufgespannten Ebene ist.
aufgespannten Ebene ist.
Einige Eigenschaften:
| (4.297) |
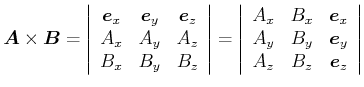 |
(4.298) |
Drehimpuls
| (4.299) |
Ausgeschrieben für den Fall dass ![]() und
und ![]() in der xy-Ebene liegen
in der xy-Ebene liegen
| (4.300) |
Der Drehimpuls liegt parallel zur Drehachse, so dass wir auch
| (4.301) |
haben.
Wenn ![]() die resultierende äussere Kraft ist, dann ist einerseits nach dem 2. Newtonschen Axiom
die resultierende äussere Kraft ist, dann ist einerseits nach dem 2. Newtonschen Axiom
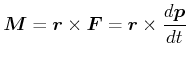 |
(4.302) |
und andererseits
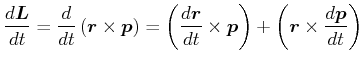 |
(4.303) |
Der erste Term ist null, da
![]() ist.
ist.
Also ist
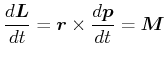 |
(4.304) |
|
|
| Dieser Stoff wurde am 21.11.2001 behandelt |
Es gibt zwei Arten, wie Reifen ausgewuchtet werden können:
Ein Rad kann dynamisch im Gleichgewicht sein und statisch nicht, oder umgekehrt.
| Dieser Stoff wurde am 21.11.2001 behandelt |
Wir haben bei der Gleichung (4.186) gesehen, dass
![]() ist. Wenn wir den Vektorcharakter der Drehungen
berücksichtigen, dann beobachtet man, dass
ist. Wenn wir den Vektorcharakter der Drehungen
berücksichtigen, dann beobachtet man, dass ![]() und
und
![]() nicht mehr parallel sind. In einem am
rotierenden Körper befestigten Koordinatensystem kann der Zusammenhang mit Hilfe des Trägheitstensors
geschrieben werden. Wir bemerken, dass
nicht mehr parallel sind. In einem am
rotierenden Körper befestigten Koordinatensystem kann der Zusammenhang mit Hilfe des Trägheitstensors
geschrieben werden. Wir bemerken, dass
| (4.305) |
Für jedes Volumenelement ![]() gilt
gilt
![]() . Also ist auch7
. Also ist auch7
So gilt für die ![]() -Komponente
-Komponente
und zyklisch permutiert für die anderen Koordinaten
![]() .
.
Die Gleichung (4.217) kann wie folgt interpretiert werden:
Würde
![]() entlang der x-Achse liegen, also nur die x-Komponente von null verschieden sein, dann ist das
erste Integral die schon bekannte Definition des Trägheitsmomentes. Die beiden anderen Momente, auch
Deviationsmomente genannt, sind nur dann von Null verschieden, wenn
entlang der x-Achse liegen, also nur die x-Komponente von null verschieden sein, dann ist das
erste Integral die schon bekannte Definition des Trägheitsmomentes. Die beiden anderen Momente, auch
Deviationsmomente genannt, sind nur dann von Null verschieden, wenn
![]() nicht parallel zur x-Achse
liegt. Analoges gilt auch für die y- und die z-Achse.
nicht parallel zur x-Achse
liegt. Analoges gilt auch für die y- und die z-Achse.
Gleichung (4.216) kann in Matrixschreibweise als
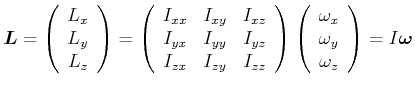 |
(4.308) |
wobei
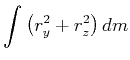 |
|||
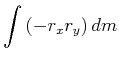 |
(4.309) |
ist. Jeder Tensor, also auch ![]() , kann durch die Rotation des Koordinatensystems so transformiert
werden, dass nur die Komponenten auf der Hauptdiagonalen von null verschieden sind. Wenn wir die
drei Komponenten als
, kann durch die Rotation des Koordinatensystems so transformiert
werden, dass nur die Komponenten auf der Hauptdiagonalen von null verschieden sind. Wenn wir die
drei Komponenten als
![]() (Hauptachsen) schreiben, kann die Stabilität von
Drehungen betrachtet werden. Wir nehmen an, dass eine Drehachse sich in der Nähe einer der
Hauptachsen befinde. Dann sind Drehungen um die
(Hauptachsen) schreiben, kann die Stabilität von
Drehungen betrachtet werden. Wir nehmen an, dass eine Drehachse sich in der Nähe einer der
Hauptachsen befinde. Dann sind Drehungen um die ![]() -Achse und um die
-Achse und um die ![]() -Achse stabil und um die
-Achse stabil und um die
![]() -Achse labil.
-Achse labil.
Wir definieren ein Trägheitsellipsoid, ein Ersatzkörper, der sich bezüglich Rotationen gleich wie der entsprechede allgemein geformte Ursprungskörper verhält.
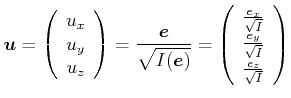 |
(4.310) |
Die Länge der einzelnen Halbachsen ist
![]() .
.
| Kreisel | Hauptträgheitsmomente | Trägheitsellipsoid |
|---|---|---|
| Kugel, Würfel, Tetraeder |
|
Kugel |
| axialsymmetrisch, tellerförmig |
|
Rotationsellipsoid, tellerförmig |
| axialsymmetrisch, spindelförmig |
|
Rotationsellipsoid, spindelförmig |
| niedrigsymmetrisch |
|
allgemeines Ellipsoid |
| Dieser Stoff wurde am 27.11.2001 behandelt |
Materialien
Ü&omega#omega;
wobei
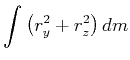 |
|||
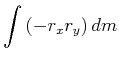 |
(4.311) |
ist. Jeder Tensor, also auch ![]() , kann durch die Rotation des Koordinatensystems so transformiert
werden, dass nur die Komponenten auf der Hauptdiagonalen von null verschieden sind. Wenn wir die
drei Komponenten als
, kann durch die Rotation des Koordinatensystems so transformiert
werden, dass nur die Komponenten auf der Hauptdiagonalen von null verschieden sind. Wenn wir die
drei Komponenten als
![]() (Hauptachsen) schreiben, kann die Stabilität von
Drehungen betrachtet werden. Wir nehmen an, dass eine Drehachse sich in der Nähe einer der
Hauptachsen befinde. Dann sind Drehungen um die
(Hauptachsen) schreiben, kann die Stabilität von
Drehungen betrachtet werden. Wir nehmen an, dass eine Drehachse sich in der Nähe einer der
Hauptachsen befinde. Dann sind Drehungen um die ![]() -Achse und um die
-Achse und um die ![]() -Achse stabil und um die
-Achse stabil und um die
![]() -Achse labil.
-Achse labil.
Wir definieren ein Trägheitsellipsoid, ein Ersatzkörper, der sich bezüglich Rotationen gleich wie der entsprechede allgemein geformte Ursprungskörper verhält.
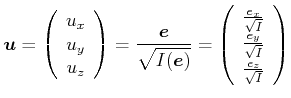 |
(4.312) |
Die Länge der einzelnen Halbachsen ist
![]() .
.
| Kreisel | Hauptträgheitsmomente | Trägheitsellipsoid |
|---|---|---|
| Kugel, Würfel, Tetraeder |
|
Kugel |
| axialsymmetrisch, tellerförmig |
|
Rotationsellipsoid, tellerförmig |
| axialsymmetrisch, spindelförmig |
|
Rotationsellipsoid, spindelförmig |
| niedrigsymmetrisch |
|
allgemeines Ellipsoid |
| Dieser Stoff wurde am 27.11.2001 behandelt |
Materialien
bungsblatt 7 vom 27. 11. 2001 (HTML oder PDF)
Folien zur Vorlesung am 27. 11. 2001 PDF
Ein Kreisel ist ein an einem Punkt auf der Drehachse unterstützer rotierender Körper. Dadurch, dass die Drehachse an einem Punkt fixiert ist, hat sie in zwei Richtungen, Azimut und Elevation, Bewegungsfreiheit. Die Bewegungen des Kreisels können in zwei Kategorien aufgeteilt werden, kräftefreie Bewegung (Nutation) und Bewegung unter äusseren Kräften (Präzession).
| Dieser Stoff wurde am 27.11.2001 behandelt |
![\includegraphics[width=0.6\textwidth]{kreisel1.eps}](img951.gif)
Kreisel mit Präzession
|
Auf diesen Kreisel wirkt die Gravitation an der Stelle des Rades. Die Kraft ![]() , die im Abstand
, die im Abstand ![]() vom Drehpunkt wirkt, bewirkt ein Drehmoment
vom Drehpunkt wirkt, bewirkt ein Drehmoment ![]() , das nach hinten gerichtet ist. Nun ist
, das nach hinten gerichtet ist. Nun ist ![]() ,
also muss
,
also muss ![]() parallel zu
parallel zu ![]() liegen. Dies ist nur möglich, wenn der Drehimpuls des Rades
liegen. Dies ist nur möglich, wenn der Drehimpuls des Rades
![]() ,
der in der horizontalen liegt, sich nach hinten dreht. Der Drehimpuls kann auch differenziell geschrieben
werden, indem man die Geometrie in der obigen Zeichnung verwendet:
,
der in der horizontalen liegt, sich nach hinten dreht. Der Drehimpuls kann auch differenziell geschrieben
werden, indem man die Geometrie in der obigen Zeichnung verwendet:
![]()
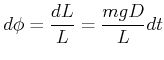 |
(4.313) |
Der Winkel ![]() beschreibt die Winkelpräzession.
beschreibt die Winkelpräzession.
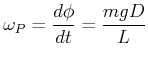 |
(4.314) |
| Dieser Stoff wurde am 27.11.2001 behandelt |
Wenn bei einem momentenfreien Kreisel die momentane Drehachse und die Hauptträgheitsachsen nicht parallel sind, rotiert die Drehachse um die Hauptträgheitsachse. Diese Bewegung sieht bei einem einseitig unterstützen momentenfreien Kreisel wie ein Nicken (Nutation) aus.
| Dieser Stoff wurde am 27.11.2001 behandelt |