Weiter: Erzwungene (gedämpfte) Schwingung und Oben: Schwingungen Zurück: Harmonische Schwingungen  Skript:  PDF-Datei Übungen:  Blätter

Unterabschnitte

• Güte des schwingungsfähigen Systems

Gedämpfte Schwingung

Dieser Stoff wurde am 15.1.2002 behandelt

(Siehe Tipler, Physik[Tip94, 401]) (Siehe Gerthsen, Physik[GV95, 150])

Eine genaue Beobachtung zeigt, dass die Amplitude jeder freie Schwingung sich nach einer gewissen, charakteristischen Zeit um einen bestimmten Betrag erniedrigt. Die Dämpfung ist in vielen Fällen proportional zur Geschwindigkeit

$$\vec{F}_D = - b\vec{v}$$ (8.472)

Das Kräftegleichgewicht ergibt

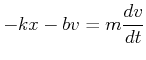$$-kx -b v = m\frac{dv}{dt}$$ (8.473)

Für kleine Dämpfungen ist die neue Resonanzfrequenz $\omega'$ in der Nähe von $\omega_0$. Mit jeder Schwingung nimmt die Energie $E_{tot} = E_{pot}(x_{max})= E_{kin}(v_{max}) = 2\left< E_{kin}\right> = \left<mv^2\right> = m\left<v^2\right>$ in einer definierten Zeiteinheit um einen bestimmten Betrag ab. Diese Leistung ist

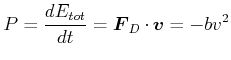$$P = \frac{dE_{tot}}{dt} = \vec{F}_D \cdot \vec{v}= -bv^2$$ (8.474)

Wenn wir $v^2$ durch $\left<v^2\right> = \frac{E_{tot}}{m}$ ersetzt, bekommt man

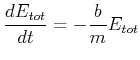$$\frac{dE_{tot}}{dt} = - \frac{b}{m}E_{tot}$$ (8.475)

Der Energiegehalt eines gedämpften Oszillators nimmt also exponentiell ab. Die relative Energieabnahme ist für alle Zeiten gleich. Wir lösen die Gleichung durch

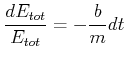$$\frac{dE_{tot}}{E_{tot}} = -\frac{b}{m}dt$$ (8.476)

und erhalten nach der Integration

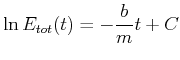$$\ln E_{tot}(t) = -\frac{b}{m} t + C$$ (8.477)

oder, nach einer Exponentiation

$$E_{tot}(t) = e^{-(b/m)t+C} = e^C\cdot e^{-(b/m) t} = E_0 e^{-(b/m)t}$$ (8.478)

Dieser Stoff wurde am 16.1.2002 behandelt

Materialien

Folien zur Vorlesung am 16. 01. 2002 PDF

Wir haben $E_0 = e^C$ gesetzt. Mit der Zeitkonstante $\tau = m/b$ bekommen wir

$$E = E_0 e^{-(b/m)t} = E_0 e^{-t/\tau}$$ (8.479)

Güte des schwingungsfähigen Systems

Dieser Stoff wurde am 16.1.2002 behandelt

Der Energieverlust pro Periode $T$ ist

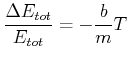$$\frac{\Delta E_{tot}}{E_{tot}} = -\frac{b}{m} T$$ (8.480)

Man charakterisiert die Dämpfung eines schwingungsfähigen Systems oft durch die Güte $Q$. Wenn der Energieverlust pro Periode $\Delta E_{tot}$ ist, gilt

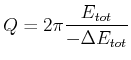$$Q = 2\pi \frac{E_{tot}}{-\Delta E_{tot}}$$ (8.481)

Der Q-Faktor ist umgekehrt zum relativen Energieverlust pro Periode

$$\frac{-\Delta E_{tot}}{E_{tot}} = \frac{2\pi}{Q}$$

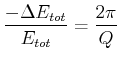
Es gilt auch

$$Q = 2\pi \frac{E_{tot}}{-\Delta E_{tot}} = 2\pi \frac{m}{bT} = 2\pi\frac{\tau}{T}$$ (8.482)

Da die Energie des Oszillators proportional zum Amplitudenquadrat ist ( $E_{tot} = \frac{1}{2} kx_{max}^2 = \frac{1}{2}kA^2$ gilt für die Amplitudenabnahme

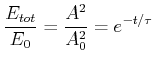$$\frac{E_{tot}}{E_0} = \frac{A^2}{A_0^2}=e^{-t/\tau}$$ (8.483)

Also ist

$$A = A_0 e^{-t/(2\tau)}$$ (8.484)

Die Lösung der Schwingungsgleichung für den gedämpften Oszillator ist

$$x(t) = A_0 e^{-(b/m)t}\cos(\omega' t + \delta)$$

$$\omega' = \omega_0\sqrt{1-\left(\frac{b}{2 m \omega_0}\right)^2} = \omega_0\sqrt{1-\frac{1}{4Q^2}}$$ (8.485)

Wenn die Dämpfung den kritischen Wert $b_k = 2 m\omega_0$ übertrifft, schwingt das System nicht mehr. Für $b=b_k$ nennt man das System kritisch gedämpft. Für $b>b_k$ ist es überkritisch gedämpft und für $b<b_k$ unterkristisch gedämpft.

Zum Beispiel verwendet man in Autos geschwindigkeitsproportionale Stossdämpfer um eine kritische Dämpfung zu erreichen. Sind die Stossdämpfer alt, wird die Dämpfung der Fahrzeugschwingungen, z.B. durch Bodenwellen angeregt, unterkritisch und man fliegt von der Strasse.

 Skript:  PDF-Datei Übungen:  Blätter