![\includegraphics[width=0.1\textwidth]{schwingung-getriebenes-pendel.eps}](img1518.gif)
Mit einem Exzenter angetriebenes Pendel
| Dieser Stoff wurde am 16.1.2002 behandelt |
![\includegraphics[width=0.1\textwidth]{schwingung-getriebenes-pendel.eps}](img1518.gif)
Mit einem Exzenter angetriebenes Pendel
|
Das vorliegende System wird durch zwei Grössen charakterisiert: die Anregungsschwingung
![]() sowie durch das Federpendel mit der Masse
sowie durch das Federpendel mit der Masse ![]() , der Dämpfung
, der Dämpfung ![]() und die Federkonstante
und die Federkonstante ![]() . Die
rücktreibende Kraft an der Feder ist
. Die
rücktreibende Kraft an der Feder ist
| (8.486) |
Die Beschleunigung ist wieder durch
![]() gegeben; die
geschwindigkeitsproportionale Dämpfung durch
gegeben; die
geschwindigkeitsproportionale Dämpfung durch
![]()
Die Bewegungsgleichung ist also
| (8.487) |
Wenn wir ![]() einsetzten und umstellen, erhalten wir
einsetzten und umstellen, erhalten wir
| (8.488) |
Wir teilen durch ![]() und kürzen
und kürzen
![]() ab und erhalten
ab und erhalten
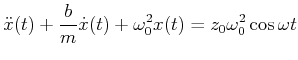 |
(8.489) |
Die Lösung (Simulation) dieser Gleichung besteht aus zwei Teilen: dem Einschwingvorgang als Lösung der Gleichung
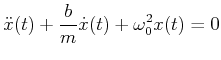
(analog zur freien gedämpften Schwingung, dieser Teil klingt ab gegen 0) sowie der stationären Lösung. Dieser Lösungsteil hat die Form
| (8.490) |
wobei wir hier ein Minuszeichen vor der Phase setzen, damit diese die Phasendifferenz zur Anregung darstellt. Eingesetzt in die Bewegungsgleichung erhalten wir
![$\displaystyle A(\omega)\left[-\omega^2 \cos(\omega t -\delta(\omega)) -\frac{b}...
...in(\omega t
-\delta(\omega)) + \omega_0^2\cos(\omega t - \delta(\omega))\right]$](img1530.gif) |
|||
| (8.491) |
Um die Gleichung zu lösen müssen wir die Winkelfunktionen ![]() und
und ![]() mit Phasen in
reine Winkelfunktionen auflösen. Also setzen wie
mit Phasen in
reine Winkelfunktionen auflösen. Also setzen wie
![]() und
und
![]() . Wir bekommen dann
. Wir bekommen dann
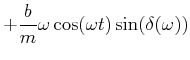 |
|||
| 0 | |||
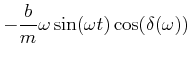 |
|||
| (8.492) |
Diese Gleichungen können vereinfacht werden
![$\displaystyle A(\omega)\left[-\omega^2 \cos(\delta(\omega))
+\frac{b}{m}\omega\sin(\delta(\omega))
+ \omega_0^2\cos(\delta(\omega))\right]$](img1543.gif) |
|||
| 0 | 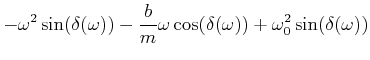 |
(8.493) |
Aus der zweiten Gleichung folgt
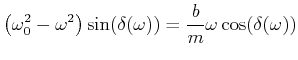 |
(8.494) |
und daraus
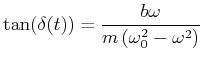 |
(8.495) |
Wir verwenden
![]() und
und
![]() und bekommen aus der ersten Gleichung
und bekommen aus der ersten Gleichung
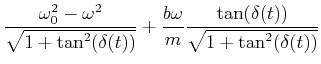 |
|||
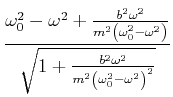 |
|||
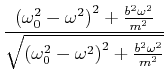 |
|||
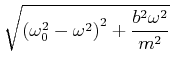 |
(8.496) |
Zusammengefasst ist die stationäre Lösung durch die Amplitude und Phase
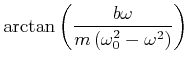 |
(8.497) | ||
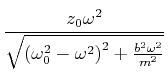 |
(8.498) |
Mit der Definition der Güte aus Gleichung (8.52) sowie mit
![]() schreiben wir zuerst
schreiben wir zuerst
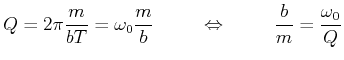 |
(8.499) |
und erhalten
|
Noch kompakter ist die folgende Schreibweise für die Amplitude
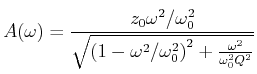 |
(8.502) |
Die Frequenz, bei der die Amplitude maximal wird, also die Resonanzfrequenz, ist
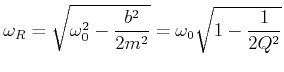 |
(8.503) |
Diese Frequenz, die durch die Gleichung
![]() definiert ist, ist
kleiner als die Eigenfrequenz eines gedämpften Systems (Siehe Gleichung (8.55) ).
definiert ist, ist
kleiner als die Eigenfrequenz eines gedämpften Systems (Siehe Gleichung (8.55) ).
Bei der Resonanzfrequenz des ungedämpften Systems gegeben durch
Die Steigung der Phase
Es ist sehr viel einfacher, |