![\includegraphics[width=0.8\textwidth]{schwingung-masse-feder.eps}](img1391.gif)
Masse-Feder-System als Modell eines schwingungsfähigen Systems
| Dieser Stoff wurde am 9. 1. 2002 behandelt |
![\includegraphics[width=0.8\textwidth]{schwingung-masse-feder.eps}](img1391.gif)
Masse-Feder-System als Modell eines schwingungsfähigen Systems
|
Die Kraft auf die Masse ist durch
| (8.431) |
gegeben, wobei ![]() die Federkonstante ist. Durch diese Kraft wird die Masse beschleunigt, so dass
die Federkonstante ist. Durch diese Kraft wird die Masse beschleunigt, so dass
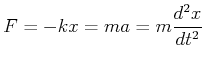
Umgeschrieben erhalten wir die Bewegungsgleichung
Die Beschleunigung ist also proportional zur Auslenkung. Traditionellerweise wird die obige Gleichung auch als
| Frequenzen werden in Hertz |
Die Lösung der Gleichung (8.3) ist
| (8.434) |
Diese Lösung wird durch die
Simulation
illustriert. Die Phase ist nur bis auf ein ganzzahliges Vielfaches von ![]() bestimmt
(Eigenschaft der Winkelfunktionen). Die Position beim Nulldurchgang ist
bestimmt
(Eigenschaft der Winkelfunktionen). Die Position beim Nulldurchgang ist
![]() .
.
| Ist die Beschleunigung eines Gegenstandes proportional zu seiner Auslenkung und dieser entgegengesetzt, so führt der Gegenstand eine einfache harmonische Schwingung durch. |
Die Geschwindigkeit der Masse ist
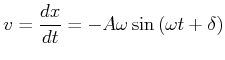 |
(8.435) |
Die Geschwindigkeit bei ![]() ist
ist
![]() . Da von den drei die
Schwingung bestimmenden Grössen zwei,
. Da von den drei die
Schwingung bestimmenden Grössen zwei, ![]() und
und ![]() unbekannt sind, reicht die
Kenntnis der Position zur Zeit
unbekannt sind, reicht die
Kenntnis der Position zur Zeit ![]() und der Geschwindigkeit zu dieser gleichen Zeit aus,
um die Schwingungsform zu bestimmen.
und der Geschwindigkeit zu dieser gleichen Zeit aus,
um die Schwingungsform zu bestimmen.
Die Beschleunigung ist
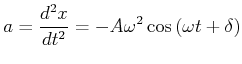 |
(8.436) |
Mit Gleichung (8.2) kann man schreiben
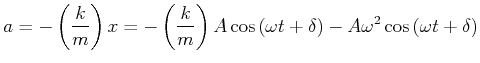 |
(8.437) |
und damit
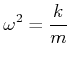 |
(8.438) |
Damit sind die Frequenz und die Schwingungsdauer
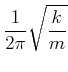 |
|||
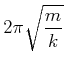 |
(8.439) |
| Die Schwingungsdauer hängt nicht von der Amplitude ab (lineares System). |
| Dieser Stoff wurde am 9. 1. 2001 behandelt |
![\includegraphics[width=0.5\textwidth]{schwingungen-kreisbewegung.eps}](img1412.gif)
Zusammenhang zwischen der Kreisbewegung und einer Schwingung
|
Da die Funktionen
![]() und
und
![]() beide die
Schwingungsgleichung erfüllen, kann geschlossen werden, dass eine
harmonische Schwingung die Projektion einer Kreisbewegung ist (siehe auch die
Simulation).
Nach der Definition des Cosinus ist die Projektion des umlaufenden Radius
beide die
Schwingungsgleichung erfüllen, kann geschlossen werden, dass eine
harmonische Schwingung die Projektion einer Kreisbewegung ist (siehe auch die
Simulation).
Nach der Definition des Cosinus ist die Projektion des umlaufenden Radius ![]() auf die
auf die
![]() -Achse gerade der Cosinus.
-Achse gerade der Cosinus.
| Dieser Stoff wurde am 9. 1. 2001 behandelt |
Die potentielle Energie einer um die Länge ![]() ausgelenkten Feder ist
ausgelenkten Feder ist
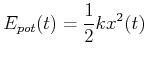 |
(8.440) |
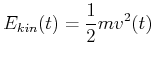 |
(8.441) |
Beide Energien hängen von der Zeit ab. Die Erhaltung der mechanischen Energie fordert
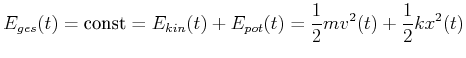 |
(8.442) |
Am Umkehrpunkt, bei der maximalen Auslenkung
![]() ist die Geschwindigkeit
ist die Geschwindigkeit
![]() . Also ist bei einem harmonischen Oszillator
. Also ist bei einem harmonischen Oszillator
die Gesamtenergie. |
Setzen wir die Lösung
![]() und damit auch
und damit auch
![]() jeweils ein, erhalten
wir
jeweils ein, erhalten
wir
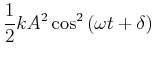 |
|||
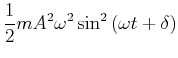 |
|||
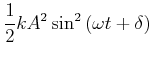 |
(8.444) |
wobei wir
![]() verwendet haben. Die Gesamtenergie ist
verwendet haben. Die Gesamtenergie ist
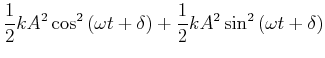 |
|||
![$\displaystyle \frac{1}{2} k A^2 \left[\sin^2\left( \omega t +
\delta\right)+\cos^2 \left(\omega t + \delta\right)\right]$](img1431.gif) |
|||
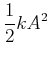 |
(8.445) |
unabhängig von ![]() . Der Energiegehalt eines harmonischen Oszillators pendelt zwischen
zwei Energiereservoirs, hier der kinetischen und der potentiellen Energie, hin
und her.
. Der Energiegehalt eines harmonischen Oszillators pendelt zwischen
zwei Energiereservoirs, hier der kinetischen und der potentiellen Energie, hin
und her.
| Immer dann, wenn in einem System zwei Energiereservoirs gekoppelt sind und Energie zwischen ihnen ausgetauscht wird, ist das System ein Oszillator. |
Beispiele:
Die kinetische und die potentielle
Energie können mit dem Winkel der momentanen Phase
![]() wie folgt geschrieben werden:
wie folgt geschrieben werden:
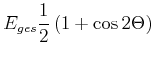 |
|||
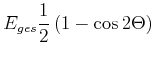 |
(8.446) |
Damit ist auch sofort klar, dass die Mittelwerte
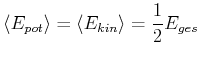 |
(8.447) |
sind.
| Dieser Stoff wurde am 9.1.2002 behandelt |
![\includegraphics[width=0.6\textwidth]{schwingungen-schwerefeld.eps}](img1439.gif)
Schwingendes System im Schwerefeld
|
Eine Feder im Schwerefeld mit Masse wird durch die Bewegungsgleichung
beschrieben (1.
Simulation
und
2.
Simulation). Die Ruhelage ist
durch
![]() gegeben. Also ist
gegeben. Also ist
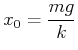 |
(8.449) |
Wir wissen, wie wir ein Feder-Masse-System berechnen müssen, wenn wir die Koordinate
![]() verwenden. Da die beiden Koordinatensysteme
verwenden. Da die beiden Koordinatensysteme ![]() und
und ![]() sich nur um eine
Konstante unterscheiden, sind die ersten Ableitungen
sich nur um eine
Konstante unterscheiden, sind die ersten Ableitungen
![]() und
die zweiten Ableitungen
und
die zweiten Ableitungen
![]() gleich. Deshalb wird
Gleichung (8.18)
gleich. Deshalb wird
Gleichung (8.18)
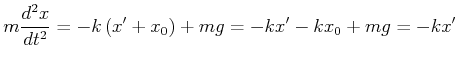 |
(8.450) |
da ![]() ist. Damit erhalten wir die bekannte Lösung
ist. Damit erhalten wir die bekannte Lösung
| (8.451) |
Die potentielle Energie bezogen auf die neue
Gleichgewichtslage ![]() ist
ist
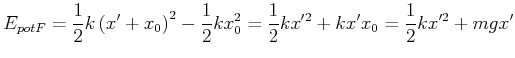 |
(8.452) |
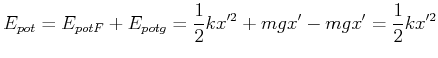 |
(8.453) |
| Dieser Stoff wurde am 15.1.2002 behandelt |
Materialien
Übungsblatt 12 vom 15. 1. 2002 (HTML oder PDF)
Folien zur Vorlesung am 15. 01. 2002 PDF
![\includegraphics[width=0.6\textwidth]{schwingung-pendel.eps}](img1453.gif)
Mathematisches Pendel im Schwerefeld
|
Ein mathematisches Pendel ist eine Punktmasse ![]() aufgehängt an einem masselosen Faden
der Länge
aufgehängt an einem masselosen Faden
der Länge ![]() .
.
Der vom Pendel zurückgelegte Weg ist die Bogenlänge
| (8.454) |
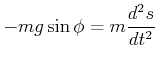 |
(8.455) |
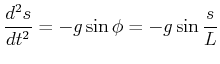 |
(8.456) |
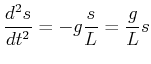 |
(8.457) |
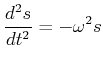 |
(8.458) |
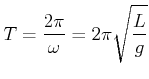 |
(8.459) |
Für grosse Amplituden ist die Schwingungsdauer durch die Reihenentwicklung
![$\displaystyle T = 2\pi\sqrt{\frac{L}{g}}\left[1+\frac{1}{2^2}\sin^2\left(\frac{...
...t(\frac{3}{4}\right)^2\sin^4\left(\frac{1}{2}\frac{s_0}{L}\right)+\ldots\right]$](img1465.gif) |
(8.460) |
![\includegraphics[width=0.4\textwidth]{schwingung-phys-pendel.eps}](img1466.gif)
Physikalisches Pendel.
|
Wir müssen nun mit dem Trägheitsmoment des Pendels
bezüglich des Drehpunktes ![]() rechnen. Das Drehmoment ist
rechnen. Das Drehmoment ist
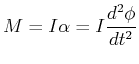 |
(8.461) |
Die Bewegungsgleichung ist also
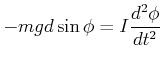 |
(8.462) |
In der traditionellen Schreibweise lautet die Bewegungsgleichung
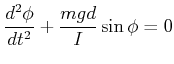 |
(8.463) |
Mit
![]() und unter der Annahme einer kleinen Amplitude ist das
physikalische Pendel ein harmonischer Oszillator mit der Bewegungsgleichung
und unter der Annahme einer kleinen Amplitude ist das
physikalische Pendel ein harmonischer Oszillator mit der Bewegungsgleichung
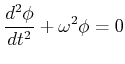 |
(8.464) |
Die Schwingungsdauer ist
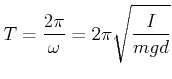 |
(8.465) |
Eine Anwendungsmöglichkeit dieser Gleichung ist die Bestimmung des Trägheitsmomentes eines Körpers
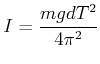 |
(8.466) |
Zum Beispiel ist für einen einseitig eingespannten Stab das Trägheitsmoment nach
Gleichung (4.176)
![]() . Der Schwerpunkt liegt in der Mitte,
also
. Der Schwerpunkt liegt in der Mitte,
also
![]() . Damit wird die Schwingungsdauer
. Damit wird die Schwingungsdauer
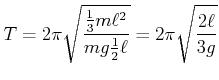
Vergleiche dies mit dem Resultat für ein mathematisches Pendel
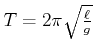 .
.
![\includegraphics[width=0.5\textwidth]{schwingung-torsions-pendel.eps}](img1478.gif)
Torsionspendel (analog zur Gravitationswage)
|
Das rückstellende Moment ist proportional zum Verdrillungswinkel und dient zur
Winkelbeschleunigung des Drehkörpers mit dem Trägheitsmoment ![]()
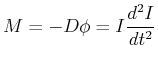 |
(8.467) |
Wieder setzen wir
![]() . Die Periodendauer ist
. Die Periodendauer ist
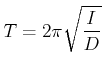 |
(8.468) |
| Dieser Stoff wurde am 15.1.2002 behandelt |
Wir nehmen eine allgemeine Potentialfunktion
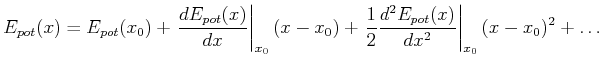 |
(8.469) |
an und entwickeln sie in eine Taylorreihe um den Punkt ![]() . Dieser Punkt soll ein
Gleichgewichtspunkt sein
. Dieser Punkt soll ein
Gleichgewichtspunkt sein
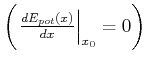 . Dann ist die
Kraft
. Dann ist die
Kraft
![]() als Funktion durch die erste Ableitung der potentiellen
Energie gegeben. Die Steigung der Kraft-Distanz-Kurve, die Federkonstante
als Funktion durch die erste Ableitung der potentiellen
Energie gegeben. Die Steigung der Kraft-Distanz-Kurve, die Federkonstante ![]() ist durch die zweite
Ableitung gegeben.
ist durch die zweite
Ableitung gegeben.
Also kann an jedem Gleichgewichtspunkt bei genügend kleinen Auslenkungen die Schwingungsgleichung
| 0 | 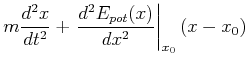 |
||
| 0 | 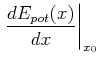 |
(8.470) |
geschrieben werden. Die Schwingungsdauer für kleine Bewegungen ist
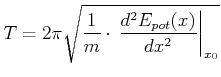 |
(8.471) |