| Dieser Stoff wurde am 16.1.2002 behandelt |
Wenn in der ![]() -Richtung eine Schwingung
-Richtung eine Schwingung
![]() und in der
und in der
![]() -Richtung eine Schwingung
-Richtung eine Schwingung
![]() überlagert werden,
entstehen Lissajous-Figuren. Solche Schwingungen können entstehen, wenn zum Beispiel eine
Kugel in einer elliptischen Potentialmulde hin- und herschwingt.
überlagert werden,
entstehen Lissajous-Figuren. Solche Schwingungen können entstehen, wenn zum Beispiel eine
Kugel in einer elliptischen Potentialmulde hin- und herschwingt.
![\includegraphics[width=0.7\textwidth]{schwingungen-ueberlagerung.eps}](img1571.gif)
Zeigerdiagramm. Links für zwei Zeiten, in der Mitte das Zeigerdiagramm für zwei Schwingungen (rot) und (blau) mit der Summe (grün) und rechts die Winkel.
|
Eine Schwingung
![]() kann durch einen Zeiger dargestellt
werden. Die Projektion dieses Zeigers auf die x-Achse ergibt das Schwingungsbild.
kann durch einen Zeiger dargestellt
werden. Die Projektion dieses Zeigers auf die x-Achse ergibt das Schwingungsbild.
Wenn zwei Schwingungen unterschiedlicher Amplitude und Phase, aber gleicher Frequenz addiert werden, kann man die trigonometrischen Sätze für schiefwinklige Dreiecke anwenden. So ist nach dem Cosinussatz
| (8.506) |
oder
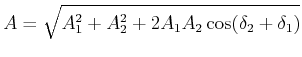 |
(8.507) |
Der Sinussatz liefert
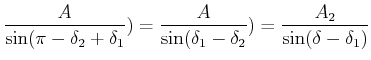 |
(8.508) |
Wenn wir die Zeit zur Berechnung so wählen, dass
![]() ist, so ergibt sich
ist, so ergibt sich
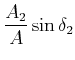 |
|||
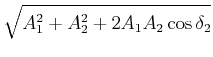 |
(8.509) |
| Dieser Stoff wurde am 22.1.2002 behandelt |
Materialien
Übungsblatt 13 vom 22. 1. 2002 (HTML oder PDF)
Folien zur Vorlesung am 22. 01. 2002 PDF
Die Frequenzen der beiden Schwingungen sollen um
![]() verschieden sein. Wir
setzen an
verschieden sein. Wir
setzen an
| (8.510) |
Die resultierende Schwingung ist
| (8.511) |
Wir rechnen nun wie folgt um
Dies entspricht einer Schwingung der Frequenz ![]() mit einer aufmodulierten Frequenz
mit einer aufmodulierten Frequenz
![]() . Wir nennen diese verhalten auch Schwebung. Transparenter wird die
Rechnung, wenn komplexe Zahlen verwendet werden. Anstelle von
. Wir nennen diese verhalten auch Schwebung. Transparenter wird die
Rechnung, wenn komplexe Zahlen verwendet werden. Anstelle von
![]() schreiben wir
schreiben wir
![]() , wobei wieder
, wobei wieder
![]() ist. Wir schreiben
ist. Wir schreiben
| (8.513) |
und weiter
| (8.514) |
| Dieser Stoff wurde am 22.1.2002 behandelt |
Die obige Schwingung ist nicht nur durch den zeitlichen Verlauf, sondern auch durch das
Frequenzspektrum sowie das Phasenspektrum charakterisiert. Grundlage für
diese Aussage ist der Mathematische Satz, dass sich jede periodische Funktion
![]() (Frequenz
(Frequenz
![]() als Fourierreihe
als Fourierreihe
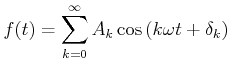 |
(8.515) |
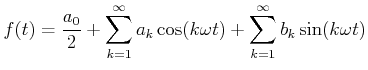 |
(8.516) |
Für gerade Funktionen
![]() sind alle
sind alle ![]() , für ungerade Funktionen sind alle
, für ungerade Funktionen sind alle
![]() .
.
![\includegraphics[width=0.8\textwidth]{schwingung_fourier_synth.eps}](img1606.gif)
Synthese einer Schwingung mit
|
![\includegraphics[width=0.8\textwidth]{schwingung_fourier_synth_1.eps}](img1608.gif)
Synthese einer Schwingung mit
|
![\includegraphics[width=0.8\textwidth]{schwingung_fourier_synth_2.eps}](img1610.gif)
Synthese einer Schwingung mit
|
![\includegraphics[width=0.8\textwidth]{schwingung_fourier_synth_3.eps}](img1612.gif)
Synthese einer Schwingung mit
|
![\includegraphics[width=0.8\textwidth]{schwingung_fourier_synth_4.eps}](img1614.gif)
Synthese einer Schwingung mit
|
![\includegraphics[width=0.8\textwidth]{schwingung_fourier_synth_5.eps}](img1616.gif)
Synthese einer Schwingung mit
|
Die folgenden Applets illustrieren die Fourieranalyse und -synthese