

Up: Physik 1 für Ingenieure
Übungsblatt 8
Physik für Ingenieure 1
Othmar Marti, (othmar.marti@physik.uni-ulm.de)
4. 12. 2001
Statische Gleichgewichte, Gravitation,
PDF-Datei
- Bei einem Kollergang wird ein Rad der Masse
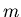 im Kreis um eine zentrale Befestigung geführt
und rollt in der Horizontalebene, wobei die Radachse (masselos) in 0 gelenkig und reibungsfrei
gelagert sei. Berechne den Normaldruck als Funktion der Winkelgeschwindigkeit
im Kreis um eine zentrale Befestigung geführt
und rollt in der Horizontalebene, wobei die Radachse (masselos) in 0 gelenkig und reibungsfrei
gelagert sei. Berechne den Normaldruck als Funktion der Winkelgeschwindigkeit 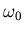 der
Radumdrehung. Was ist das Resultat für
der
Radumdrehung. Was ist das Resultat für 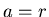 ?
?
- Ihnen steht eine Waage mit einer Auflagefläche von
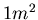 und einer Höhe von 10 cm sowie 7 Holzplatten
zur mit der Fläche
und einer Höhe von 10 cm sowie 7 Holzplatten
zur mit der Fläche 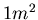 und einer Höhe von 10 cm
Verfügung. Sie sollen das Gesamtgewicht eines Lastzuges mit einer 2-achsigen Zugmaschine sowie
einem zweiachsigen Sattelauflieger nachmessen. Geht das? Was ist die Messvorschrift?
Diskutieren Sie das Problem unter dem Gesichtspunkt der Gleichgewichtsbedingungen.
und einer Höhe von 10 cm
Verfügung. Sie sollen das Gesamtgewicht eines Lastzuges mit einer 2-achsigen Zugmaschine sowie
einem zweiachsigen Sattelauflieger nachmessen. Geht das? Was ist die Messvorschrift?
Diskutieren Sie das Problem unter dem Gesichtspunkt der Gleichgewichtsbedingungen.
- Zwei Punktmassen der Grösse
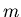 sind auf der y-Achse im Abstand
sind auf der y-Achse im Abstand 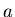 symmetrisch auf beiden Seiten des
Nullpunkts plaziert (Ihre Koordinaten sind
symmetrisch auf beiden Seiten des
Nullpunkts plaziert (Ihre Koordinaten sind 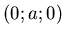 und
und 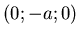 .
.
- Ein drittes Teilchen
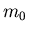 befinde sich im Abstand
befinde sich im Abstand 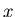 vom Ursprung auf der x-Achse. Zeigen
Sie, dass die Kraft, die von den beiden Punktmassen auf dieses Teilchen ausgeübt wird,
gegeben ist durch
vom Ursprung auf der x-Achse. Zeigen
Sie, dass die Kraft, die von den beiden Punktmassen auf dieses Teilchen ausgeübt wird,
gegeben ist durch
- Ermitteln Sie das durch die beiden Massen auf der y-Achse hervorgerufene
Gravitationsfeld
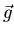 auf der x-Achse.
auf der x-Achse.
- Zeigen Sie, dass die von den beiden auf der y-Achse befindlichen Massen
hervorgerufene Gravitationsfeldstärke
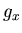 annähernd
annähernd 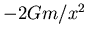 ist, wenn
ist, wenn 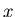 wesentlich
grösser als
wesentlich
grösser als 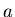 ist.
ist.
- Zeigen sie, dass
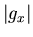 an den Punkten
an den Punkten
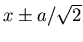 maximal ist.
maximal ist.
- Io, einer der Jupitermonde, hat einen mittleren Bahnradius von
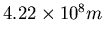 und eine
Umlaufdauer von
und eine
Umlaufdauer von
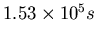 .
.
- Bestimmen Sie den mittleren Bahnradius von Callisto, einem anderen Jupitermond,
dessen Umlaufzeit
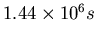 betrage.
betrage.
- Berechnen Sie mit dem bekannten Wert von G die Jupitermasse.
- Zwei Planeten gleicher Masse bewegen sich um einen Stern mit wesentlich grösserer Masse.
Planet 1 mit der Masse
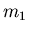 bewege sich auf einer Kreisbahn mit dem Radius
bewege sich auf einer Kreisbahn mit dem Radius
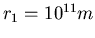 . Seine Umlaufdauer betrage 2 Jahre. Planet 2 mit der Masse
. Seine Umlaufdauer betrage 2 Jahre. Planet 2 mit der Masse 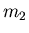 bewege sich
auf einer elliptischen Bahn, wobei der Kleinste Abstand zum Stern
bewege sich
auf einer elliptischen Bahn, wobei der Kleinste Abstand zum Stern 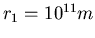 (Punkt P) und der grösste
Abstand
(Punkt P) und der grösste
Abstand
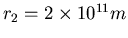 (Punkt A) betrage.
(Punkt A) betrage.
- Berechnen sie die Umlaufdauer von Planet 2. Berücksichtigen Sie dabei, dass der
mittlere Bahnradius einer elliptischen Bahn gleich der Länge der grossen Halbachse ist.
- Wie gross ist die Masse des Sternes?
- Welcher Planet hat die grössere Gesamtenergie?
- Welcher Planet hat am Punkt P die grössere Geschwindigkeit?
- Welche Geschwindigkeit besitzt Planet 2 im Punkt P im Vergleich zur Geschwindigkeit
im Punkt A?
-
- Das Rad legt den Weg
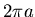 zurück und dreht sich dabei
zurück und dreht sich dabei
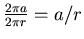 mal. Also ist
mal. Also ist
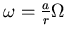 .
.
- Wenn
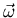 nach rechts zeigt, muss
nach rechts zeigt, muss 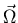 nach unten zeigen.
nach unten zeigen.
-
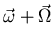 zeigt auf den Mittelpunkt der Auflagelinie.
zeigt auf den Mittelpunkt der Auflagelinie.
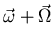 ist die momentane Drehachse.
ist die momentane Drehachse.
- Der Drehimpuls des Rades zeigt nach rechts.
-
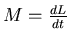
- Die Drehimpulsänderung durch
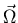 bewirkt ein Drehmoment. In der Zeit
bewirkt ein Drehmoment. In der Zeit 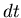 ändert sich
ändert sich
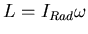 um
um
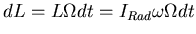
- also ist
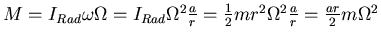 .
.
- Die resultierende Normalkraft minus die Gewichtskraft ist das Drehmoment und gleich
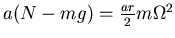 und damit
und damit
-
![$N = mg + \frac{r}{2} m \Omega^2 = m\left[g + \frac{r}{2} \Omega^2\right]$](img37.gif)
- Wenn man sich den Kollergang als Gewichtsbehafteten Kreisel vorstellt, wäre die Normalkraft genau
dann null, wenn sich der Kreisel mit
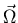 nach oben zeigend bewegen würde. Dann ist die
Gewichtskraft durch das Reaktionsdrehmoment des Kreisels kompensiert. Ist
nach oben zeigend bewegen würde. Dann ist die
Gewichtskraft durch das Reaktionsdrehmoment des Kreisels kompensiert. Ist
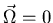 , ist die Normalkraft
, ist die Normalkraft 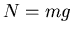 , da wir mit dieser Kraft unterstützen müssen. Dreht
der Kreisel wie in diesem Falle entgegengesetzt der Präzessionsrichtung, muss
, da wir mit dieser Kraft unterstützen müssen. Dreht
der Kreisel wie in diesem Falle entgegengesetzt der Präzessionsrichtung, muss 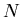 entsprechend grösser werden!
entsprechend grösser werden!
- Wir nummerieren die acht Räder mit
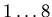 . Jeweils ein Rad, Rad Nummer
. Jeweils ein Rad, Rad Nummer 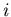 steht
auf der Waage, die anderen auf dem Holz. Da alle Untersätze die gleiche Höhe haben, ist die
Gewichtsverteilung wie vorher.
steht
auf der Waage, die anderen auf dem Holz. Da alle Untersätze die gleiche Höhe haben, ist die
Gewichtsverteilung wie vorher.
- Es gilt
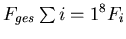 , wenn
, wenn 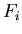 die Auflagekraft des Rades
die Auflagekraft des Rades 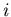 ist.
ist.
- Bemerkung Nach dieser Methode kann das zulässige Gesamtgewicht und die zulässige Achslast
mit mobilen Einrichtungen überprüft werden.
- Wenn Sie Gleichgewichte betrachten, dann muss die Summe aller Kräfte und die Summe
aller Drehmomente bezüglich des Schwerpunkts null sein. Mit der Momentengleichung können
Sie die Last auf jedem Rad berechnen.
- Zwei Punktmassen der Grösse
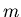 sind auf der y-Achse im Abstand
sind auf der y-Achse im Abstand 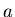 symmetrisch auf beiden Seiten des
Nullpunkts plaziert (Ihre Koordinaten sind
symmetrisch auf beiden Seiten des
Nullpunkts plaziert (Ihre Koordinaten sind 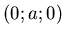 und
und 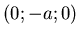 .
.
- Verbindungsvektor
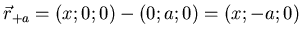 und
und
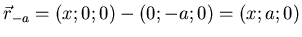
- Länge der Vektoren
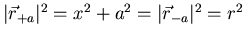
- Die y-Komponenten der Gravitationskräfte der einzelnen Massen sind vom Betrage
her gleich gross, haben aber verschiedenes Vorzeichen: also gibt es nur die
x-Komponente der Gravitation.
- Mit einem pythagoräischen Dreieck, bei dem die Hypotenuse 1 ist, errechnet man:
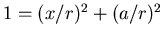 . Also ist
. Also ist
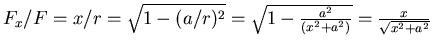
- Die Gravitationskraft ist also
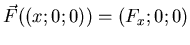 und
und
![$F_x = \left[-\frac{Gm
m_0}{r_{+a}^2}\right]\frac{x}{\sqrt{x^2+a^2}}+\left[-\frac{Gm
m_0}{r_{-a}^2}\right]\frac{x}{\sqrt{x^2+a^2}}$](img51.gif)
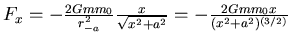 .
.
- Damit ist die Gleichung
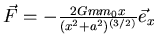 gezeigt.
gezeigt.
-
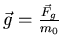 und damit
und damit
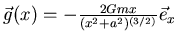
-
- Maximum oder Minimum: Ableitung = 0.
-
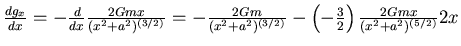
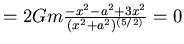
- Also
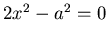 und
und 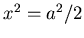
- Damit folgt die Behauptung.
- 3. Keplersches Gesetz:
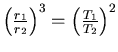 .
.
-
![$r_1 = \sqrt[3]{\left(\frac{T_1}{T_2}\right)^2}r_2 =
\sqrt[3]{\left(\frac{1.44\times 10^6 s}{1.53\times 10^5 s}\right)^2}4.22\times 10^8
m = 1.88\times 10^9 m$](img65.gif)
-
- Zwei Planeten gleicher Masse bewegen sich um einen Stern mit wesentlich grösserer Masse.
Planet 1 mit der Masse
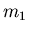 bewege sich auf einer Kreisbahn mit dem Radius
bewege sich auf einer Kreisbahn mit dem Radius
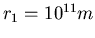 . Seine Umlaufdauer betrage 2 Jahre. Planet 2 mit der Masse
. Seine Umlaufdauer betrage 2 Jahre. Planet 2 mit der Masse 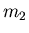 bewege sich
auf einer elliptischen Bahn, wobei der Kleinste Abstand zum Stern
bewege sich
auf einer elliptischen Bahn, wobei der Kleinste Abstand zum Stern 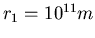 (Punkt P) und der grösste
Abstand
(Punkt P) und der grösste
Abstand
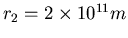 (Punkt A) betrage.
(Punkt A) betrage.
- Grosse Halbachse:
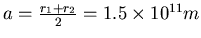
-
![$T_2 = \sqrt[2]{\left(\frac{a}{r_1}\right)^3}T_1 =
\sqrt[2]{\left(\frac{1.5 \times 10^{11} m}{1\times 10^{11} m}\right)^3} 2J
= 3,67 J$](img71.gif)
-
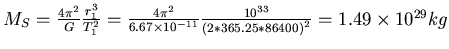
- Die Gesamtenergie eines Planeten ist
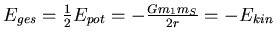
- Planet 2 hat also die grössere Gesamtenergie, da die grosse Halbachse seiner
Bahn grösser als Bei Plante 1 ist, die potentielle Energie also weniger negativ
ist.
Welcher Planet hat die grössere Gesamtenergie?
- Am Punkt P haben beide Planeten die gleiche potentielle Energie
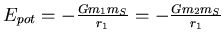 .
.
- Die kinetische Energie ist
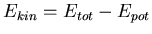
- Also ist
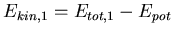 und
und
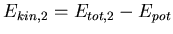
-
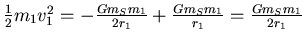
-
![$\frac{1}{2}m_2 v_2^2 = -\frac{G m_S m_2}{2 a}+\frac{G m_S m_1}{r_1} =
-\frac{G...
...}\left[1-\frac{r_1}{r_1+r_2}\right]
= \frac{G m_S m_1}{r_1}\frac{r_2}{r_1+r_2}$](img79.gif)
-
![$\left(\frac{v_1}{v_2}\right)^2 = \frac{r_1}{2 r_1
\left[1-\frac{r_1}{r_1+r_2}\right]} = \frac{r_1+r_2}{2 r_2} = \frac{1}{2}\left(1+\frac{r_1}{r_2}\right)$](img80.gif)
- Da
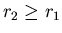 ist, ist
ist, ist
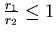 und also
und also 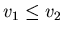
- Mit dem 2. Keplerschen Gesetz ist
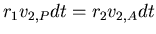
- Also
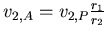
Übungsblatt 8
Physik für Ingenieure 1
This document was generated using the
LaTeX2HTML translator Version 99.2beta8 (1.46)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html uebungsblatt8
The translation was initiated by marti on 2002-09-12


Up: Physik 1 für Ingenieure
Othmar Marti
Experimentelle Physik
Universiät Ulm
![\includegraphics[width=0.5\textwidth]{kollergang.eps}](img4.gif)
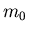 befinde sich im Abstand
befinde sich im Abstand 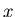 vom Ursprung auf der x-Achse. Zeigen
Sie, dass die Kraft, die von den beiden Punktmassen auf dieses Teilchen ausgeübt wird,
gegeben ist durch
vom Ursprung auf der x-Achse. Zeigen
Sie, dass die Kraft, die von den beiden Punktmassen auf dieses Teilchen ausgeübt wird,
gegeben ist durch
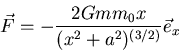
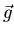 auf der x-Achse.
auf der x-Achse.
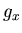 annähernd
annähernd 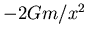 ist, wenn
ist, wenn 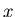 wesentlich
grösser als
wesentlich
grösser als 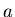 ist.
ist.
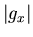 an den Punkten
an den Punkten
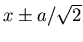 maximal ist.
maximal ist.
![\includegraphics[width=0.5\textwidth]{kollergang1.eps}](img24.gif)
![$F_x = \left[-\frac{Gm
m_0}{r_{+a}^2}\right]\frac{x}{\sqrt{x^2+a^2}}+\left[-\frac{Gm
m_0}{r_{-a}^2}\right]\frac{x}{\sqrt{x^2+a^2}}$](img51.gif)
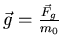 und damit
und damit
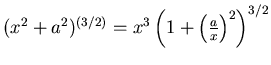
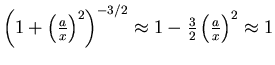
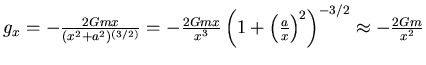
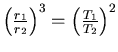 .
.
![$r_1 = \sqrt[3]{\left(\frac{T_1}{T_2}\right)^2}r_2 =
\sqrt[3]{\left(\frac{1.44\times 10^6 s}{1.53\times 10^5 s}\right)^2}4.22\times 10^8
m = 1.88\times 10^9 m$](img65.gif)
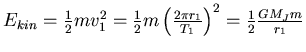
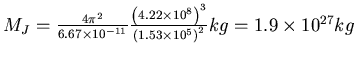
![$T_2 = \sqrt[2]{\left(\frac{a}{r_1}\right)^3}T_1 =
\sqrt[2]{\left(\frac{1.5 \times 10^{11} m}{1\times 10^{11} m}\right)^3} 2J
= 3,67 J$](img71.gif)
![$\left(\frac{v_1}{v_2}\right)^2 = \frac{r_1}{2 r_1
\left[1-\frac{r_1}{r_1+r_2}\right]} = \frac{r_1+r_2}{2 r_2} = \frac{1}{2}\left(1+\frac{r_1}{r_2}\right)$](img80.gif)