__________________________________________________________________________
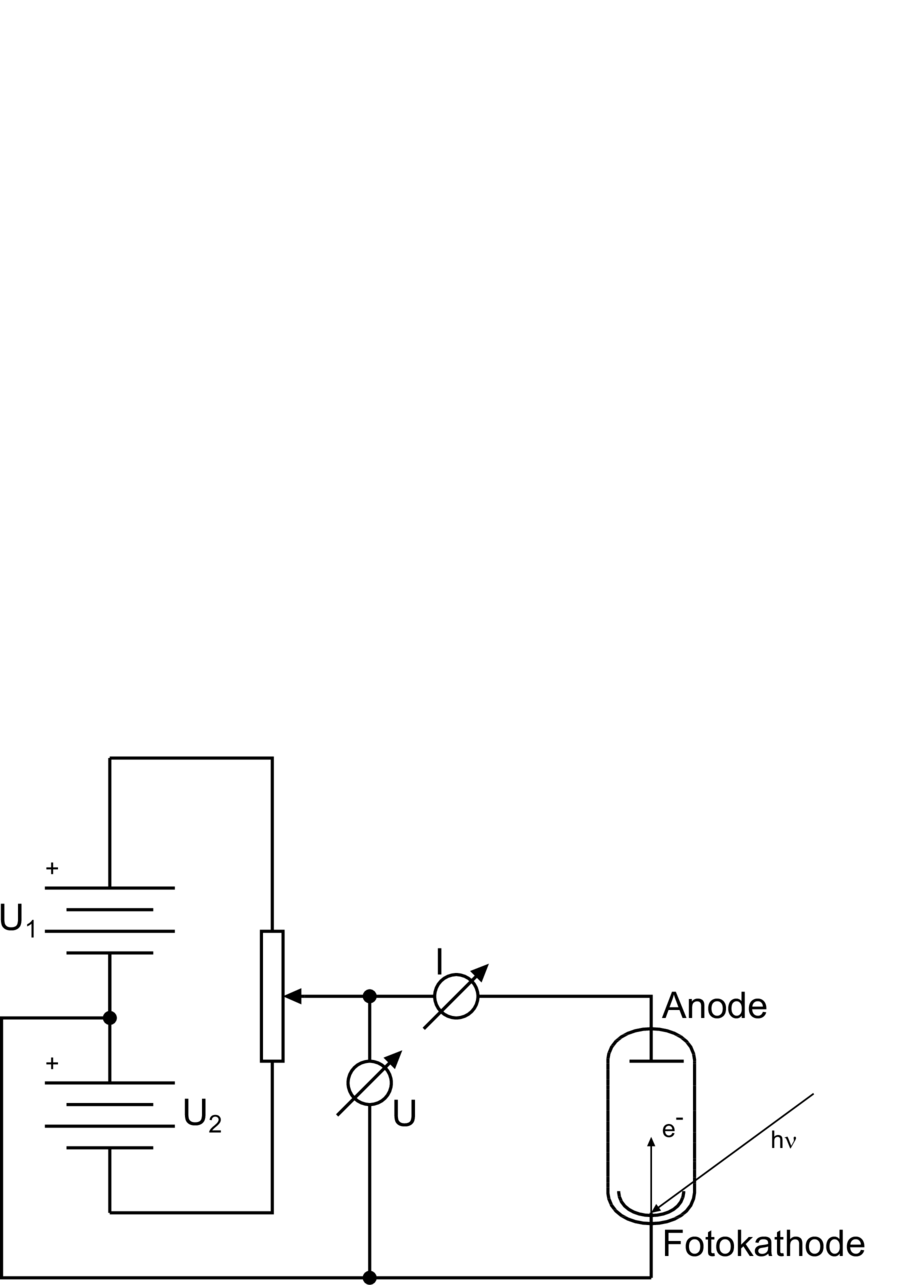
Versuchsanordnung zur Messung des Fotoeffektes
_____________________________________________________________________

__________________________________________________________________________

Versuchsanordnung zur Messung des Fotoeffektes
_____________________________________________________________________
Einsteins Erklärung des Fotoeffektes [Ein05] war einer der Meilensteine auf dem Siegeszug der Quantenmechanik. Abbildung 4.1 zeigt den Versuchsaufbau. Licht beleuchtet die Fotokathode und befreit so Elektronen aus dem Metall. Diese werden von der Anode abgesogen und erzeugen einen Strom, das Messsignal. Die beiden Spannungen U1 und U2 sind so angeordnet, dass die Anode sowohl an positiver wie auch an negativer Spannung liegen kann.
| Versuch zur Vorlesung: | |
| Fotoeffekt: qualitativ mit Aluminiumplatte (Versuchskarte AT-17) | |
_______________________________________________
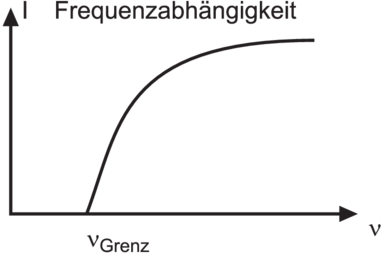
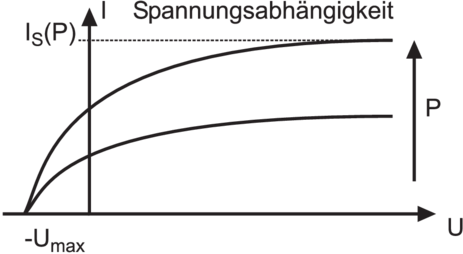
Links: Frequenzabhängigkeit des Fotostroms bei konstantem U. Rechts die Abhängigkeit von der Spannung zwischen Kathode und Anode. Negative Spannungen bedeuten, dass die Photonen die Elektronen aus der Anode herausschlagen. Die Spannung Umax ist die maximale Bremsspannung.
_____________________________________________________________________
Wenn der Fotoeffekt gemessen wird, dann können die in Abbildung 4.1 dargestellten Beobachtungen gemacht werden. Bei konstanter Anodenspannung U muss das Licht eine gewisse Frequenz überschreiten (oder eine bestimmte Wellenlänge unterschreiten), damit ein Strom fliesst. Wenn die Spannung U variiert wird, dann nimmt der Strom mit zunehmender Spannung U monoton zu. Unter einer negativen Spannung −Umax fliesst kein Strom. Wird nun die Bestrahlungsstärke erhöht, dann nimmt der Strom zu, aber die Grenzspannung −Umax ändert sich nicht.
__________________________________________________________________________
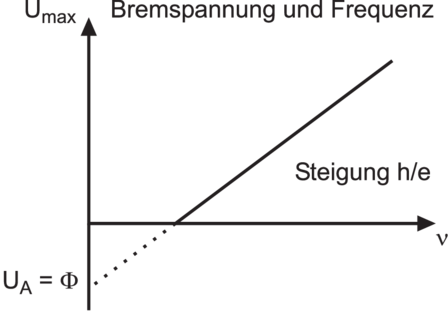
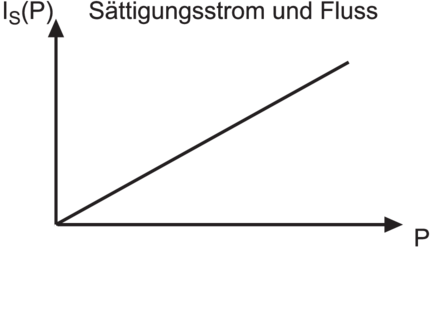
Links: Abhängigkeit der Bremsspannung Umax von der Frequenz ν. UA = Φ heisst die Austrittsarbeit. Rechts die Abhängigkeit des Sättigungsstromes IS vom Photonenfluss P = Φ.
_____________________________________________________________________
Abbildung 4.1 zeigt, dass die Bremsspannung −Umax von der Frequenz oder der Wellenlänge des eingestrahlten Lichtes abhängt. Zusammen mit der Tatsache, dass −Umax unabhängig von der Beleuchtungsstärke ist, bedeutet das, dass die Energie in Quanten fliesst mit einer maximalen Energie pro Quant. Die Beobachtung in Abbildung 4.1 ,dass bei einer bestimmten Spannung U > −Umax der Strom proportional zur Strahlungsleistung oder Beleuchtungsstärke ist, stützt diese Ansicht.
Albert Einstein formulierte darauf aufbauend in seiner mit dem Nobelpreis gewürdigten Arbeit:
|
________________________________________________________________
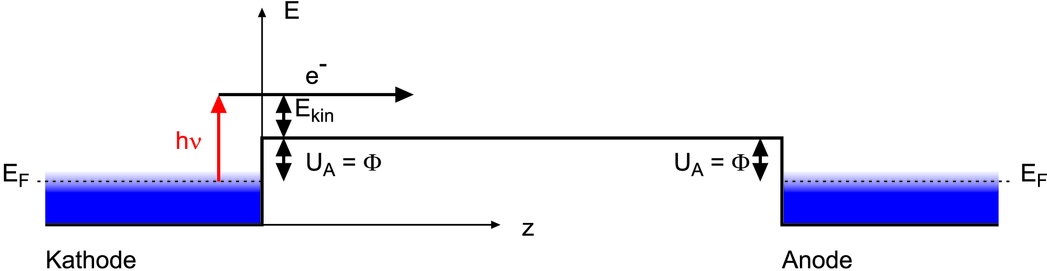
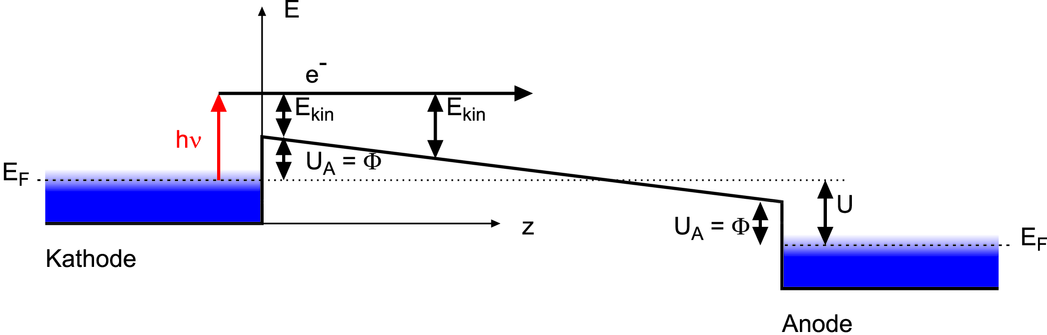
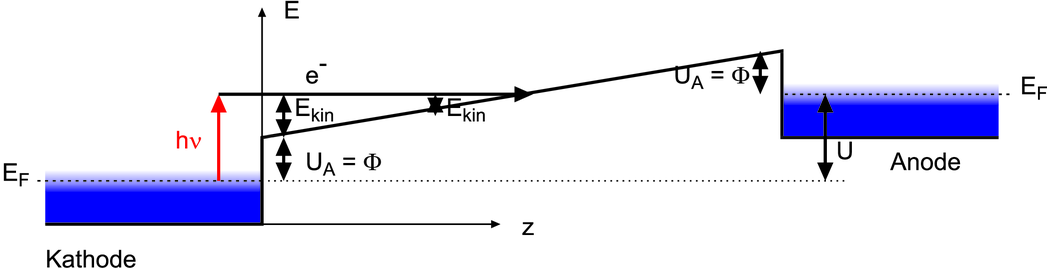
Oben: Energieschema des Fotoeffekts ohne angelegte Spannung, Mitte: mit der Anode positiv gegen die Photokathode, unten mit der „Anode“negativ gegen die „Photokathode“. Die Energiekoordinate muss man sich als vierte (ohne Zeit) oder fünfte Koordinate eines Punktes vorstellen. Die Grösse EF ist die Fermi-Energie und steht bei einer Temperatur T > 0 auch für das chemische Potential μ.a
_______________________________________________________________________________________
Abbildung 4.1 zeigt, im Vorgriff auf die Vorlesung zur
Physik der kondensierten Materie, ein Bänderschema des
Fotoeffektes. Es ist bekannt, dass bei der Temperatur T die
thermische Energie sich nach Boltzmann wie exp 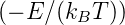 verhält. Damit also Elektronen bei Raumtemperatur im
Metall bleiben, muss eine Energiebarriere zum Verlassen des
Festkörpers existieren. Die Höhe dieser Barriere wird
Austrittsarbeit Φ genannt.
verhält. Damit also Elektronen bei Raumtemperatur im
Metall bleiben, muss eine Energiebarriere zum Verlassen des
Festkörpers existieren. Die Höhe dieser Barriere wird
Austrittsarbeit Φ genannt.
Elektronen, die das Metall verlassen, haben die kinetische Energie:
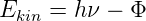 | (4.1) |
Da die kinetische Energie der Elektronen im Metall nach Boltzmann bei einer endlichen Temperatur über einen Energiebereich verteilt, also ausgeschmiert, ist, ist auch die kinetische Energie der Elektronen Ekin ausgeschmiert. Da die Emissionsrichtung der Elektronen um die Senkrechte zur Oberfläche verteilt ist, wird die Energieverteilung der Elektronen noch weiter verändert.
| Versuch zur Vorlesung: | |
| Interferenz am Doppelspalt: mit einzelnen Photonen (Versuchskarte AT-50) | |
_______________________________________________
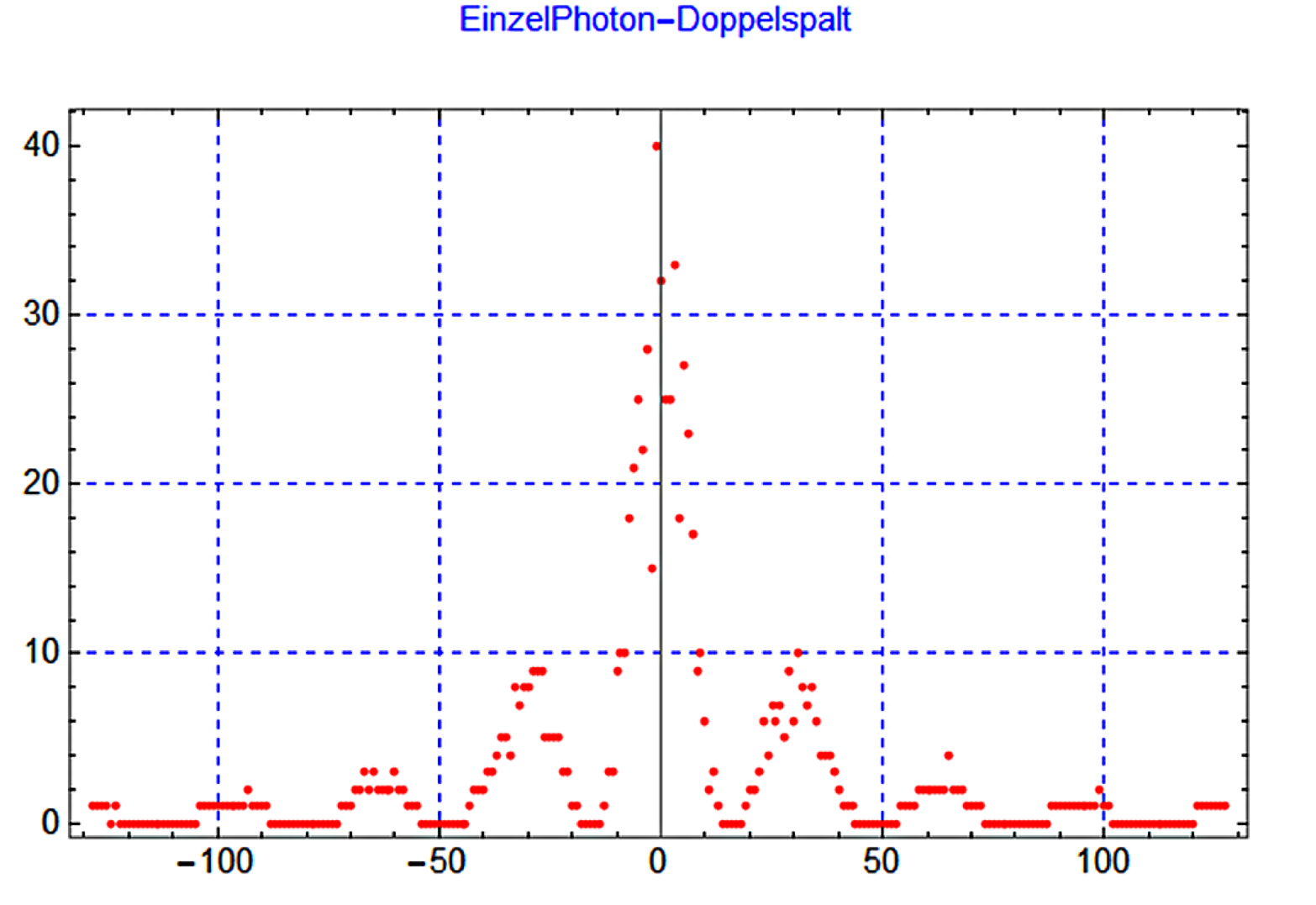
Simulation eines Einzelphotonen-Doppelspaltexperimentes. (Animation: https://youtu.be/ZYwxhpZ_D1k)
_____________________________________________________________________
| Versuch zur Vorlesung: | |
| Doppelspalt: Interferenz mit polarisiertem Licht (Versuchskarte AT-51) | |
Die Versuche mit dem Doppelspalt zeigen, dass die statistische Interpretation des Energietransportes von Einstein korrekt war.
Wenn die Lichtintensität niedrig ist, verhält sich Licht wie ein Strom von Teilchen. Wenn die Auftreffwahrscheinlichkeit in Abhängigkeit des Ortes über eine längere Zeit aufsummiert wird, ergeben sich Interferenzmuster, wie sie von der Wellentheorie vorausgesagt werden.
| Photonen haben wie alle anderen Objekte mit Energie sowohl einen Teilchencharakter wie auch einen Wellencharakter. Der Wellencharakter gibt die Wahrscheinlichkeit an, ein Objekt an einem bestimmten Ort zu einer bestimmten Zeit zu finden. Die Energie pro Objekt ist quantisiert. |
Licht ist ein Strom von Energiepaketen mit einer Richtung und einer Geschwindigkeit, der (vom Medium abhängigen) Lichtgeschwindigkeit. Aus der Mechanik weiss man, dass eine Änderung der kinetischen Energie durch eine Kraft erreicht wird. Genauso benötigt man eine Kraft zur Änderung der Richtung. Eine Kraft ist, auch relativistisch, eine Änderung des Impulses pro Zeit.
Photonen sind Teilchen mit einer kinetischen Energie
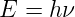 | (4.2) |
Konsequenterweise haben Photonen dann auch einen Impuls. Um die Beziehung zwischen dem Impuls des Lichtes und seiner Energie zu bestimmen, verwenden wir die relativistische Energie-Impuls-Beziehung
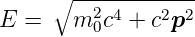 | (4.3) |
Da im Vakuum die Geschwindigkeit des Lichtes die Vakuumlichtgeschwindigkeit ist, gilt für alle Photonen dass die Ruhemasse null sein muss
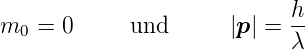 | (4.4) |
Aus Gleichung (4.3) und Gleichung (4.2) bekommt man
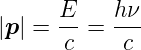 | (4.5) |
Damit ist die Impulsänderung bei Absorption und Reflexion
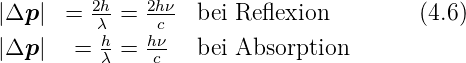
Daraus ergibt sich bei der Reflexion der mechanische Druck auf die Fläche ΔA
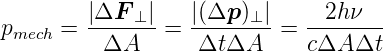
Mit 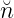 = Anzahl Teilchen∕Zeit bekommen wir
= Anzahl Teilchen∕Zeit bekommen wir
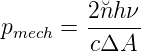
Die Bestrahlungsstärke oder Intensität ist mit der Leistung ΔP
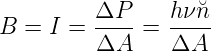
Schliesslich erhalten wir
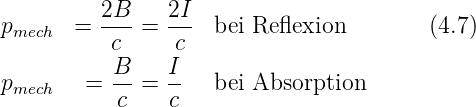
Abbildung 4.1.1 zeigt eine Apparatur zur Messung des Lichtdruckes auf mikroskopische einseitig eingespannte Balken[MRH+92].
__________________________________________________________________________
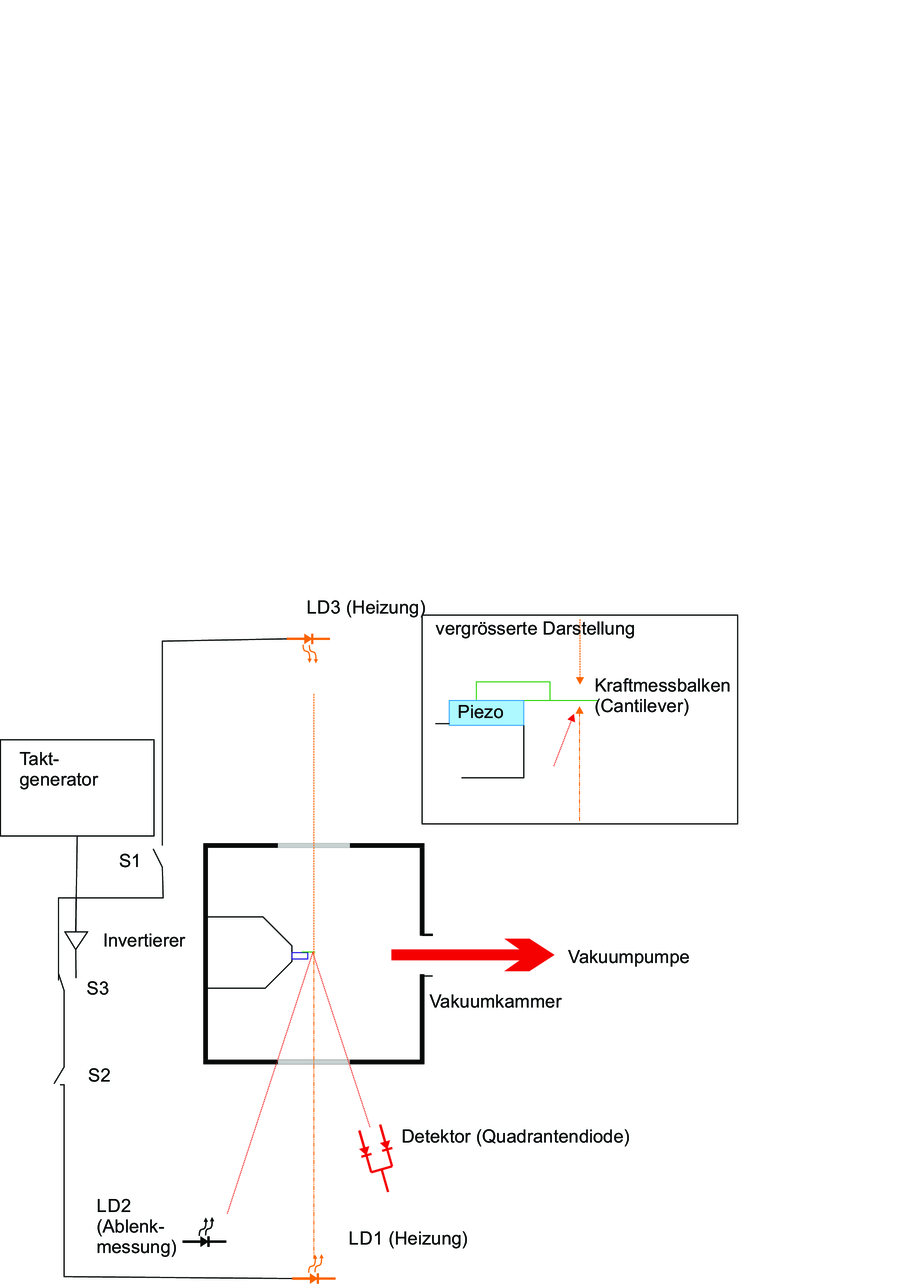
Aufbau einer Apparatur zum Messen des Lichtdrucks.
_____________________________________________________________________
Das gleiche Ergebnis hätten wir auch erhalten, wenn wir die Volumenenergiedichte des Lichtfeldes vor dem Spiegel oder vor dem Absorber berechnet hätten. Beim Absorber fliesst nur ein Lichtstrom auf ihn zu, bei der Reflexion gibt es zwei gegenläufige Lichtströme, also auch die doppelte Energiedichte. Konkret lautet die klassische Rechnung aus der Elektrizitätslehre so:
Man beginnt mit dem Vektor des Energieflusses, dem Poyntingvektor.
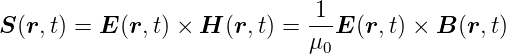
Hier ist der Poyntingvektor gleich der Strahlungsstromdichte
(3.1), also  =
= 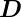 . Weiter ist die Intensität gleich dem Betrag
der Strahlungsstromdichte, also I =
. Weiter ist die Intensität gleich dem Betrag
der Strahlungsstromdichte, also I = 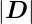 . Druck ist das
Gleiche wie Energie pro Volumen oder Energiedichte. Wenn
die Energiedichte ϱE sich mit einer Geschwindigkeit c bewegt,
ist der Poyntingvektor S = D.
. Druck ist das
Gleiche wie Energie pro Volumen oder Energiedichte. Wenn
die Energiedichte ϱE sich mit einer Geschwindigkeit c bewegt,
ist der Poyntingvektor S = D.
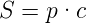
und damit der Druck oder die Energiedichte ϱE auf eine senkrecht dazu stehende Ebene
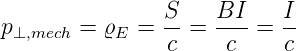 | (4.8) |
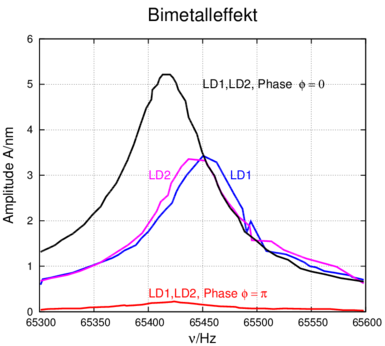
Bei isotroper Strahlung ist der Druck
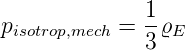 | (4.9) |
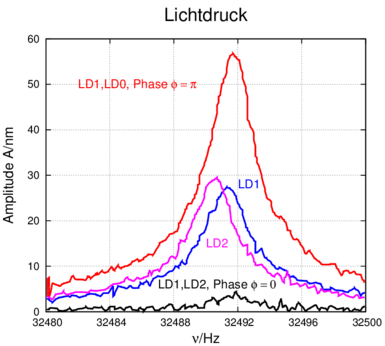
Die beiden folgenden Abbildungen zeigen Messungen mit der Apperatur aus Abbildung 4.1.1.
__________________________________________________________________________
Messung der lichtinduzierten Kräfte. Die Amplitude ist maximal, wenn die Impulsmodulation maximal ist.
_____________________________________________________________________
_____________________________________________________________________
Kontrolle: Mit einer Metallbeschichtung ist die Amplitude maximal, wenn die thermische Modulation maximal ist. Man beachte die Verschiebung zu kleineren Frequenzen bei sehr hohen Amplituden.
_____________________________________________________________________
Es wurden zwei gegenläufige Laserstrahlen verwendet. Im Falle der Abbildung 4.1.1 wurden die Strahlen wechselseitig ein- und ausgeschaltet, so dass der Kraftwechsel maximal wurde und gleichzeitig der Energieeintrag über die Zeit konstant war. Die gemessene Kurve ist eine Resonanzkurve als Funktion der Schaltfrequenz. Die Resonanzkurve zeigt die mechanische Kraft des Lichtes sehr schön. Zur Kontrolle wurden in der Abbildung 4.1.1 die beiden gegenläufigen Laserstrahlen gleichzeitig ein- und ausgeschaltet. Damit ist die ponderomotorische Kraft des Lichtes konstant null, aber der Energieeintrag wird maximal moduliert. Mit dieser Messung kann gezeigt werden, dass in Abbildung 4.1.1 wirklich mechanische Effekte des Lichtes bestimmt wurden.
Schliesslich kann aus den obigen Messungen und Überlegungen eine dynamische Masse des Photons bestimmt werden. Aus
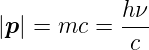
bekommen wir
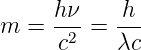 | (4.10) |
Beispiel: Mit λ = 500 nm ist mphoton = 4.4·10−36 kg.
Beim Compton-Effekt wird Licht an einem Teilchen gestreut. Im Originalversuch von Arthur Compton [Com23a] wurden Photonen an Elektronen gestreut.
__________________________________________________________________________

_____________________________________________________________________
In Abbildung 4.1.1.1 ist die experimentelle Anordnung gezeigt. Der Winkel zwischen der einfallenden Lichtwelle (oder, was äquivalent dazu ist, dem Impuls des einfallenden Photons) und der gestreuten Welle sei 𝜃. Die Masse des Elektrons sei me. Bei jeder Kollision zwischen zwei Teilchen wird Energie ausgetauscht. Dabei ändert sich der Impuls des leichteren Teilchens, hier also des Photons, besonders stark. Mit Gleichung (4.5) ändert sich also auch die Frequenz und damit die Wellenlänge und die Energie.
Wir haben ein schiefwinkliges Dreieck mit den Seiten hν, hν′ und mev′ und dem mev′ gegenüberliegenden Winkel 𝜃. Aus dem Cosinussatz wissen wir, dass c2 = a2 + b2 − 2ab cos(γ) ist. Weiter ist nach den Additionstheoremen cos(γ) = 1 − 2 sin 2(γ∕2). Wir können also aus der Impulserhaltung schreiben:
Aus der Energieerhaltung folgt weiter
Die Kombination von (4.11) und (4.13) ergibt
Mit 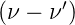 2 «
2 «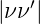 , d.h. wenn der relative Energieverlust
des Photons beim Stoss klein ist, ergibt sich
, d.h. wenn der relative Energieverlust
des Photons beim Stoss klein ist, ergibt sich
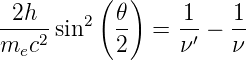 | (4.16) |
und mit λ = c∕ν erhalten wir die Gleichung für die
Compton-Streuung
|
und die
Compton-Wellenlänge
|
Abbildung 4.1.1.1 zeigt Messungen der Compton-Streuung bei unterschiedlichen Streuwinkeln. Die horizontale Achse ist die Wellenlänge.
__________________________________________________________________________
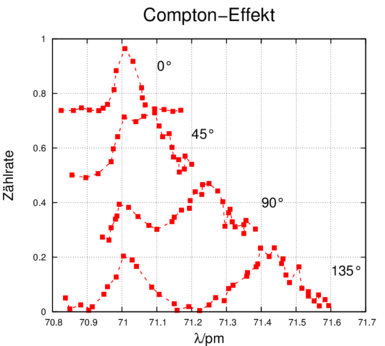
Compton-Effekt bei vier Streuwinkeln, skizziert nach [Com23b]
_____________________________________________________________________
Beim Mössbauer-Effekt [Möß58] wird die Emission und die Absorption von γ-Quanten aus Kernen beobachtet. γ-Quanten sind hochenergetische Photonen. Durch die hohe Masse der Kerne und deren Einbindung in ein Kristallgitter ist die Energie der γ-Quanten sehr wohl definiert (d.h. die Streuung der Energie ist minimal.). Das hängt auch damit zusammen, dass die Energieniveaus in Kernen sehr scharf definiert sind.
__________________________________________________________________________

Impulserhaltung bei der Emission eines γ-Quants.
_____________________________________________________________________
Bei der Emission eines γ-Quants sind Energie und Impuls erhalten. Sei hν die Energie eines γ-Quants, wenn der Kern bei der Emission in Ruhe bleibt. Das Emissions- und das Absorptionsspektrum müssen überlappen (siehe Abbildung 4.1.1.2).
__________________________________________________________________________
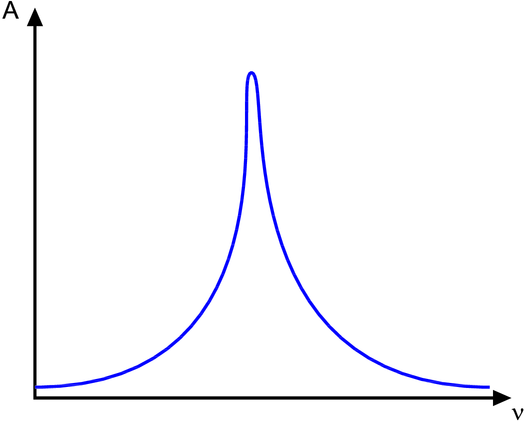
Absorptions- oder Emissionspektrum für ein γ-Quant. Nur wenn die Frequenz des ankommenden γ-Quants im Bereich der Absorptionslinie liegt, kann das Quant absorbiert werden.
_____________________________________________________________________
Wegen der Impulserhaltung kann man für den Impuls des Kernes vor der Emission pk und nach der Emission pk′ schreiben:
Mit mk der Masse des Kerns und mit (4.19) wird seine kinetische Energie nach dem Stoss
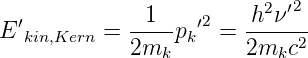 | (4.20) |
Die Energie der Anregung hν ist im Ruhesystem des noch nicht bewegten Kerns gegeben. Erst nach der Anregung muss die Impulserhaltung erfüllt sein. Dann folgt aus der Energieerhaltung.
__________________________________________________________________________
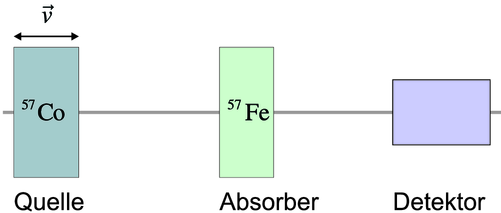
Experimenteller Aufbau der Mössbauer-Spektroskopie
_____________________________________________________________________
Um den Rückstossimpuls des Kerns zu minimieren, erfand Mössbauer den folgenden nobelpreiswürdigen Trick: Die γ-Quanten emittierenden Atome wurden in einen Kristall eingebettet. Damit wird der Rückstossimpuls des Kerns von den anderen Atomen im Gitter aufgenommen (Thema der Vorlesung Festkörperphysik) und der Kern bleibt in Ruhe. Die Breite der Linien wird dann so schmal, dass normale Detektoren sie nicht auflösen können. Mössbauer verwendete dann eine ähnliche Versuchsanordnung wie in Abbildung 4.1.1.2 gezeigt. Die Energie der Photonen ist nun so gut definiert, dass die relativistische Frequenzverschiebung bei Geschwindigkeiten von mm/s ausreicht, um die Absorptionslinie abzutasten.
__________________________________________________________________________
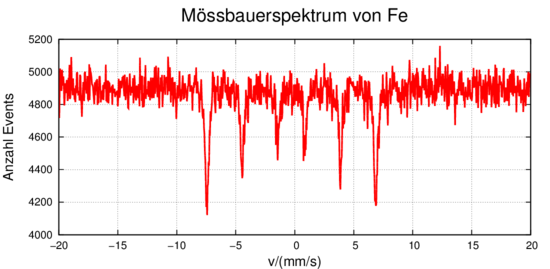
Mössbauerspektrum von 57Fe , gemessen von Dr. M. Gonçalves.
_____________________________________________________________________
Abbildung 4.1.1.2 zeigt eine Messung eines Mössbauerspektrums von 57Fe. Die beiden Kerne mit der gleichen Barionenzahl (Summe aus Neutronen und Protonen) haben eine ähnliche Niveaustruktur. 57Co ist instabil, 57Fe arbeitet als Absorber. Durch den Einbau in einen Festkörper sind die Linienbreiten sehr klein. Deshalb wird die Quelle (oder der Absorber) gegen den Absorber (oder der Quelle) bewegt. Angezeigt ist die Geschwindigkeit der 57Co -Quelle und die Anzahl der detektierten Photonen nach einer sehr langen Messung (> 24 h). Die Geschwindigkeit ist linear, das Spektrum mit sechs Linien (Zeemann-Aufspaltung) sollte bei einer perfekten Messapparatur symmetrisch um v = 0 angeordnet sein.
 Lizenzinformationen
Lizenzinformationen