__________________________________________________________________________
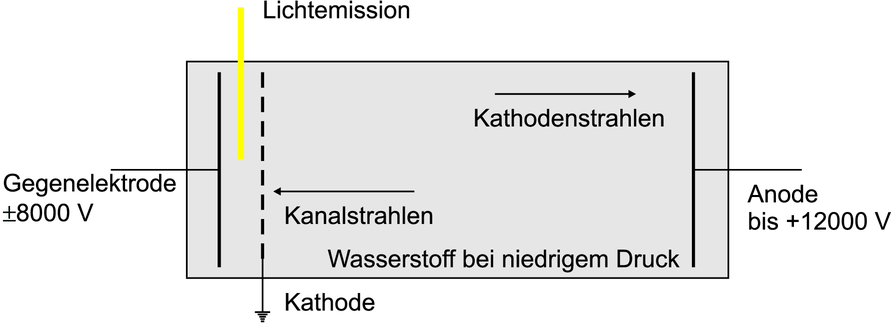
Apparatur zur Beobachtung des Starkeffektes.
_____________________________________________________________________

__________________________________________________________________________

Apparatur zur Beobachtung des Starkeffektes.
_____________________________________________________________________
In der Apparatur nach Abbildung 6.6 werden Elektronen von der Kathode zur Anode mit Spannungen bis zu 12000 V beschleunigt. Diese Elektronen können das Hintergrundgas Wasserstoff ionisieren. Damit werden sie als „Kanalstrahlen“ zur Kathode hin beschleunigt. Durch die mechanische Trägheit treten sie durch die Kathode hindurch und werden neutralisiert, das heisst wieder mit einem Elektron versehen. Im starken elektrischen Feld zwischen Kathode und Gegenelektrode beobachtet man eine Aufspaltung der Spektrallinien, den Starkeffekt.
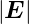 proportionale Aufspaltung der ℓ ⇔ 0-Terme des
Wasserstoffspektrums. Dieser Effekt wird der lineare
Starkeffekt, genannt.
proportionale Aufspaltung der ℓ ⇔ 0-Terme des
Wasserstoffspektrums. Dieser Effekt wird der lineare
Starkeffekt, genannt.
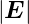 2 proportionale Aufspaltung, den quadratischen
Starkeffekt
2 proportionale Aufspaltung, den quadratischen
Starkeffekt Der Starkeffekt entsteht, weil das elektrische Feld 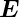 in Atomen
ein elektrisches Dipolmoment (Proportionalitätskonstante ist
die Polarisierbarkeit α des Atoms)erzeugt.
in Atomen
ein elektrisches Dipolmoment (Proportionalitätskonstante ist
die Polarisierbarkeit α des Atoms)erzeugt.
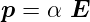 | (6.1) |
Dieser elektrische Dipol hat im externen elektrischen Feld
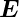 die potentielle Energie:
die potentielle Energie:
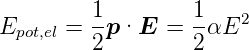 | (6.2) |
Diese quadratische potentielle Energie führt in der Schrödingergleichung auf den quadratischen Starkeffekt. Um den linearen Starkeffekt zu verstehen werden die Methoden der Quantenmechanik benötigt.
__________________________________________________________________________
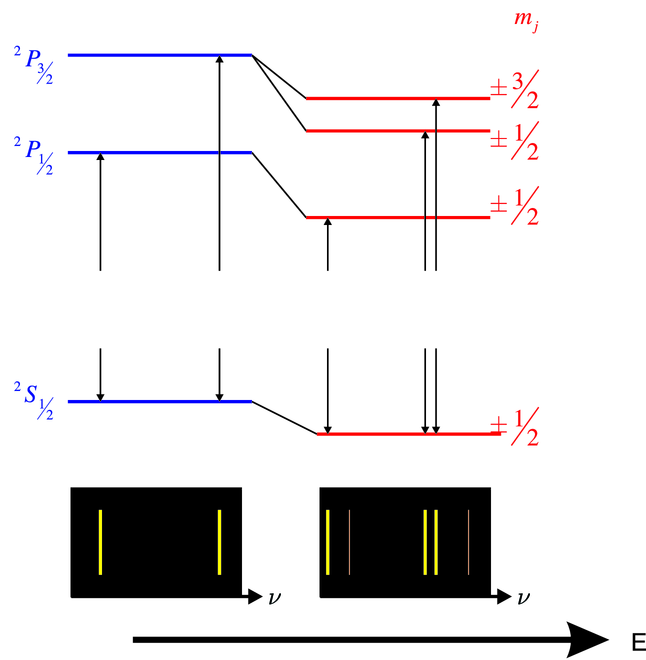
Energieniveauschema des Natriumdubletts im elektrischen Feld.
_____________________________________________________________________
Abbildung 6.6.1 zeigt in einem Jablonski-Diagramm den
Stark-Effekt beim Na-Dublett mit den Übergängen
2
P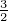 ↔2S
↔2S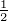 und 2P
und 2P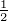 ↔2S
↔2S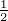 . Im elektrischen Feld lautet der
Hamiltonoperator für den Starkeffekt
. Im elektrischen Feld lautet der
Hamiltonoperator für den Starkeffekt
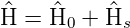 | (6.3) |
wobei 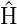 0 der Hamiltonoperator des Atoms im felfdfreien
Raum und
0 der Hamiltonoperator des Atoms im felfdfreien
Raum und 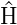 S der im elektrischen Feld dazukommende
Störterm ist.
S der im elektrischen Feld dazukommende
Störterm ist.
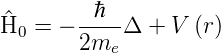 | (6.4) |
Die Kraft auf ein Elektron im elektrischen Feld ist
−e 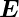 . Dies führt zu einer potentielle Energie der Störung
V s = e
. Dies führt zu einer potentielle Energie der Störung
V s = e 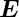 ·
·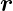 . Diese Störung kann als Taylorreihe geschrieben
werden:
. Diese Störung kann als Taylorreihe geschrieben
werden:
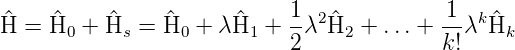 | (6.5) |
Für kleine Störungen kann man nach der ersten Ordnung abbrechen
 | (6.6) |
Wir nehmen an, dass die Schrödingergleichung ohne den Störterm gelöst sei.
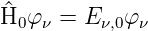 | (6.7) |
Eν,0 sei der ν-te Eigenwert. Der Index 0 deutet auf das ungestörte Problem. Wir nehmen weiter an, dass alle Eν,0 voneinander verschieden seien. Weiter nehmen wir an, dass die resultierende Wellenfunktion eine Linearkombination der ursprünglichen Wellenfunktionen sei.
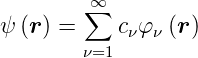 | (6.8) |
Dies ist möglich, weil die Lösungen der ungestörten Schrödingergleichung ein vollständiges Funktionssystem bilden. Wir können also schreiben:
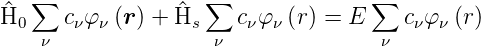 | (6.9) |
wobei
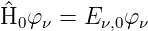 | (6.10) |
ist. Die Lösungen φν sind normiert:
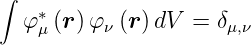 | (6.11) |
Dann sind die Matrixelemente des Hamiltonoperators der Störung
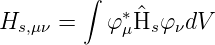 | (6.12) |
Gleichung (6.9) wird damit
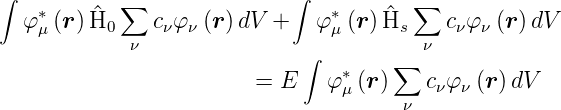 | (6.13) |
Wir setzen Gleichung (6.10) in Gleichung (6.13) ein und erhalten
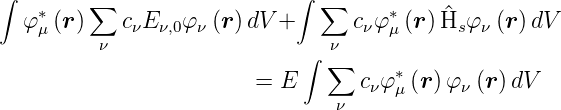 | (6.14) |
Diese Gleichung muss für jeden Index μ gelten, wobei die Normierung aus Gleichung (6.11) berücksichtigt werden muss
Wenn keine Störung vorhanden ist, ist λ = 0 und
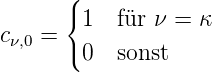 | (6.16) |
wobei κ der Index des Ausgangszustandes sei, also
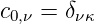 | (6.17) |
Damit ist die Reihenentwicklung
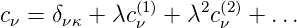 | (6.18) |
Für die Energie bekommt man
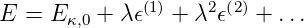 | (6.19) |
Diese beiden Gleichungen kann man in Gleichung (6.14) einsetzen
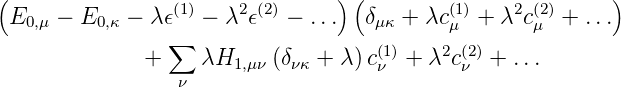 | (6.20) |
Wir fordern nun, dass die Koeffizienten zu allen Potenzen
von λ jeweils getrennt verschwinden. Für die nullte Potenz,
die ungestörte Schrödingergleichung gilt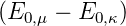 δμκ = 0, da entweder δμκ = 0 ist oder die
Koeffizienten sind gleich und die Klammer ist null.
δμκ = 0, da entweder δμκ = 0 ist oder die
Koeffizienten sind gleich und die Klammer ist null.
Für die erste Potenz von λ erhalten wir
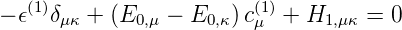 | (6.21) |
Wenn die Indizes gleich sind, also für μ = κ, folgt aus Gleichung (6.21)
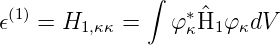 | (6.22) |
oder
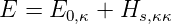 | (6.23) |
Hs,κ,κ ist das Matrixelement, also eine Zahl und kein Operator. Für den Fall μ ⇔ κ erhält man aus Gleichung (6.21)
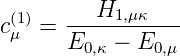 | (6.24) |
Aus der Normierungsbedingung Gleichung (6.11) folgt, dass
cκ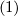 = 0 ist. Damit wird
= 0 ist. Damit wird
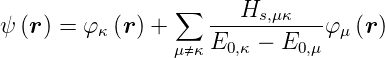 | (6.25) |
In 2. Ordnung erhalten wir
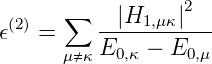 | (6.26) |
Also ist
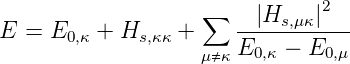 | (6.27) |
Beim Wasserstoffatom folgt aus den Auswahlregeln, dass
Hs,κκ = 0 ist. Dann ist V ≈ 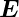 und damit Hs ≈
und damit Hs ≈ 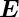 2.
Wasserstoff zeigt wie andere Atome den quadratischen
Starkeffekt.
2.
Wasserstoff zeigt wie andere Atome den quadratischen
Starkeffekt.
Den linearen Starkeffekt erhält man, wenn man entartete Zustände mit einer Multiplizität grösser eins betrachtet. Dann versagt das vorherige Verfahren. Wenn für zwei Indizes μ ⇔ κ die Energiedifferenz
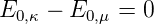 | (6.28) |
nennt man diese beiden Zustände entartete Zustände. Die Forderung
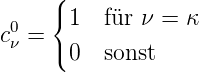 | (6.29) |
kann man nicht erfüllen. Wir setzen
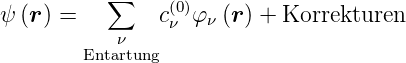 | (6.30) |
Dieses Gleichungssystem ist lösbar, wenn Determinante
 = 0 ist.
= 0 ist.
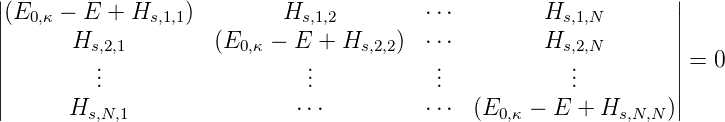 | (6.31) |
Beispiel Wir betrachten den 1. angeregten Zustand von H mit φn,l,m. Die Hauptquantenzahl sei n = 2. Wir verwenden die folgenden Definitionen für ν
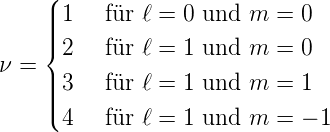 | (6.32) |
und erhalten
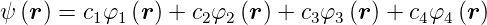 | (6.33) |
mit
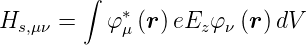 | (6.34) |
wobei das 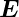 −Feld in die z-Richtung zeigt.
−Feld in die z-Richtung zeigt.
Nach den Auswahlregeln für optische Übergänge verschwinden alle Hs,μν bis auf Hs,1,2 und Hs,2,1. Dieses Matrixelement hat den Wert
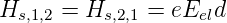 | (6.35) |
wobei Eel das elektrische Feld ist. Wir untersuchen den Fall mit N = 4, beachten, dass κ = 2 oder κ = 1 sein könnte (entartete Energien), und erhalten zuerst
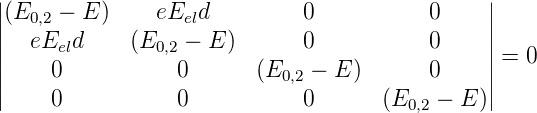 | (6.36) |
und das dazugehörige lineare Gleichungssystem
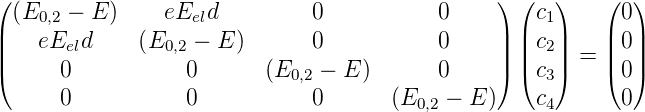 | (6.37) |
Ausgeschrieben lautet das System
Aus den Gleichungen (6.38a) und (6.38b) folgt
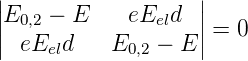 | (6.39) |
Die Energien sind
wobei für die Koeffizienten gilt
Aus den Gleichungen (6.38c) und (6.38d) erhalten wir
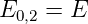 | (6.43) |
Dieser lineare Starkeffekt wird nur bei H beobachtet, da nur bei H ℓ entartet ist. Bei allen anderen Atomen sind die Energieniveaus zu ℓ ⇔ ℓ′ unterschiedlich.
 Lizenzinformationen
Lizenzinformationen