__________________________________________________________________________
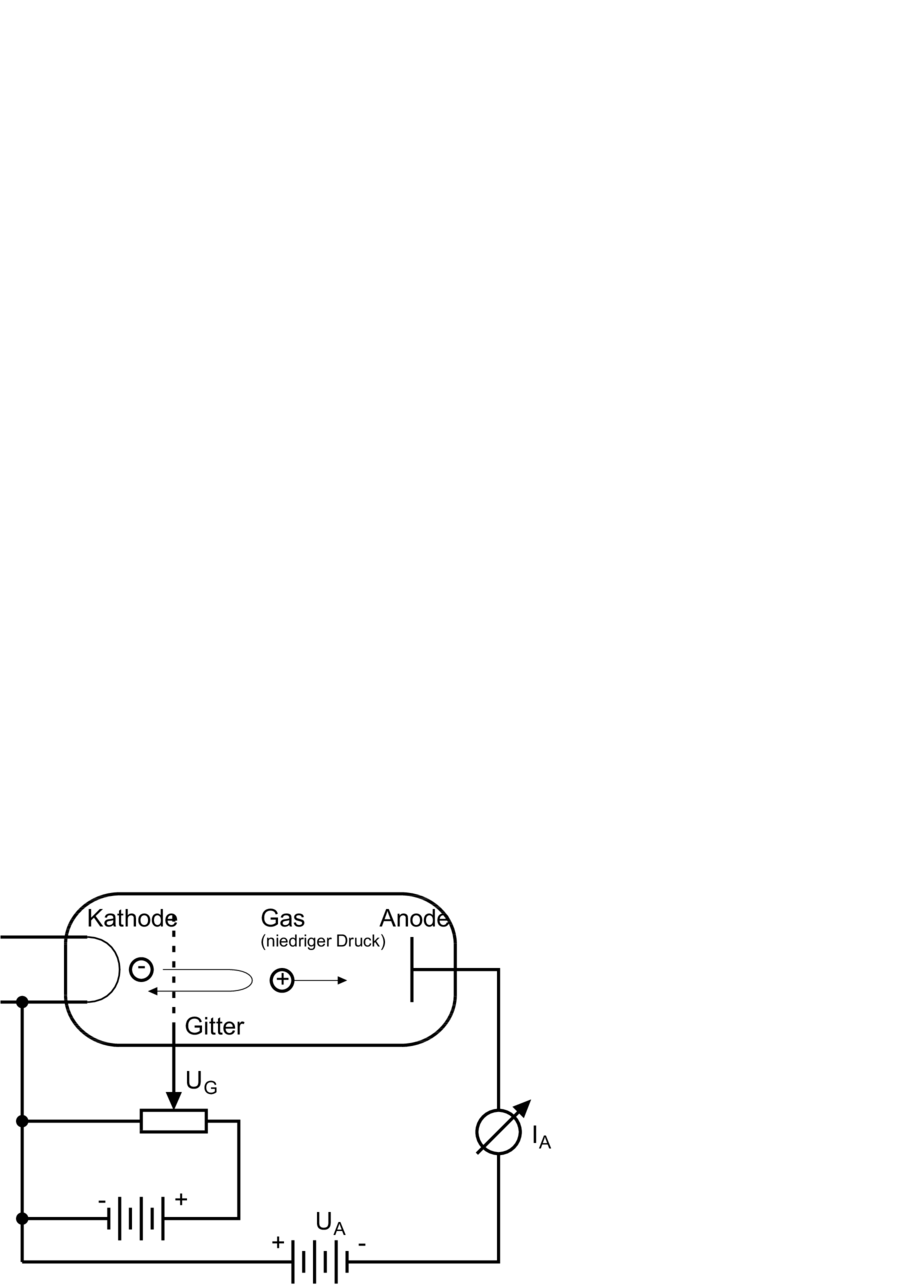
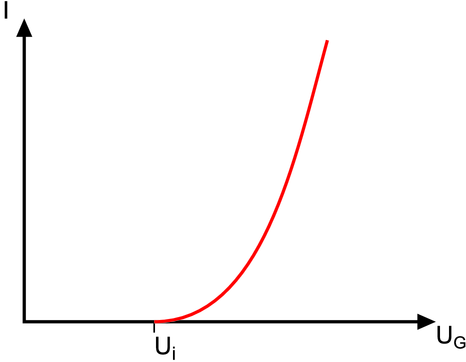
Ionisierung eines Gases. Links ist der Versuchsaufbau, rechts die Kennlinie.
_____________________________________________________________________

| Versuch zur Vorlesung: | |
| Franck-Hertz-Versuch (Versuchskarte AT-7) | |
Gegen Ende des 19. Jahrhunderts wurde festgestellt, dass beschleunigte Elektronen verdünnte Gase zum Leuchten bringen. Glimmlampen verwenden diesen Effekt. Philip Lenard, ein ungarischstämmiger Physiker, der sich später der Nazi-Ideologie näherte, beschrieb 1902 eine Versuchsanordnung (siehe Abbildung 6.2), mit der der Effekt quantitativ untersucht werden konnte.
__________________________________________________________________________


Ionisierung eines Gases. Links ist der Versuchsaufbau, rechts die Kennlinie.
_____________________________________________________________________
Elektronen werden durch die Beschleunigungsspannung UG
(Gitterspannung) von der Kathode zum Gitter beschleunigt.
Die schnellen Elektronen verfehlen meistens das Gitter und
dringen in den Raum zwischen dem Gitter und der negativ
polarisierten Elektrode ein. Dort werden sie abgebremst und
zum Gitter zurück beschleunigt. Abbildung 6.2 zeigt die
Energieverhältnisse. Wenn die ortsabhängige kinetische
Energie der Elektronen den Wert eUi übersteigt, können die
Elektronen die Gasmoleküle (zum Beispiel Hg) ionisieren. Die
positiven Ionen werden durch die negative Spannung UA zur
Anode beschleunigt. Wenn 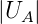 >
> 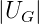 ist, werden die Ionen
angezogen und die Elektronen abgestossen. Die Kennlinie
zeigt, dass es für die Ionisation eine Schwelle eUi gibt, die von
der Atom- oder Molekülsorte abhängt.
ist, werden die Ionen
angezogen und die Elektronen abgestossen. Die Kennlinie
zeigt, dass es für die Ionisation eine Schwelle eUi gibt, die von
der Atom- oder Molekülsorte abhängt.
__________________________________________________________________________
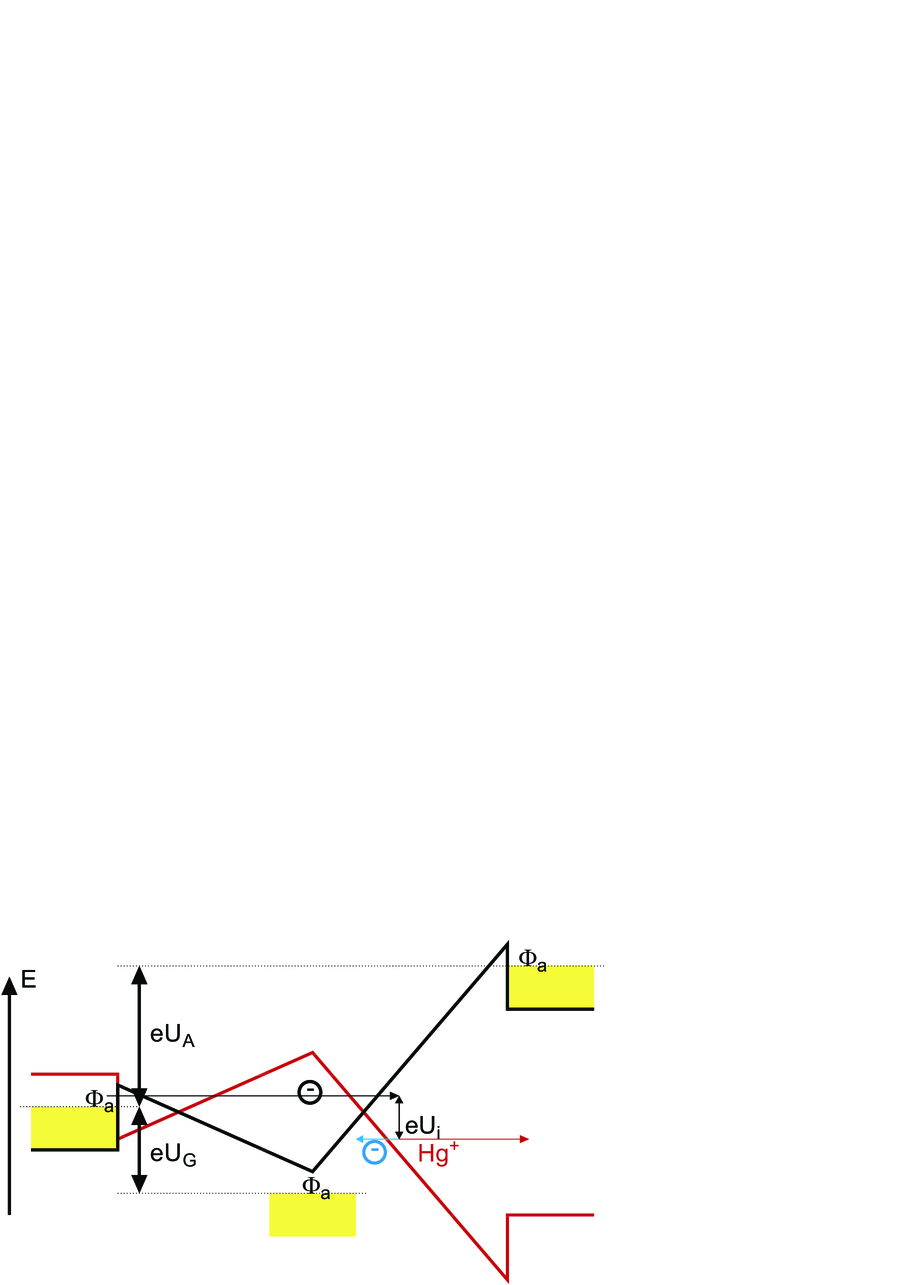
Energieverhältnisse beim Ionisierungs-Versuch. Die Energiekurven in Schwarz sind für Elektronen gezeichnet. Rot sind die Energieverhältnisse für positive Ionen angegeben, hier einfach positiv geladenes Hg+.
_____________________________________________________________________
Beim Versuch von Franck und Hertz aus dem Jahre 1913 ([FH14]) wird der nach der Ionisation übrig bleibende Strom zwischen Gitter und Anode gemessen.
__________________________________________________________________________
_____________________________________________________________________
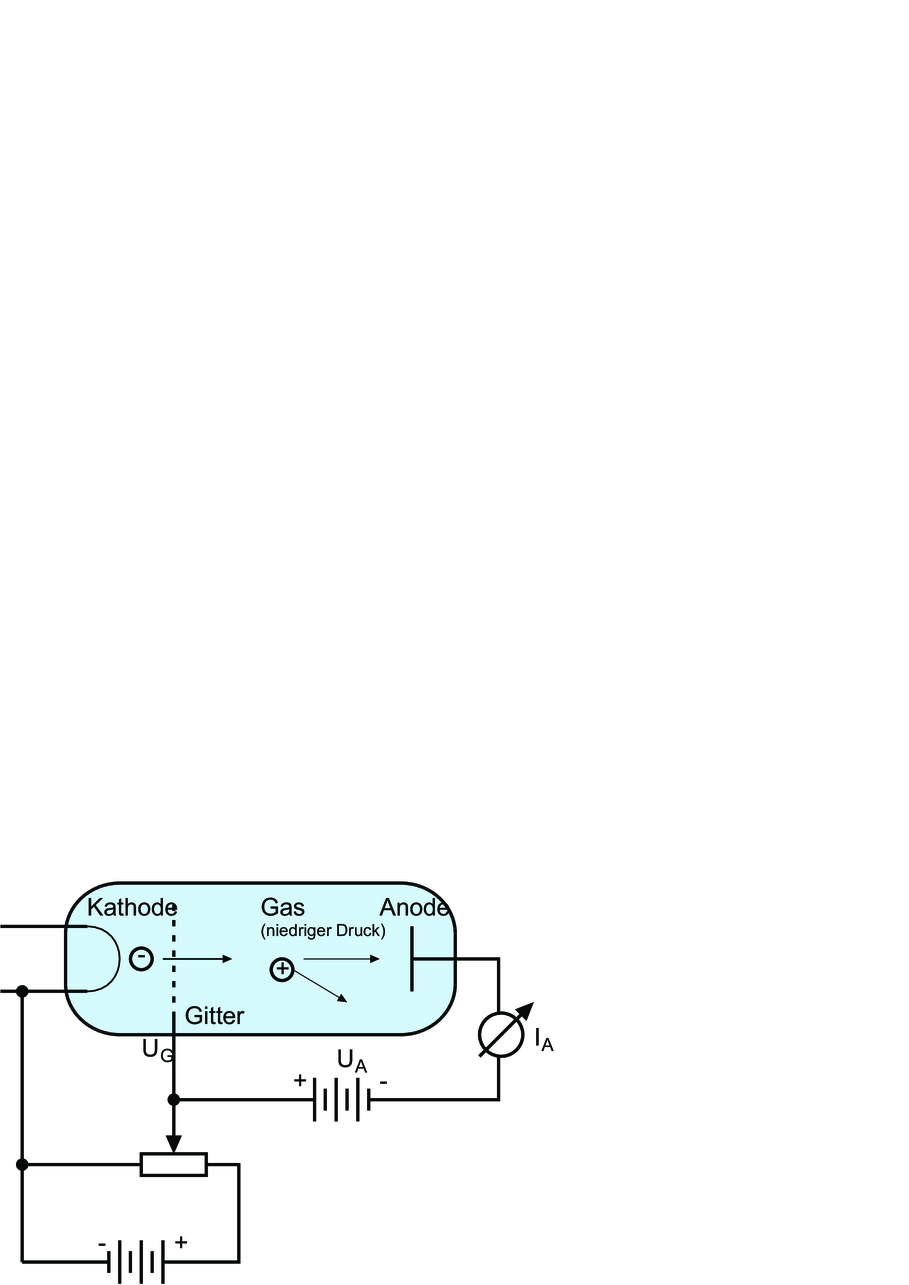
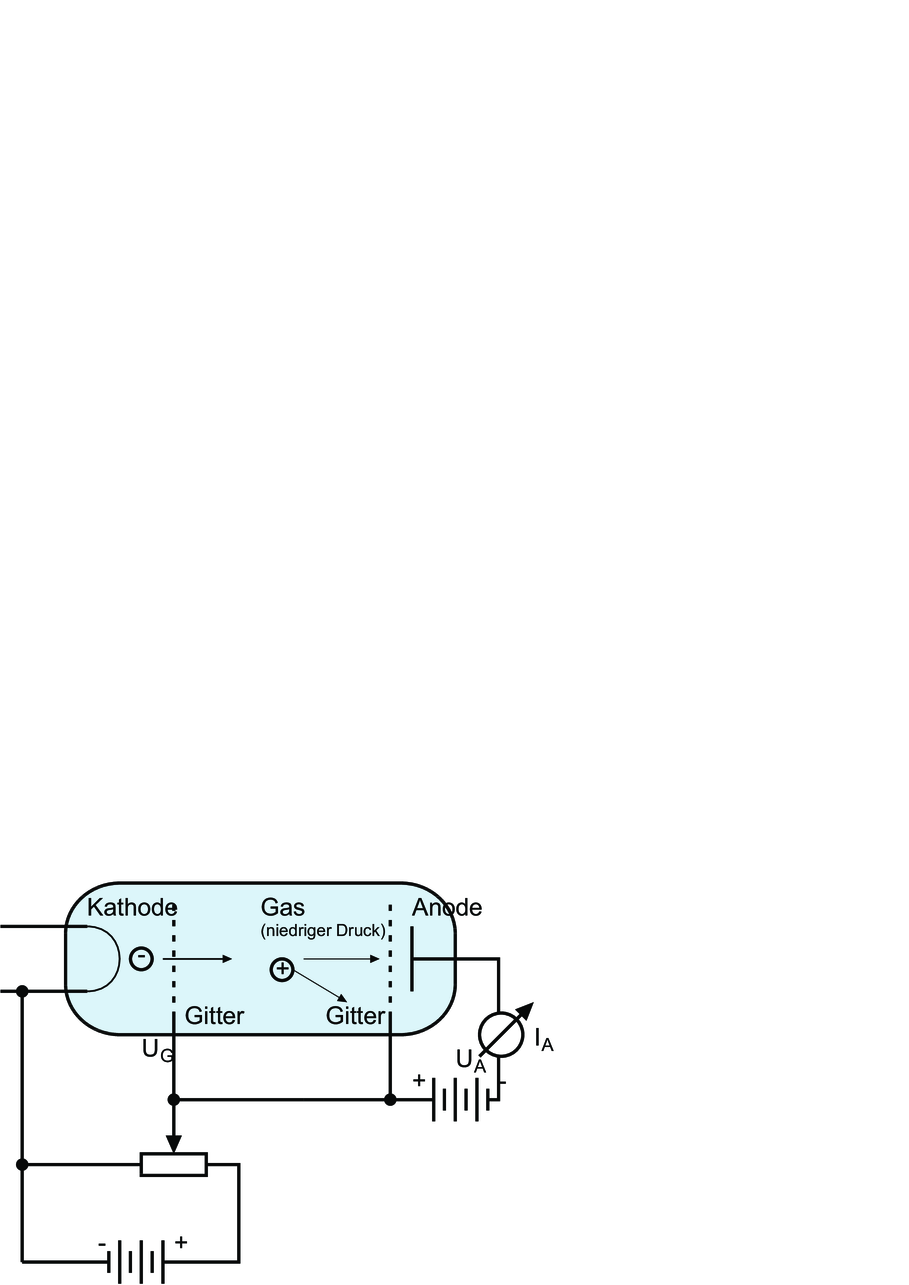
Abbildung 6.2 zeigt den Aufbau des Franck-Hertz-Versuches. Im Unterschied zum Lennard-Versuch ist die Anodenspannung gegen das Gitter geschaltet. Mit dieser negativen Spannung kann der Elektronenstrom als Funktion der Bremsspannung gemessen werden.
__________________________________________________________________________

Energieverhältnisse beim Franck-Hertz-Versuch. Die negative Anodenspannung UA hält niederenergetische Elektronen von der Anode fern.
_____________________________________________________________________
_____________________________________________________________________
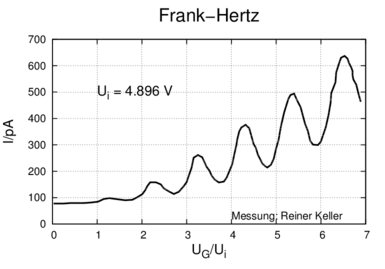
Resultat des Franck-Hertz-Versuches mit Quecksilber.
_____________________________________________________________________
Abbildung 6.2 zeigt die Potentialverhältnisse. Abbildung 6.2 zeigt eine Messung Herrn Reiner Kellers mit dem Vorlesungsversuch. Die Minima (oder Maxima) sind eUi = 4.88 eV = hc∕253.7 nm entfernt. Dies ist die Ionisierungsenergie von Hg. Immer wenn die kinetische Energie der Elektronen die Ionisierungsenergie überschreitet, können die Elektronen durch Stösse die Atome im Gas ionisieren. Die kinetische Energie der Elektronen sinkt um den Betrag der Ionisierungsenergie. Werden die Elektronen weiter beschleunigt, kann ihre Energie ein weiteres Mal die Ionisierungsenergie überschreiten. Durch Stösse verlieren die Elektronen kinetische Energie. Dieser bei genügender Beschleunigungsspannung mehrmals auftretende Effekt führt zu der in der Abbildung 6.2 gezeigten Kurvenform.
__________________________________________________________________________
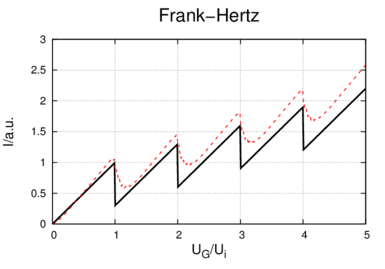
Resultat des Franck-Hertz-Versuches. Die schwarze Linie zeigt den Strom, den man mit einer Absorptionslinie und einer wohldefinierten Elektronenenergie erhalten würde. Die rote gestrichelte Linie berücksichtigt den Effekt der verschmierten Elektronenenergie.
_____________________________________________________________________
Die theoretisch erwartete Kurvenform ist in Abbildung 6.2 als Sägezahnkurve schwarz gezeichnet. Die Kurve wäre korrekt, wenn die Elektronen für eine bestimmte Beschleunigungsspannung nur eine scharf definierte kinetische Energie hätten.
__________________________________________________________________________
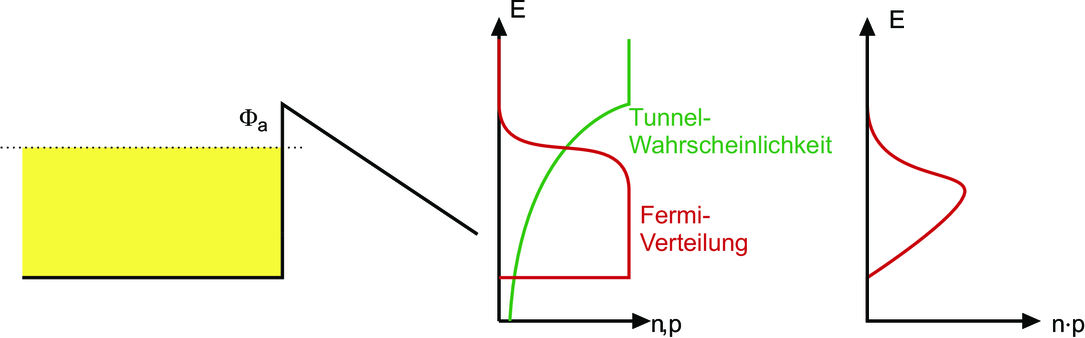
Die Elektronenverteilung bei der Emission ist durch das Produkt der Fermi-Verteilung und der Tunnelwahrscheinlichkeit gegeben.
_____________________________________________________________________
Wie Abbildung 6.2 zeigt, ist die kinetische Energie der aus einem Metall austretenden Elektronen über einen Energiebereich von 100 meV bis etwa 300 meV verteilt. Diese Verschmierung macht in Abbildung 6.2 aus der schwarzen Kurve die rote gestrichelte Kurve.
Die erneute Beschleunigung der Elektronen nach einem Stoss bewirkt eine Verzerrung der Kurvenform. Es wäre besser, wenn die Stösse im feldfreien Raume vonstatten gingen.
__________________________________________________________________________
_____________________________________________________________________
Abbildung 6.2 zeigt eine bessere Anordnung. Die beiden Gitter auf gleichem Potential erzeugen den benötigten feldfreien Raum. Bei dieser Anordnung ist es möglich, wie in der Skizze in Abbildung 6.2 gezeigt, mehrere Energieniveaus zu detektieren. Grössere Spannungen bedeuten dabei einen grösseren energetischen Abstand des Niveaus zum Vakuumniveau.
__________________________________________________________________________
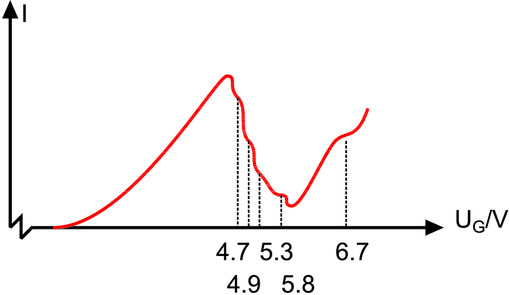
Ergebnis der genaueren Messung (Skizze)
_____________________________________________________________________
Arnold Sommerfeld wollte mit einer Erweiterung seiner Theorie im Jahre 1915 die Drehimpuls- und damit die Magnetfeldabhängigkeit der Spektrallinien erklären [Som16a, Som16b]. Sommerfeld nahm an, dass die Bahnen Ellipsen seien. Dies führt auf weitere Quantenzahlen, die sogenannten Nebenquantenzahlen. Eine elliptische Bahn kann als eine Bahn mit zwei Freiheitsgraden aufgefasst werden. Diese müssen durch zwei Quantenzahlen beschrieben werden, wobei die erste durch die Bohrsche Bedingung und die zweite durch
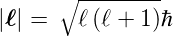 | (6.1) |
gegeben ist. Wenn in Gleichung (6.1) ℓ = 0 gesetzt
wird, sollte das Bohrsche Resultat entstehen. ℓ ist die
Bahndrehimpulsquantenzahl, 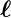 ist der Bahndrehimpuls. Die
Einheit des Bahndrehimpulses ist
ist der Bahndrehimpuls. Die
Einheit des Bahndrehimpulses ist ![[ℓ ]](ap-2015586x.png) =
= ![[ℏ]](ap-2015587x.png) = m·(ms−1)·kg = Js.
= m·(ms−1)·kg = Js.
Auch wenn wir heute wissen, dass Elektronen sich nicht auf einer Planetenbahn bewegen, ist es doch instruktiv, die Geschwindigkeit auszurechnen. Nach Gleichung (6.10) ist die kinetische Energie einer Bahn mit dem Radius r betragsmässig gleich der Gesamtenergie
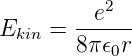
Für eine Bahn mit einem Radius von 0.5 nm ist die kinetische Energie
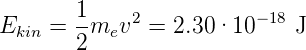
und damit die Geschwindigkeit
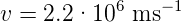
Die Geschwindigkeit ist im Prozentbereich der Lichtgeschwindigkeit, die relativistische Massenzunahme ist 2.82·10−5. Wenn nun relativistische Teilchen sich auf einer Ellipsenbahn bewegen, ist die Massenzunahme zeitabhängig. Die Bahnen sind nur noch angenähert Ellipsenbahnen, ihr Perihel dreht sich. Aus den Sommerfeldschen Berechnungen (klassisch mit Quantenbedingungen) folgte die Sommerfeldsche Feinstrukturkonstante:
Dabei ist verwendet worden, dass die erste Sommerfeldsche Bahn ℓ = 0 hat und damit nach Bohr eine Kreisbahn ist, bei der die Geschwindigkeit v konstant ist.
Nach Sommerfeld sind die Korrekturen der beobachteten Energieniveaus
![[ ]
Z2 α2Z2 ( n 3)
En,k = − RHhc --2 1 + ----- -----− -- + ...
n n ℓ + 1 4](ap-2015592x.png) | (6.3) |
Die Korrektur ist von der Grössenordnung 10−5, also spektroskopisch sehr gut messbar. Bei sehr hohen Energien kommt das Korrespondenzprinzip zum Tragen, dass jede nicht-klassische Theorie im Grenzfall hoher Energien und kleiner Energie-Änderungen in die klassische Theorie übergehen muss. Eine solche Realisation sind Rydberg-Atome.
 Lizenzinformationen
Lizenzinformationen