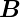 (
(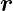 (t),t) und dem elektrischen Feld
(t),t) und dem elektrischen Feld
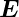 (
(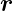 (t),t) mit
(t),t) mit 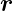 (t) =
(t) = 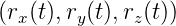 T lautet
T lautet

Die folgenden Ausführungen in diesem Abschnitt folgen [Fri10].
Die klassische Bewegungsgleichung eines Teilchens in der
magnetischen Induktion 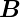 (
(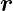 (t),t) und dem elektrischen Feld
(t),t) und dem elektrischen Feld
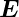 (
(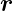 (t),t) mit
(t),t) mit 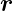 (t) =
(t) = 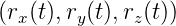 T lautet
T lautet
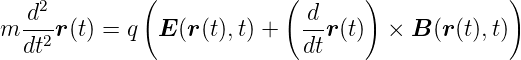 | (E.1) |
Die Felder können durch Potentiale ausgedrückt werden
Mit einer beliebigen Funktion Q(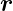 (t),t) können die
Potentiale modifiziert werden, ohne dass die Felder
(t),t) können die
Potentiale modifiziert werden, ohne dass die Felder  und
und 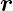 sich ändern.
sich ändern.
Gleichung (E.1) kann damit auch umgeschrieben werden
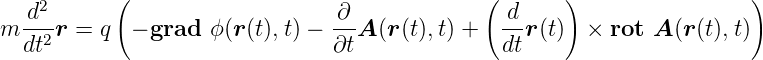 | (E.6) |
Die Behauptung ist nun, dass
auf die Gleichung (E.6) führt. Gezeigt wird dies durch Einsetzen in die kanonischen Gleichungen
Aus (E.8a) und (E.8b) folgt (die Angabe der Variablen, von denen die Funktionen abhängen, ist weggelassen.)
Aus Gleichung (E.9a) kann die Newtonsche Bewegungsgleichung geschrieben und mit (E.9b) ergänzt werden
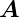 (
(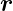 (t),t) hängt sowohl explizit wie implizit über
(t),t) hängt sowohl explizit wie implizit über 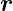 (t) von
der Zeit ab:
(t) von
der Zeit ab:
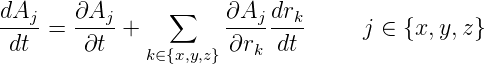 | (E.11) |
Gleichung (E.10) mit (E.11) und (E.9a) führt zu
Dies ist gerade die j-te Komponente von (E.6).
 Lizenzinformationen
Lizenzinformationen