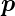 el =
el = 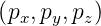 = e(x,y,z).
Zwischen zwei Wellenfunktionen ist das Dipolübergangsmatrixelement
für die Komponente des Dipolmoments px = e·x in die
x-Richtung definiert als
= e(x,y,z).
Zwischen zwei Wellenfunktionen ist das Dipolübergangsmatrixelement
für die Komponente des Dipolmoments px = e·x in die
x-Richtung definiert als

Wir betrachten ein Dipolmoment 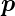 el =
el = 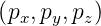 = e(x,y,z).
Zwischen zwei Wellenfunktionen ist das Dipolübergangsmatrixelement
für die Komponente des Dipolmoments px = e·x in die
x-Richtung definiert als
= e(x,y,z).
Zwischen zwei Wellenfunktionen ist das Dipolübergangsmatrixelement
für die Komponente des Dipolmoments px = e·x in die
x-Richtung definiert als
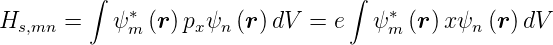 | (6.1) |
Ob ein bestimmtes Dipolübergangsmatrixelement Hs,mn
existiert, hängt von den Symmetrien der Wellenfunktion
ψn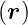 ab.
ab.
__________________________________________________________________________
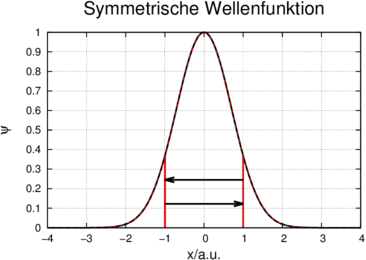
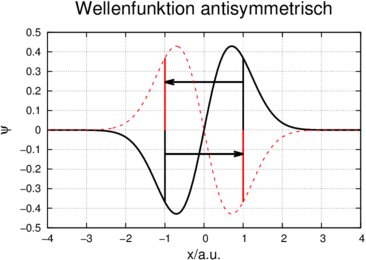
Links: Transformation x →−x für symmetrische und, rechts, für antisymmetrische Wellenfunktionen
_____________________________________________________________________
Abbildung 6.7 zeigt eine Skizze von symmetrischen und antisymmetrischen Wellenfunktionen. Wie die Abbildung zeigt, geht eine symmetrische Wellenfunktion bei der Transformation x →−x in sich selber über, während eine antisymmetrische Funktion am Nullpunkt punktgespiegelt wird. Im Folgenden nutzen wir die Symmetrie der Wellenfunktionen aus, um die erlaubten Übergänge zu bestimmen.
Beim harmonischen Oszillator ist die potentielle Energie proportional zu x2. Dann führt die Transformation x →−x
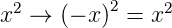 | (6.2) |
in sich selber über. Das heisst, das Potential des harmonischen Oszillators ist unverändert bei der Transformation x →−x. Dann gilt für das Potential
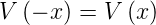 | (6.3) |
Ebenso ist die 2. Ableitung nach x für jede Funktion invariant unter der Transformation x →−x.
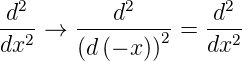 | (6.4) |
Wir betrachten nun die zeitunabhängige Schrödingergleichung
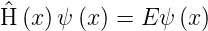 | (6.5) |
und transformieren sie mit x →−x
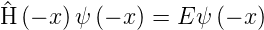 | (6.6) |
beim harmonischen Oszillator ist nun aber
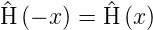 | (6.7) |
und damit auch
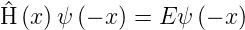 | (6.8) |
Das heisst, wenn ψ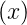 eine Eigenfunktion von
eine Eigenfunktion von 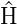
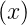 ist, ist
auch ψ
ist, ist
auch ψ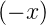 eine Eigenfunktion. Dabei haben wir implizit,
also ohne es ausdrücklich zu erwähnen, angenommen, dass es
zur Energie E nur eine Eigenfunktion (keine Entartung) gibt.
Deshalb muss gelten
eine Eigenfunktion. Dabei haben wir implizit,
also ohne es ausdrücklich zu erwähnen, angenommen, dass es
zur Energie E nur eine Eigenfunktion (keine Entartung) gibt.
Deshalb muss gelten
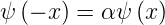 | (6.9) |
mit α einer komplexen Konstanten. Wir können aber
x auch durch −x ersetzen, da der Hamiltonoperator
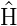 diese Symmetrie auch hat. Dann lautet Gleichung
(6.9)
diese Symmetrie auch hat. Dann lautet Gleichung
(6.9)
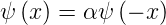 | (6.10) |
Wenn wir Gleichung (6.10) in Gleichung (6.9) einsetzen, dann gilt auch
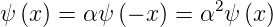 | (6.11) |
Wenn ψ(x) nicht identisch verschwindet, muss
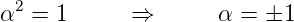 | (6.12) |
sein. Daraus folgt für die Wellenfunktion
 | (6.13) |
In drei Dimensionen ist die zur Transformation x →−x
äquivalente Transformation die Punktspiegelung am
Ursprung. Wir ersetzen in den obigen Betrachtungen x →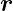 und erhalten die Transformation
und erhalten die Transformation
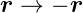 | (6.14) |
Ist nun 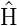
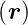 invariant gegen die Transformation
invariant gegen die Transformation 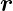 →−
→−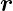 folgt für die Wellenfunktionen
folgt für die Wellenfunktionen
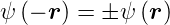 | (6.15) |
Die Transformation 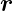 →−
→−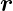 ist als Paritätstransformation
bekannt. Es gibt die beiden Fälle
ist als Paritätstransformation
bekannt. Es gibt die beiden Fälle
Die Parität von Wellenfunktionen ist in der Teilchenphysik von überragender Bedeutung. Ein mit dem Nobelpreis gewürdigtes Experiment von Chien-Shiung Wu (* 31. Mai 1912 in Shanghai, China; † 16. Februar 1997 in New York, USA) aus dem Jahre 1957 erbrachte den Nachweis, dass bei der schwachen Wechselwirkung die Paritätstransformation nicht gültig war. Man sagt: die Parität sei verletzt.
Beim harmonischen Oszillator gibt es Wellenfunktionen mit gerader und ungerader Parität, je nach der Hauptquantenzahl n:
Wir betrachten nun einen Hamiltonoperator 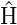 , der
mindestens Zylindersymmetrie oder aber eine höhere
Symmetrie haben soll. Mathematisch ausgedrückt bedeutet
die Zylindersymmetrie, dass
, der
mindestens Zylindersymmetrie oder aber eine höhere
Symmetrie haben soll. Mathematisch ausgedrückt bedeutet
die Zylindersymmetrie, dass
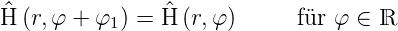 | (6.16) |
Bei einem sphärisch symmetrischen Hamiltonoperator
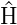 wie beim Coulombpotential sei 𝜗 konstant. Die
Schrödingergleichung lautet dann
wie beim Coulombpotential sei 𝜗 konstant. Die
Schrödingergleichung lautet dann
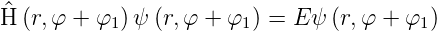 | (6.17) |
Wegen Gleichung (6.16) können wir auch schreiben
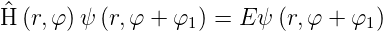 | (6.18) |
Da ψ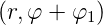 eine Eigenfunktion von
eine Eigenfunktion von 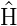
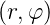 ist, gilt
auch
ist, gilt
auch
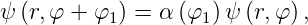 | (6.19) |
wobei α(φ1) eine komplexwertige Funktion des Winkels φ ist. Wenn wir eine Rotation um einen zweiten Winkel φ2 betrachten, gilt
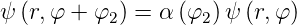 | (6.20) |
und damit auch
Andererseits folgt aus
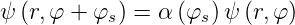 | (6.22) |
und
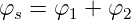 | (6.23) |
die Beziehung
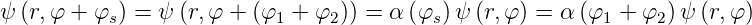 | (6.24) |
Aus den Gleichungen (6.21a) und (6.24)
folgt daraus die Beziehung
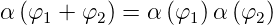 | (6.25) |
Die Mathematik sagt uns, dass die einzige mögliche Funktion mit diesen Eigenschaften
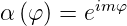 | (6.26) |
ist, wobei m noch unbekannt ist. Bei einer Drehung um φ = 2π erhalten wir wieder eine von der Ausgangslage ununterscheidbare Situation. Deshalb muss gelten
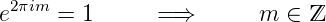 | (6.27) |
Dies ist nur möglich, wenn m eine ganze Zahl ist. Deshalb gilt auch
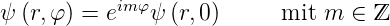 | (6.28) |
Unsere gefundene Zahl m ist kompatibel mit der magnetischen Quantenzahl m im Wasserstoffatom.
Das Übergangsmatrixelement für Dipolübergänge aus Gleichung (6.1) lautet entlang der x-Achse
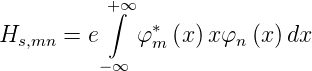 | (6.29) |
Deshalb definieren wir das Integral e·Imm = Hs,mm für die Matrixelemente auf der Hauptdiagonale
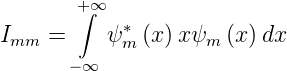 | (6.30) |
Bei der Transformation x →−x ergibt sich
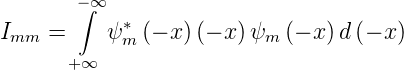 | (6.31) |
Wenn wir d(−x) durch dx ersetzen, müssen wir das Vorzeichen des Integrals wechseln
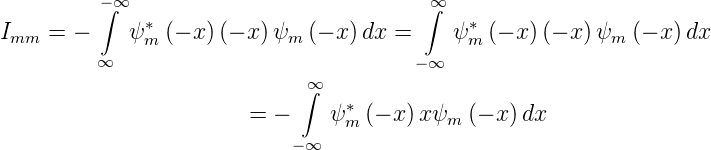 | (6.32) |
Bei der Transformation x → −x ändert ψ∗ mψm als quadratische Funktion das Vorzeichen nicht. Also folgt
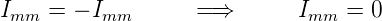 | (6.33) |
Das bedeutet, dass das Matrixelement Hs,mm ≡ 0 ist für alle m. Die Argumentation gilt auch für y und z. Es gibt in dieser Betrachtung keine Übergänge zwischen Zuständen mit der Quantenzahl m für Wellenfunktionen nach Abbildung 6.7.
Wenn m ⇔ n ist, lauten die Matrixelemente
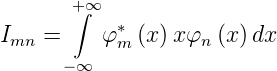 | (6.34) |
Falls nun φn und φm gleiche Parität haben ist Imn = 0. Das heisst, dass es für Wellenfunktionen nach Abbildung 6.7 keine Dipolübergänge geben kann bei denen Δm = m2 − m1 eine gerade Zahl ist. Bei ungleicher Parität der Wellenfunktionen ist Imn ⇔ 0. Diese Übergänge mit Δm = m2 −m1 = ±1,±3,… sind für Wellenfunktionen nach Abbildung 6.7 erlaubt.
Die Dipol-Matrixelemente des Wasserstoffatoms in die z-Richtung sind
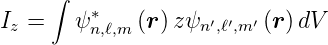 | (6.35) |
In Polarkoordinaten lauten sie
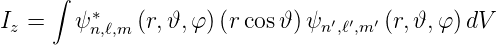 | (6.36) |
Wir betrachten Drehungen um die z-Achse um den Winkel
φ0. Wir verwenden die Transformationseigenschaft nach
Gleichung (6.28) und wenden sie auf Gleichung (6.36) an und
erhalten mit ψn,ℓ,m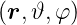
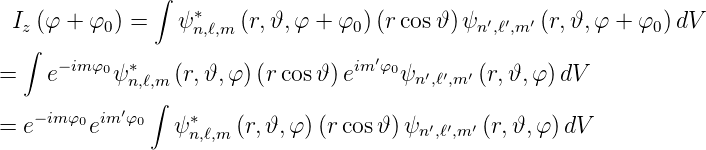 | (6.37) |
Damit ist
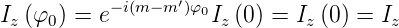 | (6.38) |
da dies eine Symmetrietransformation sein soll. Diese Gleichung hat zwei mögliche Lösungen. Entweder ist
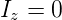 | (6.39) |
oder
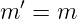 | (6.40) |
Für Übergänge, die das Dipolmoment des Wasserstoffs in die z-Richtung ansprechen, muss also m = m′ sein. Für die Dipolmomente in die x- und y-Richtung erhalten wir die reduzierten Integrale
Aus der Mathematik der komplexen Zahlen wissen wir, dass
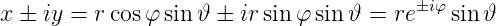 | (6.44) |
Damit können wir Gleichung (6.43) umschreiben
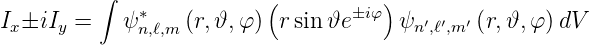 | (6.45) |
Wir drehen das Wasserstoffatom um φ0 um die z-Achse und erhalten
Mit Gleichung (6.46) lautet Gleichung (6.45) neu (der Faktor e±iφ fällt heraus)
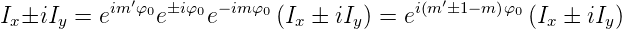 | (6.47) |
Damit Gleichung (6.47) erfüllt ist, muss gelten
Wenn eine komplexe Zahl null ist, sind Imaginär- und Realteil jeder für sich null.
Wir können also für das Wasserstoffatom die folgenden Regeln formulieren:
 Lizenzinformationen
Lizenzinformationen