Weiter: Elektrische Eigenschaften der Materie Oben: Elektrostatik Zurück: Kapazität: eine geometrische Eigenschaft Skript: PDF-Datei Übungen: Blätter
(Siehe Kneubühl, Repetitorium der Physik [Kne78, pp. 204]) (Siehe Tipler, Physik [TM04, pp. 729])
|
|
Ein Plattenkondensator der Kapazität ![]() sei auf die Spannung
sei auf die Spannung
![]() aufgeladen. Wir transportieren die
Ladung
aufgeladen. Wir transportieren die
Ladung ![]() von einer Seite zur anderen. Die Arbeit ist
von einer Seite zur anderen. Die Arbeit ist
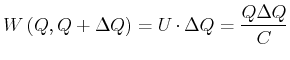 |
(2.91) |
Dabei haben wir die Ladung ![]() über die Potentialdifferenz
über die Potentialdifferenz ![]() transportiert.
transportiert.
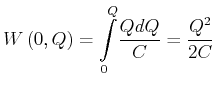 |
(2.92) |
also
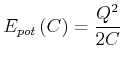 |
(2.93) |
oder mit
![]()
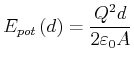 |
(2.94) |
oder mit
![]()
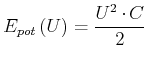 |
(2.95) |
Das Integral über die Oberfläche eines Leiters verknüpft die Ladung
![]() mit dem
elektrischen Feld. Das Volumen ist
mit dem
elektrischen Feld. Das Volumen ist
![]() . Zusammen ergibt sich
. Zusammen ergibt sich
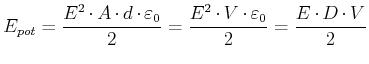 |
(2.96) |
oder mit
![]() der Energiedichte des elektrischen
Feldes
der Energiedichte des elektrischen
Feldes
Die Kraft
![]() auf ein Volumenelement
auf ein Volumenelement ![]() wird durch
wird durch
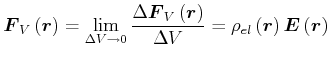 |
(2.98) |
beschrieben, da
| (2.99) |
Das elektrische Feld übt eine mechanische Spannung aus
Diese Spannung wird Maxwellspannung genannt. Sie hat die Einheit des Druckes. ![]() ist der
Normalenvektor der Oberfläche.
ist der
Normalenvektor der Oberfläche.
Die Oberflächenladungsdichte eines Metalls sei die Ursache des elektrischen Feldes. Wir hatten die
potentielle Energie im Feld des Plattenkondensators ausgerechnet:
![]() . Die Arbeit, den
Kondensator von
. Die Arbeit, den
Kondensator von ![]() auf
auf
![]() zu bringen ist.
zu bringen ist.
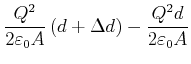 |
|||
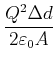 |
|||
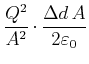 |
|||
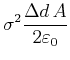 |
|||
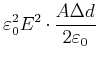 |
|||
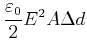 |
(2.101) |
und damit
Beispiel: In einem Laser können Felder von
![]() auftreten. Dies entspricht einer Maxwell-Spannung von
auftreten. Dies entspricht einer Maxwell-Spannung von
![]() bar.
bar.
| Wichtig: Energiedichten haben die Einheit des Druckes. In jedem Raumgebiet, in dem Energie gespeichert wird, herrscht Druck. |
|
|
Im Versuch Flächenladungsdichte
wird die Flächenladungsdichte gemessen, indem eine kleine Kugel in Kontakt mit verschieden grossen Kugeln auf einem konstanten Potential
![]() gebracht werden.
gebracht werden.
![\includegraphics[width=0.5\textwidth]{elektrostatik-035}](img385.gif)
|
In der Abbildung 2.28 wird der Messprozess schematisch gezeigt. Eine Kugel mit dem Radius ![]() wird auf die Spannung
wird auf die Spannung ![]() aufgeladen. Die kleine Kugel mit dem Radius
aufgeladen. Die kleine Kugel mit dem Radius ![]() wird mit der grossen Kugel in Kontakt gebracht. Nach kurzer Zeit haben beide Kugeln gegen Erde (unendlich) das Potential
wird mit der grossen Kugel in Kontakt gebracht. Nach kurzer Zeit haben beide Kugeln gegen Erde (unendlich) das Potential
![]() . Wenn wir annehmen, dass die kleine Kugel eine unwesentliche Störung der grossen Kugel ist, ist die Kapazität der beiden Kugeln
. Wenn wir annehmen, dass die kleine Kugel eine unwesentliche Störung der grossen Kugel ist, ist die Kapazität der beiden Kugeln
Die Flächenladungsdichte der beiden Kugeln im Kontakt ist durch
Die Kugel hat nach der Trennung ein anderes Potential gegen unendlich, nämlich
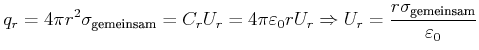
Aus Gleichung (2.105) und Gleichung (2.106) erhalten wir
Die Kugel wird schliesslich auf das Ladungsmessgerät (eigentlich ein Strom-Integrierer) aufgebracht. Die gemessene Ladung ist proportional zu ![]() und damit proportional zu
und damit proportional zu
![]() gemeinsam.
gemeinsam.
Othmar Marti