 Materialien
MaterialienFolien zur Vorlesung vom 30. 04. 2009: PDF
Aufgabenblatt 03 für das Seminar vom 06. 05. 2009 (Ausgabedatum 30. 04. 2009): (HTML oder PDF)

 Materialien
Materialien
Folien zur Vorlesung vom 30. 04. 2009: PDF
Aufgabenblatt 03 für das Seminar vom 06. 05. 2009 (Ausgabedatum 30. 04. 2009):
(HTML oder PDF)
(Siehe Kneubühl, Repetitorium der Physik [Kne78, pp. 192]) (Siehe Tipler, Physik [TM04, pp. 681])
Die Arbeit ist durch
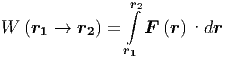 | (2.1) |
definiert.
Die potentielle Energie eines Kraftfeldes 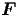
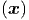 ist die Arbeit gegen diese Feldkraft.
Nach dem 3. Newtonschen Axiom ist
ist die Arbeit gegen diese Feldkraft.
Nach dem 3. Newtonschen Axiom ist 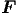 ext = -
ext = -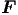 . Also
. Also
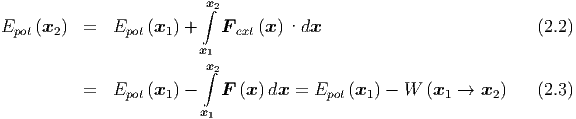
Eine potentielle Energie existiert, wenn
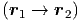 unabhängig vom Weg ist.
unabhängig vom Weg ist.
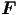
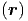 = 0 für alle
= 0 für alle 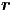
Die potentielle Energie einer Probeladung q im Feld der Ladung Q ist
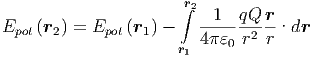 | (2.4) |
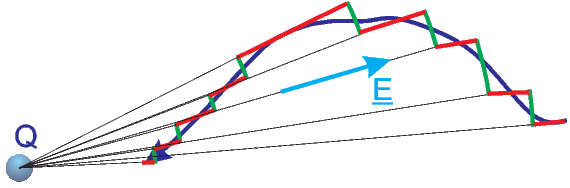
Approximation eines beliebigen Integrationsweges durch Kreissegmente.
Auf den Kreissegmenten (grün) ist ∫
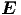 ·d
·d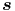 = 0, entlang der radialen
Teile ist ∫
= 0, entlang der radialen
Teile ist ∫
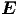 ·d
·d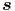 = ∫
E(r)ds.
= ∫
E(r)ds.
Da wir jede Bahnkurve durch Stücke in radialer Richtung und durch Bahnen mit
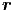 = const approximieren können, und da die Bahnen auf den Kugelflächen keinen
Beitrag geben (sie sind senkrecht zur Kraft) können wir das Integral vereinfachen.
= const approximieren können, und da die Bahnen auf den Kugelflächen keinen
Beitrag geben (sie sind senkrecht zur Kraft) können wir das Integral vereinfachen.
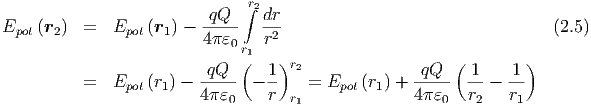
Üblicherweise setzt man Epot = 0. Damit wird
= 0. Damit wird
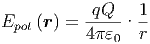 | (2.6) |
Aus der potentiellen Energie kann die Kraft mit dem Gradienten
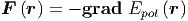 | (2.7) |
berechnet werden. Für die potentielle Energie der Coulomb-Kraft bekommen wir
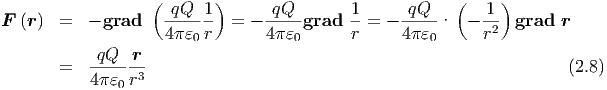
In Komponenten ist r = 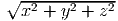 und grad =
und grad =  =
= 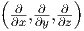
Also
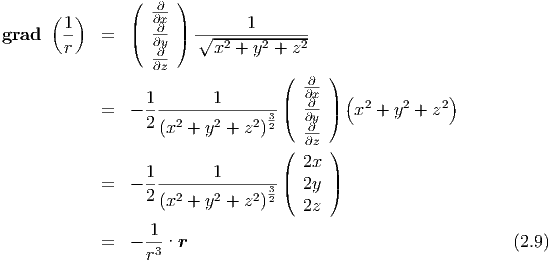
Ergänzend zu Coulomb-Kraft hatten wir das elektrische Feld als auf eine Einheitsladung normierte Grösse eingeführt.
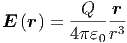 | (2.10) |
Die potentielle Energie der Ladung q im Feld der Ladung Q, normiert auf q = 1 ist das elektrische Potential φ, auch Spannung U genannt. Ich verwende in diesem Skript die Begriffe elektrisches Potential und Spannung austauschbar.
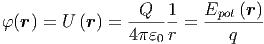 | (2.11) |
Wichtig ist die Beziehung
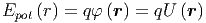 | (2.12) |
Wie die Kraft aus der potentiellen Energie über die Gradientenbildung hervorgeht, wird das elektrische Feld mit
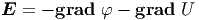 | (2.13) |
berechnet.
Folgende Relationen gelten
Wir merken uns
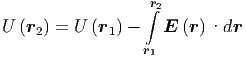 | (2.15) |
analog zur potentiellen Energie.
Die Einheit des elektrostatischen Potentials oder der Spannung ist
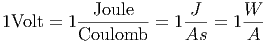
Bem.: Beim elektrischen Feld ist der Feldvektor  , bei der Gravitation
, bei der Gravitation 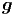
Das Gravitationspotential ist Ugrav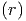 = -G
= -G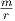 .
.
Da die Coulomb-Kräfte additiv sind, ist auch das elektrostatische Potential oder die
elektrostatische potentielle Energie additiv. Das Potential von Ladungen qi an den
Orten 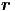 i ist also
i ist also
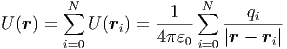 | (2.16) |
Für kontinuierliche Ladungsverteilungen ρel(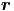 ) ist das Potential
) ist das Potential
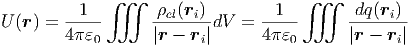 | (2.17) |
 Versuch zur Vorlesung: Flächenladungsdichte (Versuchskarte
ES-8)
Versuch zur Vorlesung: Flächenladungsdichte (Versuchskarte
ES-8)
Eine homogen mit der Flächenladungsdichte σ geladene Ebene erzeugt ein konstantes elektrisches Feld E = σ∕(2ε0). Das elektrostatische Potential eines Punktes P im Abstand x > 0 von der Platte kann gefunden werden, indem wir entlang des Lots vom Punkt P auf die Ebene integrieren.
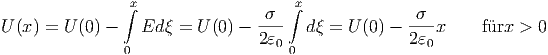 | (2.18) |
Für x < 0 berechnet man
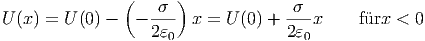 | (2.19) |
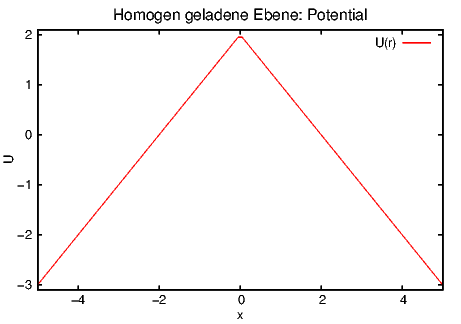
Potential senkrecht zu einer homogen geladenen Ebene mit U0 = 2 und σ = 2ε0.
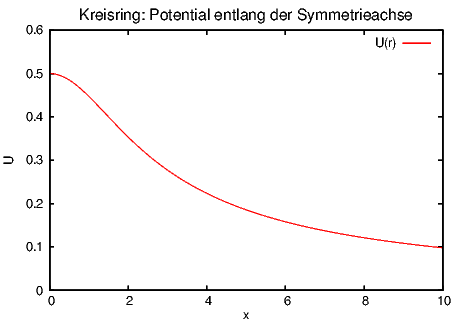
Das elektrostatische Potential eines Kreisringes mit der Ladung Q und dem Radius R im Abstand x auf der Symmetrieachse soll berechnet werden. Wir verwenden, dass
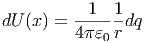
ist, mit
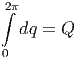
Wir erhalten
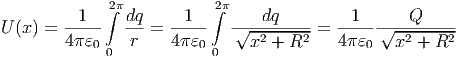 | (2.20) |
Analog kann das Potential einer homogen geladenen Scheibe mit dem Radius R entlang ihrer Symmetrieachse x berechnet werden. Die Ladungsdichte der Scheibe sei σ = Q∕(πR2). Ein Kreisring mit dem Radius a trägt die Ladung dq = 2πaσda und erzeugt dann das Potential
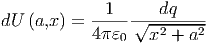 | (2.21) |
Durch Integration über die gesamte Scheibe erhalten wir
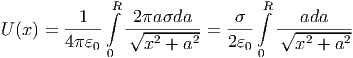 | (2.22) |
Dieses Integral ergibt nach Bronstein[BSMM00, Seite 309, Nr. 193]
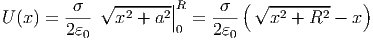 | (2.23) |
Asymptotisch verläuft auch dieses Potential für x →∞ wie das Potential einer Punktladung, da
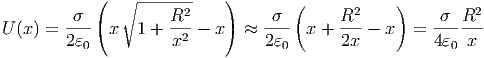
Für den anderen Grenzfall berechnen wir die Taylorreihe um 0 bis zum ersten Glied.
| U(0) | = 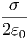 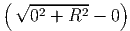 | ||||||
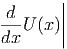 x=0 x=0 | = 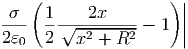 x=0 x=0 | = | -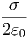 | ||||
| U(x) | ≈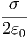 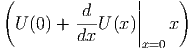 | = | 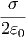 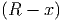 |
Die beiden Grenzfälle zeigen, dass sich die geladene Kreisplatte für x » R wie eine Punktladung und für x « R wie eine unendlich ausgedehnte Platte verhält.
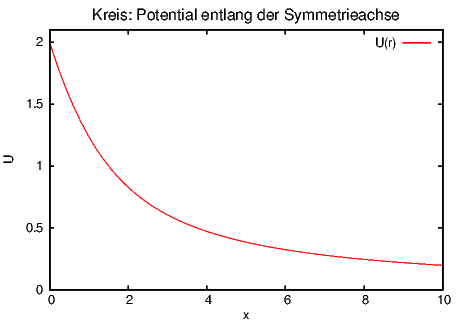
Elektrostatisches Potential einer homogen geladenen Kreisscheibe entlang ihrer Symmetrieachse mit R = 2 und σ = 2ε0.
Das Potential einer homogen geladenen Kugelschale wird mit dem elektrischen
Feld berechnet. Das radiale elektrische Feld ist Er(r) = 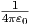
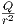 . Damit ist das
Potential
. Damit ist das
Potential
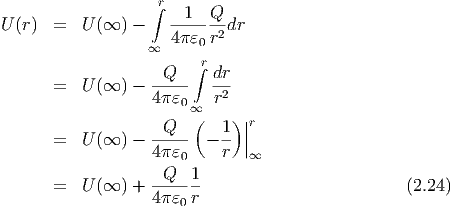
Oder mit U(∞) = 0
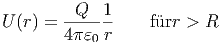 | (2.25) |
Innerhalb der Kugelschale ist das elektrische Feld null, das Potential also konstant.
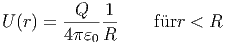 | (2.26) |
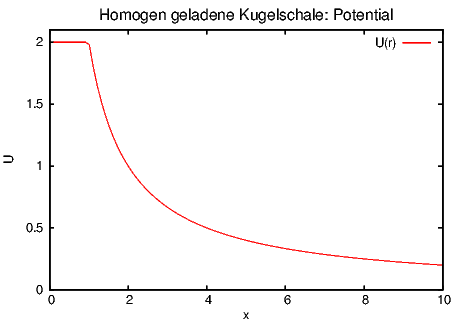
Potential einer homogen geladenen Kugelschale mit R = 1 und Q = 8πε0.
Schliesslich berechnen wir das elektrostatische Potential in der Nähe einer unendlich ausgedehnten Linienladung mit der Ladungsdichte λ. Das radiale elektrische Feld ist E = λ∕(2πε0x). Das Potential ist dann
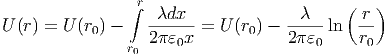 | (2.27) |
Wir setzen U(r0) = 0 und erhalten
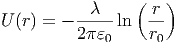 | (2.28) |
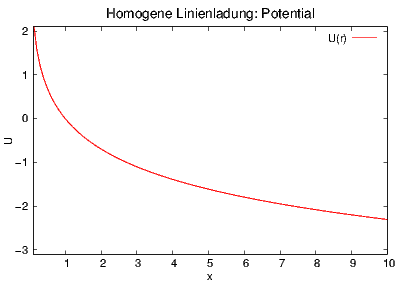
Potential in der Nähe einer unendlich ausgedehnten homogenen Linienladung mit r0 = 1 und λ = 2πε0.
 Lizenzinformationen
Lizenzinformationen