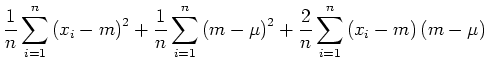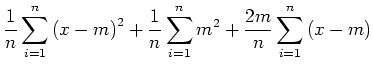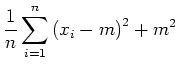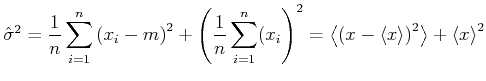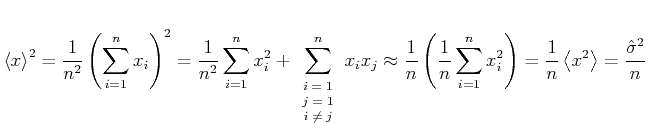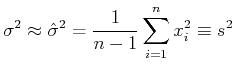Weiter: Mittlerer Fehler des Mittelwertes
Oben: Statistische Fehler
Zurück: Varianzen und Standardabweichungen
Da der Mittelwert der Grundgesamtheit, 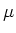 , im allgemeinen nicht bekannt ist, wird die berechnete Varianz nicht
die Varianz der Grundgesamtheit sein. Wir versuchen nun den besten Schätzwert für die Varianz zu berechnen. Nehmen
wir an, wir würden
, im allgemeinen nicht bekannt ist, wird die berechnete Varianz nicht
die Varianz der Grundgesamtheit sein. Wir versuchen nun den besten Schätzwert für die Varianz zu berechnen. Nehmen
wir an, wir würden 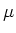 kennen. Dann gilt
kennen. Dann gilt
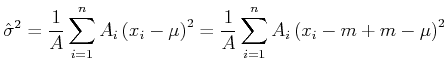 |
(3.17) |
wobei
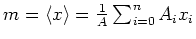 der Mittelwert der gemessenen
der Mittelwert der gemessenen 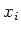 ist.
ist.
Im folgenden setzen wir alle 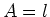 und
und 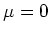 . Dann ist
. Dann ist 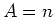 . Durch Ausmultiplizieren erhalten wir
. Durch Ausmultiplizieren erhalten wir
mit
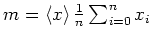 erhält man
erhält man
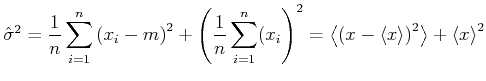 |
(3.19) |
Mit
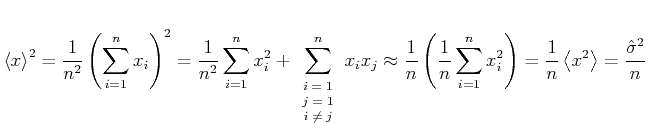 |
(3.20) |
wird
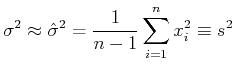 |
(3.21) |
Die Grösse 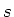 ist der mittlere Fehler einer Einzelmessung. Der Übergang von
ist der mittlere Fehler einer Einzelmessung. Der Übergang von 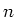 nach
nach 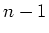 ist zu
Verstehen als der Verlust eines Freiheitsgrades. Da wir den Mittelwert der Grundgesamtheit
ist zu
Verstehen als der Verlust eines Freiheitsgrades. Da wir den Mittelwert der Grundgesamtheit 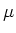 nicht kennen,
muss die Stichprobe zur Bestimmung von
nicht kennen,
muss die Stichprobe zur Bestimmung von 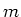 herhalten. Dies ergibt eine neue Beziehung zwischen den Datensätzen,
reduziert alsodie Anzahl Freiheitsgrade.
herhalten. Dies ergibt eine neue Beziehung zwischen den Datensätzen,
reduziert alsodie Anzahl Freiheitsgrade.





Next: Mittlerer Fehler des Mittelwertes
Up: Statistische Fehler
Previous: Varianzen und Standardabweichungen
Othmar Marti
Experimentelle Physik
Universiät Ulm
![]() , im allgemeinen nicht bekannt ist, wird die berechnete Varianz nicht
die Varianz der Grundgesamtheit sein. Wir versuchen nun den besten Schätzwert für die Varianz zu berechnen. Nehmen
wir an, wir würden
, im allgemeinen nicht bekannt ist, wird die berechnete Varianz nicht
die Varianz der Grundgesamtheit sein. Wir versuchen nun den besten Schätzwert für die Varianz zu berechnen. Nehmen
wir an, wir würden ![]() kennen. Dann gilt
kennen. Dann gilt
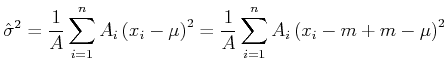
![]() und
und ![]() . Dann ist
. Dann ist ![]() . Durch Ausmultiplizieren erhalten wir
. Durch Ausmultiplizieren erhalten wir