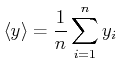 |
(3.22) |
Bei verschiedenen Stichproben schwanken der Mittelwert und die Varianz. Wenn wir für die Berechnung des Mittelwertes die Schreibweise
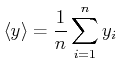 |
(3.22) |
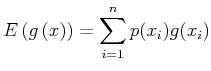 |
(3.23) |
![$\displaystyle E\left[\frac{1}{n} \sum\limits_{i=1}^n x_i -\mu\right]^2$](img77.gif) |
(3.24) | ||
![$\displaystyle E\left[\frac{1}{n} \sum\limits_{i=1}^n \left(x_i -\mu\right)\right]^2$](img78.gif) |
|||
![$\displaystyle \frac{1}{n^2} \sum\limits_{i=1}^n E\left[\left(x_i -\mu\right)^2\...
... \\
\end{array}}^n E\left[\left(x_i -\mu\right)\left(x_i -\mu\right)\right]
$](img79.gif) |
![$ \frac{1}{n^2}
\sum\limits_{\scriptsize\begin{array}{c}
i=1 \\
j=1 \\
i ...
...end{array}}^n E\left[\left(x_i -\mu\right)\left(x_i -\mu\right)\right]\approx 0$](img80.gif) und wir erhalten
und wir erhalten
![$\displaystyle \sigma_m^2 = \frac{1}{n^2} n E\left[\left( x_i -\mu\right)^2\right]=\frac{\sigma^2}{n}$](img81.gif) |
(3.25) |
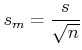 |
(3.26) |
| Daraus lernt man, dass, um ein Resultat doppelt so genau zu erhalten, viermal mehr Messungen durchgeführt werden müssen. |