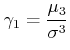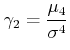Weiter: Robuste numerische Berechnung von Oben: Statistische Fehler Zurück: Mittlerer Fehler des Mittelwertes

Momente der Verteilung

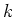Das $k$-te Moment einer Verteilung ist definiert durch den Erwartungswert

$$\mu_k(x,B) = E\left[\left(x-B\right)^k\right]$$ (3.27)

Wenn wir 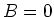$B=0$ setzen, so erhalten wir

$$\mu_1' = E(x) = \left< x \right> = \overline{x}$$ (3.28)

$$\mu_2' = \sigma^2(0) =\left< x^2 \right> = \overline{x^2}$$

Bei den höheren Momenten benutzt man eine Normierung, damit diese dimensionslos werden.

Gebräuchlich ausser dem Mittelwert und der Varianz sind:

• Die Schiefe (skewness):

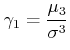  $$\gamma_1 = \frac{\mu_3}{\sigma^3}$$ (3.29)

  
  
  Wenn die Schiefe positiv ist, heisst das, dass grössere Abweichungen auf der positiven Seite liegen. Symmetrische Verteilungen haben die Schiefe $\gamma_1 =0$.
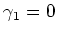• Die Überhöhung (peakedness):

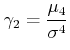  $$\gamma_2 = \frac{\mu_4}{\sigma^4}$$ (3.30)

  
  
  Die Grösse 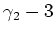$\gamma_2-3$ heisst Exzess, da sie die Abweichung von der Gaussverteilung angibt.