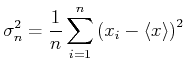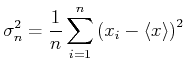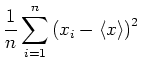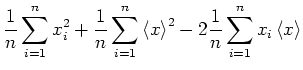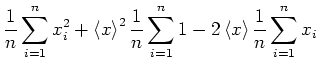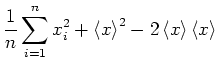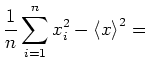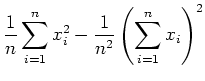Weiter: Rekursionsformel für Mittelwerte Oben: Vorlesungsskript Einführung in die Zurück: Momente der Verteilung

Robuste numerische Berechnung von Mittelwerten und Varianzen

Was ist zu tun bei der Berechnung der Varianz und der höheren Momente, wenn neue Messwerte hinzukommen?

• Man berechnet vom Mittelwert ausgehend jede Kenngrösse über alle Messwerte neu. Dies ist zeitaufwendig, und der Aufwand steigt, je grösser das betrachtete Ensemble ist.
• Man rechnet die relevanten Gleichungen so um, dass immer nur Summen der Messwerte, Summen der Quadrate der Messwerte, usw, nie aber wie bei der Varianz Summen von Quadraten von Differenzen zwischen Messwerten und Mittelwerten vorkommen. Im letzten Falle tritt numerische Auslöschung ein.
• Man verwendet Rekursionsformeln

Wir betrachten die Varianz für 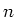$n$ Messwerte als Beispiel.

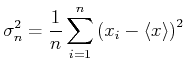$$\sigma_n^2=\frac{1}{n}\sum\limits_{i=1}^{n}\left(x_i-\left< x \right>\right)^2$$ (4.31)

Wir formen um

$$\sigma_n^2 = \frac{1}{n}\sum\limits_{i=1}^{n}\left(x_i-\left< x \right>\right)^2$$ (4.32)

$$ = \frac{1}{n}\sum\limits_{i=1}^{n}x_i^2+\frac{1}{n}\sum\limits_{i=1}^{n}\left< x\right>^2 -2\frac{1}{n}\sum\limits_{i=1}^{n}x_i\left<x\right>$$

$$ = \frac{1}{n}\sum\limits_{i=1}^{n}x_i^2+\left< x\right>^2\frac{1}{n}\sum\limits_{i=1}^{n}1 -2\left<x\right>\frac{1}{n}\sum\limits_{i=1}^{n}x_i$$

$$ = \frac{1}{n}\sum\limits_{i=1}^{n}x_i^2+\left< x\right>^2 -2\left<x\right>\left<x\right>$$

$$ = \frac{1}{n}\sum\limits_{i=1}^{n}x_i^2 -\left<x\right>^2 =$$

$$\sigma_n^2 = \frac{1}{n}\sum\limits_{i=1}^{n}x_i^2-\frac{1}{n^2}\left(\sum\limits_{i=1}^{n}x_i\right)^2$$

Bei dieser Formel kann, wenn ein Messwert hinzugefügt wird, einfach die beiden Summen erhöht und dann neu gerechnet werden. Das Problem ist, dass die Beiden Summanden sehr gross werden, dass also numerische Auslöschung eintritt.