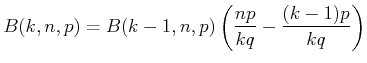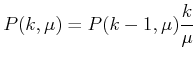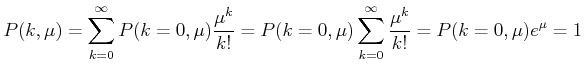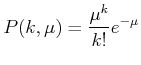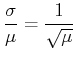Weiter: Lorentz-Verteilung
Oben: Verteilungen
Zurück: Normalverteilung
Bei radioaktiven Atomen ist die Anzahl in einer bestimmten Zeit zerfallender Kerne proportional zur Gesamtzahl der
Kerne. Es gilt also
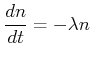 |
(5.62) |
Daraus folgt das Zerfallsgesetz
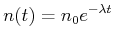 |
(5.63) |
Anstelle der Zerfallskonstante wird meistens die Halbwertszeit
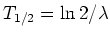 angegeben. Unter den
folgenden Annahmen kann man die dazugehörige Verteilungsfunktion ableiten.
angegeben. Unter den
folgenden Annahmen kann man die dazugehörige Verteilungsfunktion ableiten.
- Die Zahl der radioaktiven Kerne sei sehr hoch (Diese Forderung wird meistens sehr gut erfüllt).
- Die Anzahl der Zerfälle werde in jeweils konstanten Intervallen
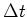 bestimmt.
bestimmt.
- Die Zerfallswahrscheinlichkeit
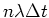 sei in jedem Messintervall gleich, was
gleichbedeutend ist mit
sei in jedem Messintervall gleich, was
gleichbedeutend ist mit
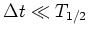 .
.
Viele Stösse ergeben nun eine Folge von Stosszeiten (
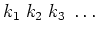 ). Wir berechnen nun den
Erwartungswert
). Wir berechnen nun den
Erwartungswert
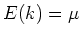 . Mit der Zerfallswahrscheinlichkeit
. Mit der Zerfallswahrscheinlichkeit 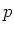 (proportional zu
(proportional zu 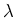 und
und 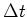 ) wird
) wird
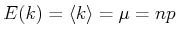 |
(5.64) |
Die Wahrscheinlichkeit für eine Zahl 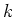 von Ereignissen im Messintervall
von Ereignissen im Messintervall 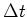 kann aus der
Binomialverteilung durch einen Grenzübergang nach unendlich (
kann aus der
Binomialverteilung durch einen Grenzübergang nach unendlich (
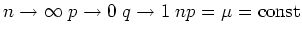 ) berechnet werden. Wir verwenden die Rekursionsformel für die Binomialverteilung
) berechnet werden. Wir verwenden die Rekursionsformel für die Binomialverteilung
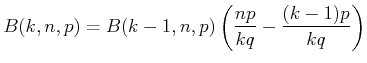 |
(5.65) |
Daraus entsteht die Rekursionsformel für die Poisson-Verteilung
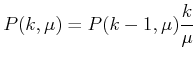 |
(5.66) |
Mit der Normierungsbedingung
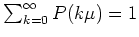 bekommt man
bekommt man
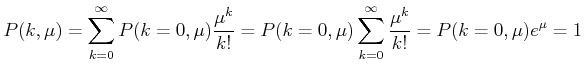 |
(5.67) |
Und daraus die Poisson-Verteilung
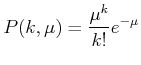 |
(5.68) |
Die Poisson-Verteilung hat die folgenden Eigenschaften (erhalten aus dem Vergleich mit der Binomialverteilung):
- Mittelwert
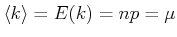 |
(5.69) |
- Varianz
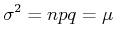 |
(5.70) |
(da 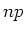 konstant ist und
konstant ist und 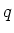 gegen
gegen 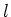 geht!)
geht!)
- Die Poisson-Verteilung ist normiert.
- Die Poisson-Verteilung hat nur einen Parameter, nämlich den Mittelwert
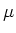
- Der relative mittlere Fehler ist
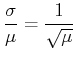 |
(5.71) |
Die Poisson-Verteilung findet man immer dann, wenn ein sehr unwahrscheinliches Ereignis bei einer grossen Zahl
Versuchen betrachtet wird. Neben Atomkernen sind auch die Ankunftszeiten von Photonen und Elektronen bei sehr
geringem Fluss Poisson-verteilt.





Next: Lorentz-Verteilung
Up: Verteilungen
Previous: Normalverteilung
Othmar Marti
Experimentelle Physik
Universiät Ulm
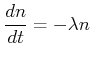
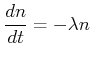
![]() ). Wir berechnen nun den
Erwartungswert
). Wir berechnen nun den
Erwartungswert
![]() . Mit der Zerfallswahrscheinlichkeit
. Mit der Zerfallswahrscheinlichkeit ![]() (proportional zu
(proportional zu ![]() und
und ![]() ) wird
) wird