Der t-Test gibt eine Angabe über die Konsistenz zweier Mittelwerte. Er erlaubt eine Aussage, ob eine eigene Messung mit der eines ändern (aber auch eine frühere eigene Messung) konsistent ist. Damit kann getestet werden, ob eine Apparatur sich mit der Zeit verändert.
Man könnte zur Annahme gelangen, dass wenn zwei Mittelwerte
![]() und
und
![]() sich um
weniger als eine Standardabweichung unterscheiden, dass sie dann zu einer identischen Grundgesamtheit gehören.
Diese Beurteilung ist willkürlich.
sich um
weniger als eine Standardabweichung unterscheiden, dass sie dann zu einer identischen Grundgesamtheit gehören.
Diese Beurteilung ist willkürlich.
Besser ist es, den erwarteten Fehler der Differenz
![]() zu berechnen. Mit Hilfe des Fehlerfortpflanzungsgesetzes (siehe auch Kapitel
7) ergibt sich
zu berechnen. Mit Hilfe des Fehlerfortpflanzungsgesetzes (siehe auch Kapitel
7) ergibt sich
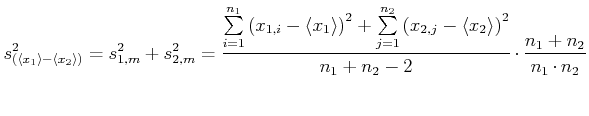 |
(6.77) |
dabei sind
![]() und
und
![]() die Mittelwerte zweier Messreihen,
die Mittelwerte zweier Messreihen, ![]() und
und ![]() die Anzahl Messungen mit den Fehlern
die Anzahl Messungen mit den Fehlern
![]() und
und ![]() . Für
. Für ![]() setzt man am besten
setzt man am besten
![]() ein, wobei die Varianz durch das Zusammenlegen aller Messreihen berechnet wurde. Ebenso ersetzt man
ein, wobei die Varianz durch das Zusammenlegen aller Messreihen berechnet wurde. Ebenso ersetzt man
![]() mit
mit
![]() .
.
Für die ![]() -Verteilung und den
-Verteilung und den ![]() -Test betrachtet man normalverteilte Zufallsvariablen
-Test betrachtet man normalverteilte Zufallsvariablen ![]() . Sind solche nicht
vorhanden, dann muss mit Mittelwerten von Stichproben gerechnet werden. Wir berechnen den Mittelwert
. Sind solche nicht
vorhanden, dann muss mit Mittelwerten von Stichproben gerechnet werden. Wir berechnen den Mittelwert ![]() aus
der Stichprobe
aus
der Stichprobe ![]() und die Standardabweichung
und die Standardabweichung ![]() , die auf
, die auf ![]() Freiheitsgeraden beruht. Die
Freiheitsgeraden beruht. Die ![]() -Grösse ist
dann
-Grösse ist
dann
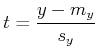 |
(6.78) |
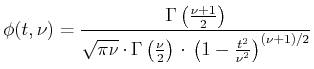 |
(6.79) |
| (6.80) | |||
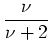 |
|||
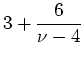 |
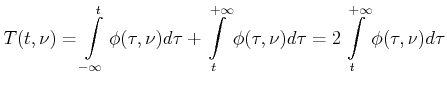 |
(6.81) |
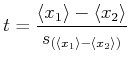 |
(6.82) |
Wenn der Test erfüllt ist, dann sind die beiden Stichproben aus der gleichen Grundgesamtheit.
Zwei Mittelwerte mit ![]() und
und ![]() ergeben einen
ergeben einen ![]() -Wert von
-Wert von ![]() . Es gibt insgesamt
. Es gibt insgesamt
![]() Freiheitsgrade. Man findet
Freiheitsgrade. Man findet
![]() (Die entsprechende
Excel-Funktion =TVERT(1,74;14;2) liefert den Wert
(Die entsprechende
Excel-Funktion =TVERT(1,74;14;2) liefert den Wert
![]() ) Die Interpretation sagt nun,
dass
) Die Interpretation sagt nun,
dass