Im allgemeinen besteht ein Resultat eines physikalischen Experimentes nicht aus einer einzelnen Messgrösse. Wir können also die oben abgeleiteten Verfahren nicht unbesehen auf beliebige experimentelle Resultate ausdehnen. Wie wirken sich also die Einzelfehler auf die Gesamtheit aus?
Als Beispiel soll die Bestimmung einer Gitterkonstanten ![]() nach der Debye-Scherrer-Methode besprochen werden.
Röntgenstrahlen mit der Wellenklänge
nach der Debye-Scherrer-Methode besprochen werden.
Röntgenstrahlen mit der Wellenklänge ![]() fallen auf eine grössere Anzahl kleiner Kristallite mit den
Miller'sehen Indizes
fallen auf eine grössere Anzahl kleiner Kristallite mit den
Miller'sehen Indizes ![]() . Für den Glanzwinkel gilt:
. Für den Glanzwinkel gilt:
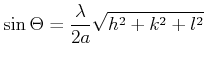 |
(7.89) |
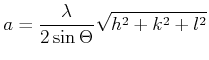 |
(7.90) |
(a), (b) und (c) sind systematische Fehler. Bei (b) und (c) lassen sich
Vorzeichen und Grösse des Fehlers bestimmen. Bei (a) ist der Fehler für unsere Messung ein systematischer,
beruht aber ursprünglich auf der Bestimmung eines zufälligen Fehlers, so dass
![]() zur Abschätzung des
systematischen Fehlers verwendet werden kann.
zur Abschätzung des
systematischen Fehlers verwendet werden kann.