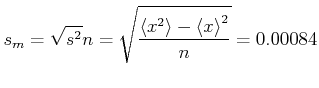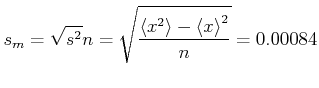Weiter: t-Test
Oben: Vorlesungsskript Einführung in die
Zurück: Lorentz-Verteilung
Die in physikalischen Experimenten erhaltenen Daten stellen Stichproben
aus einer Grundgesamtheit dar. Wir müssen nun die folgenden
Fragen lösen:
- Stammen zwei Messreihen (Stichproben) aus der gleichen, unbekannten Grundgesamtheit?
- Passt eine Messreihe zu früheren, ausgedehnten Stichproben (Hat die Probe sich verändert?)
- Passt eine Stichprobe zu einer Modellverteilung oder Hypothese?
Ein einfacher Test kann anhand der Standardabweichungen durchgeführt werden. So soll untersucht werden, ob bei
einer Gesamtwurfzahl von 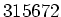 die Zahl von
die Zahl von 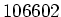 Würfen der Zahlen
Würfen der Zahlen 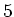 oder
oder 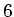 zur Annahme eines homogenen
Würfels (
zur Annahme eines homogenen
Würfels (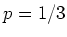 ) passt. Im Versuch ist die relative Häufigkeit
) passt. Im Versuch ist die relative Häufigkeit
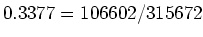 . Weiter ist die
Standardabweichung des Mittelwertes
. Weiter ist die
Standardabweichung des Mittelwertes
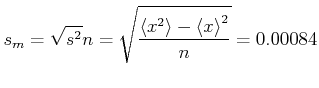 |
(6.74) |
Man erwartet für einen homogenen Würfel (
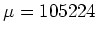 ) die Standardabweichung
) die Standardabweichung
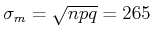 |
(6.75) |
Die beobachtete Abweichung ist jedoch 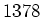 , also
, also 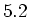 mal grösser als
mal grösser als 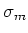 . Damit dürfte der Würfel mit
ziemlicher Sicherheit nicht homogen sein. Dieser einfache Test kann gut zu einer ersten Abschätzung der Güte einer
Messung dienen.
. Damit dürfte der Würfel mit
ziemlicher Sicherheit nicht homogen sein. Dieser einfache Test kann gut zu einer ersten Abschätzung der Güte einer
Messung dienen.
Ein weiterer einfacher Test benutzt den Vergleich der höheren Momente. Für diesen Dispersionsindex gilt
 |
(6.76) |
Unterabschnitte





Next: t-Test
Up: Vorlesungsskript Einführung in die
Previous: Lorentz-Verteilung
Othmar Marti
Experimentelle Physik
Universiät Ulm