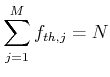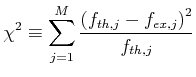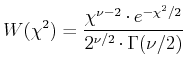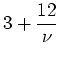Weiter: Fehlerfortpflanzung
Oben: Statistische Tests
Zurück: F-Test
Beim 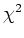 -Test liefert ein allgemeines Kriterium für die Übereinstimmung der Grundgesamtheit mit der
Stichprobe. Der
-Test liefert ein allgemeines Kriterium für die Übereinstimmung der Grundgesamtheit mit der
Stichprobe. Der 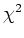 -Test taugt für jede Verteilungsfunktion, ist also modellfrei. Das Vorgehen ist
folgendermassen:
-Test taugt für jede Verteilungsfunktion, ist also modellfrei. Das Vorgehen ist
folgendermassen:
- Man ordnet die Messwerte in Klassen, so dass in jede Klasse mindestens
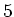 Werte fallen. Die Anzahl
Beobachtungen sei
Werte fallen. Die Anzahl
Beobachtungen sei 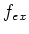
- Es sollen mindestens
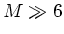 Klassen vorhanden sein.
Klassen vorhanden sein.
- Aus der Hypothese, der Verteilungsfunktion, die man testen möchte, berechnet man die erwartete Häufigkeit
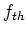 für jede Klasse, das heisst, man berechnet aus der Klassenbreite, dem Klassenmittelwert und der Dichte
der Verteilungsfunktion die erwartete Häufigkeit
für jede Klasse, das heisst, man berechnet aus der Klassenbreite, dem Klassenmittelwert und der Dichte
der Verteilungsfunktion die erwartete Häufigkeit 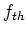 .
.
- Normierung:
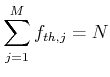 |
(6.84) |
- Die Grösse
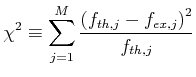 |
(6.85) |
ist ein integrales Mass für die statistischen Abweichungen der beobachteten Häufigkeiten.
Die Verteilungsfunktion lautet:
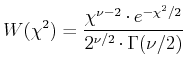 |
(6.86) |
Die kennzeichnenden Grössen sind:
Die 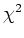 -Verteilungsfunktion ist verwandt mit der Poisson-Verteilung: sie geht für grosse
-Verteilungsfunktion ist verwandt mit der Poisson-Verteilung: sie geht für grosse 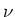 in die
Normalverteilung über. Wir rechnen nun die Wahrscheinlichkeit für den
in die
Normalverteilung über. Wir rechnen nun die Wahrscheinlichkeit für den 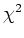 -Wert aus der Probe aus. Der Test,
ob die Stichprobe zur hypothetischen Grundgesamteit passt, gilt als bestanden, wenn die Wahrscheinlichkeit
-Wert aus der Probe aus. Der Test,
ob die Stichprobe zur hypothetischen Grundgesamteit passt, gilt als bestanden, wenn die Wahrscheinlichkeit 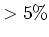 ist. Für die Anzahl Freiheitsgrade gilt:
ist. Für die Anzahl Freiheitsgrade gilt:
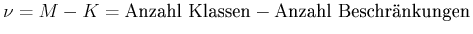 |
(6.88) |
Solche Beschränkungen sind die Normierung von 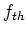 und die Mittelwertbildung. Für den
und die Mittelwertbildung. Für den 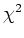 -Test ergibt
sich demnach
-Test ergibt
sich demnach
- Normal Verteilung:
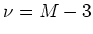
- Poisson-Verteilung:
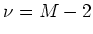
- Modellverteilungen mit a priori-Annahmen über
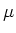 und
und 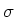 :
: 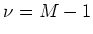 .
.
Wenn ich bei einer Stichprobe mit 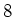 Messwerten ausrechne, dass der Mittelwert
Messwerten ausrechne, dass der Mittelwert
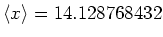 und die Standardabweichung
und die Standardabweichung
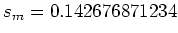 ist, so wäre eine Resultatangabe
von
vollkommen unsinnig. Ist der Fehler nämlich normalverteilt, so erhält man für
ist, so wäre eine Resultatangabe
von
vollkommen unsinnig. Ist der Fehler nämlich normalverteilt, so erhält man für
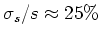 . Also sind
. Also sind 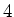 Stellen für den Mittelwert und
Stellen für den Mittelwert und 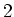 für die Abweichung angebracht:
für die Abweichung angebracht:





Next: Fehlerfortpflanzung
Up: Statistische Tests
Previous: F-Test
Othmar Marti
Experimentelle Physik
Universiät Ulm
![]() -Test liefert ein allgemeines Kriterium für die Übereinstimmung der Grundgesamtheit mit der
Stichprobe. Der
-Test liefert ein allgemeines Kriterium für die Übereinstimmung der Grundgesamtheit mit der
Stichprobe. Der ![]() -Test taugt für jede Verteilungsfunktion, ist also modellfrei. Das Vorgehen ist
folgendermassen:
-Test taugt für jede Verteilungsfunktion, ist also modellfrei. Das Vorgehen ist
folgendermassen: