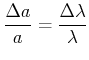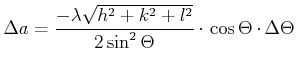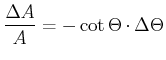Weiter: Statistische Fehler
Oben: Fehlerfortpflanzung
Zurück: Fehlerfortpflanzung
Unterabschnitte
Die direkt gemessenen Grössen
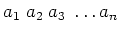 seien mit den systematischen Fehlern
seien mit den systematischen Fehlern
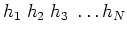 verfälscht. Gesucht ist die wahre Grösse
verfälscht. Gesucht ist die wahre Grösse 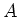 , die eine Funktion der
, die eine Funktion der 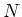 gemessenen Werte ist. Wir haben aber die
verfälschte Grösse
gemessenen Werte ist. Wir haben aber die
verfälschte Grösse 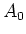 bestimmt. Für sie gilt, nach einer Taylor-Entwicklung
bestimmt. Für sie gilt, nach einer Taylor-Entwicklung
wobei bei allen Ableitungen wie üblich alle Variablen, ausser der, nach der abgeleitet wird, konstant zu halten
sind.
Da in aller Regel die Fehler klein gegen die gemessenen Werte sind, darf mit der linearen Näherung gerechnet
werden. Also lautet das Fehlerfortpflanzungsgesetz für systematische Fehler
Beim Übergang zu den relativen Fehlern erhält man:
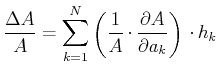 |
(7.93) |
- Summe oder Differenz:
- Wenn
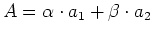 ist, dann ist
ist, dann ist
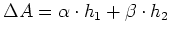
- Produkte:
- Für
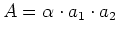 ergibt sich
ergibt sich
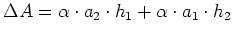 .
Einfacher ist die Gleichung mit den relativen Fehlern:
.
Einfacher ist die Gleichung mit den relativen Fehlern:
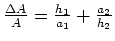
- Beliebige Potenzen:
- Bei beliebigen Potenzen gilt für
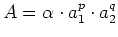 dass der relative
Fehler
dass der relative
Fehler
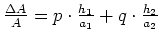 ist. (Dies erhält man mit der logarithmischen
Ableitung)
ist. (Dies erhält man mit der logarithmischen
Ableitung)
- Quotienten:
- Für
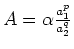 ergibt sich:
ergibt sich:
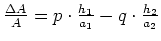
Beim Beispiel in der Einleitung erhält man für die Auswirkung der
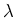 -Fehler:
-Fehler:
und für den Fehler der Gitterkonstante
oder
Daraus schliesst man, dass bei 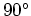 (Fall der Rückstreuung) der Fehler minimal ist. Hier ist ein Beispiel,
das zeigt, dass mit einer geschickten Wahl der experimentellen Anordnung der Messfehler minimal gemacht werden
kann.
(Fall der Rückstreuung) der Fehler minimal ist. Hier ist ein Beispiel,
das zeigt, dass mit einer geschickten Wahl der experimentellen Anordnung der Messfehler minimal gemacht werden
kann.





Next: Statistische Fehler
Up: Fehlerfortpflanzung
Previous: Fehlerfortpflanzung
Othmar Marti
Experimentelle Physik
Universiät Ulm
![]() seien mit den systematischen Fehlern
seien mit den systematischen Fehlern
![]() verfälscht. Gesucht ist die wahre Grösse
verfälscht. Gesucht ist die wahre Grösse ![]() , die eine Funktion der
, die eine Funktion der ![]() gemessenen Werte ist. Wir haben aber die
verfälschte Grösse
gemessenen Werte ist. Wir haben aber die
verfälschte Grösse ![]() bestimmt. Für sie gilt, nach einer Taylor-Entwicklung
bestimmt. Für sie gilt, nach einer Taylor-Entwicklung
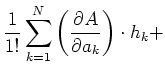
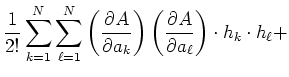
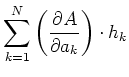
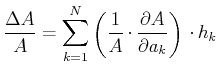
![]() -Fehler:
-Fehler: