



Weiter: Angabe von zufälligen Fehlern
Oben: Fehlerfortpflanzung
Zurück: Systematische Fehler
Unterabschnitte
Wir nehmen wieder an, dass die gesuchte Grösse 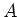 aus den direkt gemessenen Grössen
aus den direkt gemessenen Grössen
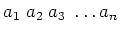 bestimmt sei. Diese seien mit zufälligen Fehlern behaftet. Wenn
bestimmt sei. Diese seien mit zufälligen Fehlern behaftet. Wenn 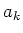
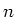 -mal gemessen wurde, so bezeichnen
wir die
-mal gemessen wurde, so bezeichnen
wir die 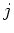 -te Messung der
-te Messung der 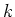 -ten Grösse mit
-ten Grösse mit 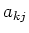 . Der Mittelwert von
. Der Mittelwert von 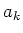 ist
ist
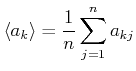 |
(7.94) |
und die Varianz
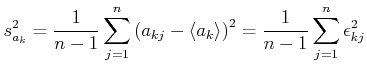 |
(7.95) |
wobei
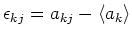 der Fehler von
der Fehler von 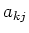 bezüglich
bezüglich
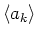 ist.
ist.
Es gibt nun zwei Wege, wie wir von den gemessenen Grössen auf das Endresultat kommen können. Sind die
beiden Wege äquivalent?
Wir können zuerst jede einzelne Messung mitteln, und dann in unsere Funktion für das Endresultat einsetzen.
Wir können auch jeweils die 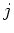 -te Wiederholung der Messung einsetzen und dann mitteln.
Nun lässt sich der Wert von
-te Wiederholung der Messung einsetzen und dann mitteln.
Nun lässt sich der Wert von 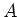 , durch eine Taylor-Entwicklung angeben.
, durch eine Taylor-Entwicklung angeben.
Wenn der Betrag der Abweichungen von den Mittelwerten klein sind gegen den Betrag der Mittelwerte, haben wir
Wenn wir nun im 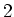 . Glied die Reihenfolge der Summation vertauschen, dann finden wir
Also gilt:
. Glied die Reihenfolge der Summation vertauschen, dann finden wir
Also gilt:
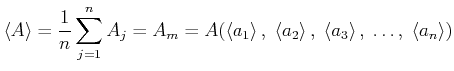 |
(7.96) |
Die obige Formel gilt ziemlich allgemein, z.B. auch wenn nicht alle Teilresultate gleich häufig gemessen wurden.
Wir nehmen an, dass die Varianzen 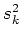 der gemittelten Messwerte
der gemittelten Messwerte 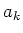 bekannt seien. Die Varianzen sind, nach der allgemeinen Definition,
bekannt seien. Die Varianzen sind, nach der allgemeinen Definition,
Wenn die Messungen der 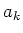 voneinander statistisch unabhängig sind, dann summieren sich alle Kreuzprodukte zu
0. Also lautet das Gausssche Fehlerfortpflanzungsgesetz
voneinander statistisch unabhängig sind, dann summieren sich alle Kreuzprodukte zu
0. Also lautet das Gausssche Fehlerfortpflanzungsgesetz
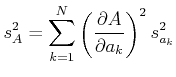 |
(7.98) |
Teilen wir beide Seiten mit 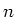 , erhält man das Fehlerfortpflanzungsgesetz für die mittleren Fehler der
Mittelwerte, die in der Praxis am meisten angewandte Form.
, erhält man das Fehlerfortpflanzungsgesetz für die mittleren Fehler der
Mittelwerte, die in der Praxis am meisten angewandte Form.
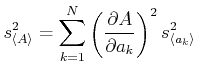 |
(7.99) |
Wenn die Messwerte 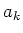 statistisch unabhängig sind, dann treten in
statistisch unabhängig sind, dann treten in
positive und negative Zeichen mit gleicher Häufigkeit auf. Wenn diese Summe null ist, nennt man die beiden
Messgrössen 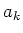 und
und 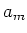 statistisch unabhängig. Dies wird mit dem Begriff der Kovarianz beschrieben
statistisch unabhängig. Dies wird mit dem Begriff der Kovarianz beschrieben
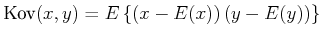 |
(7.100) |
wobei der Operator 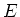 den Erwartungswert berechnet. Wieder gilt, dass wenn die Grössen
den Erwartungswert berechnet. Wieder gilt, dass wenn die Grössen 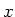 und
und 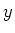 voneinander
statistisch unabhängig sind, dass die Produkte in der Summe für den Erwartungswert mit gleicher Häufigkeit beide
Vorzeichen annehmen.
voneinander
statistisch unabhängig sind, dass die Produkte in der Summe für den Erwartungswert mit gleicher Häufigkeit beide
Vorzeichen annehmen.
Wenn wir eine vollständige Korrelation haben, also
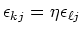 ist, dann gilt
ist, dann gilt
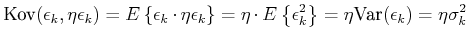 |
(7.101) |
Die Kovarianz geht also im Falle einer vollständigen Korrelation
in die Varianz über.
Das Gausssche Fehlerfortpflanzungsgesetz darf nicht angewandt
werden, wenn Korrelationen existieren (angezeigt durch die Kovarianz)
- Physikalische Korrelationen: zum Beispiel wenn gleichzeitig Strom und Spannung gemessen werden.
- Algebraische Korrelationen: Die Physikalischen Grundkonstanten sind korreliert. Man muss in
diesem Falle die Fehlermatrix berechnen (Siehe Gränicher[Grä81])
|




Next: Angabe von zufälligen Fehlern
Up: Fehlerfortpflanzung
Previous: Systematische Fehler
Othmar Marti
Experimentelle Physik
Universiät Ulm
![]() aus den direkt gemessenen Grössen
aus den direkt gemessenen Grössen
![]() bestimmt sei. Diese seien mit zufälligen Fehlern behaftet. Wenn
bestimmt sei. Diese seien mit zufälligen Fehlern behaftet. Wenn ![]()
![]() -mal gemessen wurde, so bezeichnen
wir die
-mal gemessen wurde, so bezeichnen
wir die ![]() -te Messung der
-te Messung der ![]() -ten Grösse mit
-ten Grösse mit ![]() . Der Mittelwert von
. Der Mittelwert von ![]() ist
ist
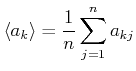
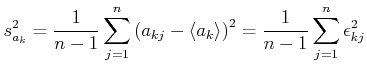
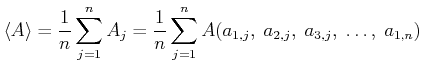
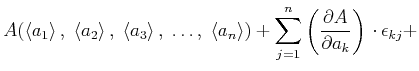
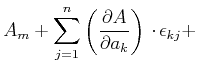
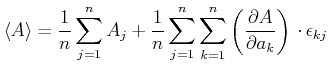
![]() der gemittelten Messwerte
der gemittelten Messwerte ![]() bekannt seien. Die Varianzen sind, nach der allgemeinen Definition,
bekannt seien. Die Varianzen sind, nach der allgemeinen Definition,
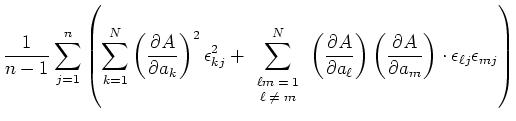
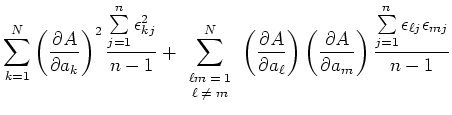
![]() voneinander statistisch unabhängig sind, dann summieren sich alle Kreuzprodukte zu
0. Also lautet das Gausssche Fehlerfortpflanzungsgesetz
voneinander statistisch unabhängig sind, dann summieren sich alle Kreuzprodukte zu
0. Also lautet das Gausssche Fehlerfortpflanzungsgesetz
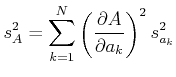
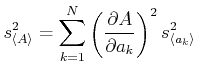
![]() statistisch unabhängig sind, dann treten in
statistisch unabhängig sind, dann treten in
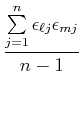
![]() ist, dann gilt
ist, dann gilt