| (7.102) |
Da nach dem Gaussschen Fehlerfortpflanzungsgesetz positive und negative Fehler gleich häufig vorkommen, muss der Fehler wie folgt angegeben werden:
| (7.102) |
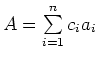 ergibt
ergibt
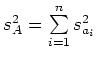
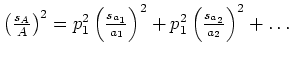
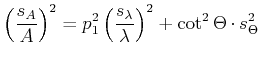
Will man nicht so viel rechnen, dann verwendet man die zu der Fehlerfortpflanzung bei systematischen Fehlern verwendete Funktion, bildet aber von jedem Summanden den Betrag. Die Berechnung des maximalen Fehlers ist schnell, ergibt aber in den meisten Fällen einen bis zu dreimal zu grossen Fehler, eine Tatsache die sich in der Wirtschaft nicht rechnet!