Weiter: Relativität Oben: Mechanik Zurück: Zentralbewegung Skript: PDF-Datei Übungen: Blätter
Unter Gravitation versteht man die gegenseitige Anziehung der Körper durch ihre Massen.
Beweis: des 2. Gesetzes
Es gibt keine äusseren Kräfte, deshalb gibt es auch keine Drehmomente. Aus ![]() bekommt man :
bekommt man :
![]()
![\includegraphics[width=0.5\textwidth]{mechanik-059}](img1071.gif)
2. Keplersches Gesetz
|
Behauptung: Für die Fläche
![]() gilt
gilt
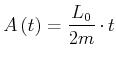 |
(3.287) |
Beweis:
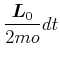 |
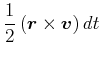 |
(3.288) | |
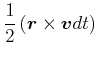 |
(3.289) | ||
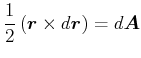 |
(3.290) |
Bemerkung: bei einer ebenen Bewegung ist immer
| (3.291) | |||
| (3.292) |
d.h. das 2. Keplersche Gesetz entspricht der Drehimpulserhaltung
|
|
|
|
![\includegraphics[width=0.5\textwidth]{mechanik-060}](img1081.gif)
Newtonsches Gravitationsgesetz
|
Die Kraft der Masse ![]() auf die Masse
auf die Masse ![]() ist
ist
![]() , also
, also
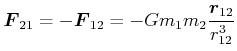 |
(3.293) |
Betragsmässig:
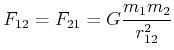 |
(3.294) |
Dabei ist
![]() die
Gravitationskonstante. Das Newtonsche Gravitationsgesetz definiert die
schweren Masse, im Gegensatz zum 2. Newtonschen Gesetz der Bewegung
(
die
Gravitationskonstante. Das Newtonsche Gravitationsgesetz definiert die
schweren Masse, im Gegensatz zum 2. Newtonschen Gesetz der Bewegung
(
![]() ), das die träge Masse definiert.
), das die träge Masse definiert.
Testmasse ![]()
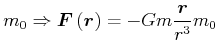 |
(3.295) |
Feldvektor
![]() ist der Feldvektor des Gravitationsfeldes
ist der Feldvektor des Gravitationsfeldes
![]() ist unabhängig von der Testmasse
ist unabhängig von der Testmasse ![]()
Behauptung:
![]() ist konservativ
ist konservativ
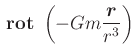 |
(3.297) | ||
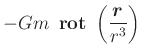 |
(3.298) | ||
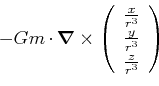 |
(3.299) | ||
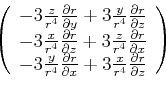 |
(3.300) | ||
| (3.301) |
da gilt
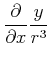 |
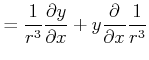 |
|
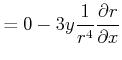 |
||
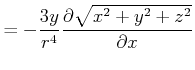 |
||
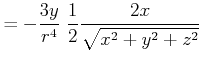 |
||
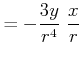 |
Damit ist
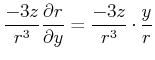 |
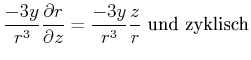 |
(3.302) |
Das heisst, es existiert eine potentielle Energie
Def.
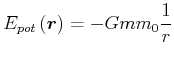 |
(3.303) |
wobei wir den Energienullpunkt ins Unendliche legen.
Beweis: Berechnung der Arbeit gegen die Feldkraft längs einer Feldlinie
![\includegraphics[width=0.71\textwidth]{mechanik-061}](img1106.gif)
|
Bei der Berechnung der potentiellen Energie muss man berücksichtigen, dass die
Kraft ![]() und
und ![]() entgegengesetzt angeordnet sind. Da das
Gravitationsfeld konservativ ist, können wir eine ganz spezielle Bahn
verwenden. Zwischen zwei beliebigen Punkten
entgegengesetzt angeordnet sind. Da das
Gravitationsfeld konservativ ist, können wir eine ganz spezielle Bahn
verwenden. Zwischen zwei beliebigen Punkten ![]() und
und ![]() lassen
wir die Bahn von
lassen
wir die Bahn von ![]() bis zu der Kugelschale um den Massenpunkt
bis zu der Kugelschale um den Massenpunkt ![]() , auf
der
, auf
der ![]() liegt, laufen und führen sie dann auf der Kugelschale zu
liegt, laufen und führen sie dann auf der Kugelschale zu
![]() . Auf dem auf der Kugelschale liegenden Teil ist
. Auf dem auf der Kugelschale liegenden Teil ist ![]() senkrecht auf
senkrecht auf ![]() , so dass
, so dass
![]() ist: dieser
Bahnabschnitt trägt nichts zur potentiellen Energie bei.
ist: dieser
Bahnabschnitt trägt nichts zur potentiellen Energie bei.
Also haben wir
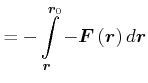 |
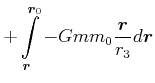 |
|||
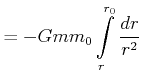 |
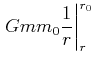 |
|||
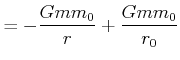 |
(3.304) |
Es ist üblich, den Referenzpunkt
![]() zu setzen:
zu setzen:
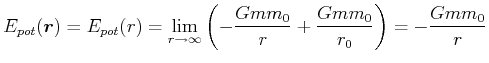 |
(3.305) |
Damit ist die Behauptung gezeigt.
Die potentielle Energie hängt von der Testmasse ![]() ab.
ab.
Wir definieren das Testmassen-unabhängige Gravitationspotential
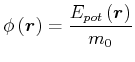 |
(3.306) |
dann gilt:
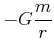 |
(3.307) | ||
| (3.308) | |||
| (3.309) |
![\includegraphics[width=0.4\textwidth]{mechanik-062}](img1128.gif)
Oberflächenintegrale: Definition der Grössen
|
Normalenvektor
![]()
Oberflächenelement in Kugelkoordination
| (3.310) |
dabei ist
![]() die horizontale Seite des Flächenelementes,
die horizontale Seite des Flächenelementes, ![]() die vertikale Seite.
die vertikale Seite.
![\includegraphics[width=0.42\textwidth]{mechanik-063}](img1133.gif)
Koordinaten des Oberflächenelementes
|
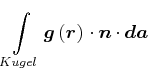 |
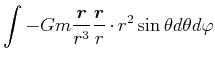 |
(3.311) | |
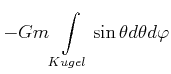 |
(3.312) | ||
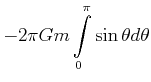 |
(3.313) | ||
| (3.314) |
also
|
Die in einer Kugel (beliebigen Fläche) eingeschlossene Masse kann aus dem Integral über
![]() an der Oberfläche bestimmt werden. Damit kann man über die Keplerschen Gesetze mit einer
Testmasse (Satellit) die Masse eines Himmelskörpers bestimmen!
an der Oberfläche bestimmt werden. Damit kann man über die Keplerschen Gesetze mit einer
Testmasse (Satellit) die Masse eines Himmelskörpers bestimmen!
Betrachte ![]() Massenpunkt mit
Massenpunkt mit ![]() an den Orten
an den Orten
![]()
![\includegraphics[width=0.7\textwidth]{mechanik-064}](img1143.gif)
Anordnung von Massenpunkten
|
Es gilt
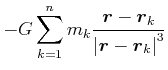 |
(3.316) | ||
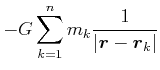 |
(3.317) |
Da die einzelnen Teilfelder konservativ sind, ist auch das Gesamtfeld konservativ.
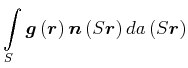 |
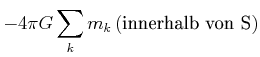 |
(3.318) | |
| (3.319) |
![\includegraphics[width=0.7\textwidth]{mechanik-065}](img1149.gif)
Koordinaten zur Berechnung eines Oberflächenintegrals
|
Kontinuierliche Massenverteilung: gegeben durch Massendichte
![]()
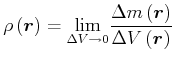 |
(3.320) |
Berechnung der Gesamtmasse aus Dichte:
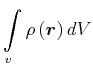 |
(3.321) | ||
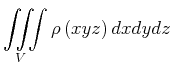 |
(3.322) |
In Kugelkoordinaten wäre
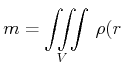 , , |
(3.323) |
Oberflächenintegral
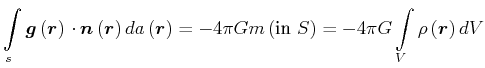 |
(3.324) |
Für kontinuierliche Massenverteilungen gilt die Feldgleichungen der Gravitation
| (3.325) |
Def:
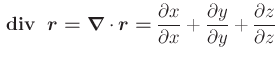 |
(3.326) |
Beweis: Nach Gauss gilt:
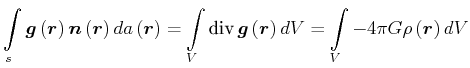 |
(3.327) |
Die Lösung der Feldgleichung ist
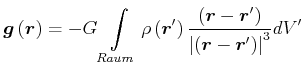 |
(3.328) |
Dabei ist ![]() das Volumenelement am Ort
das Volumenelement am Ort ![]() . Die Lösung hat die
gleiche Struktur wie das Gesetz für den Feldvektor der Gravitation,
Gleichung (3.221) . Die ist leicht zu sehen, wenn man die Variablen wie folgt
umschreibt:
. Die Lösung hat die
gleiche Struktur wie das Gesetz für den Feldvektor der Gravitation,
Gleichung (3.221) . Die ist leicht zu sehen, wenn man die Variablen wie folgt
umschreibt:
Da
![]() gilt
gilt
| (3.329) | |||
| (3.330) | |||
| (3.331) |
also
heisst Poisson-Gleichung |
![]() heisst Laplace-Operator:
heisst Laplace-Operator:
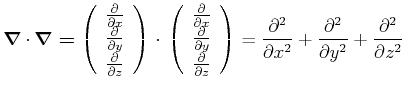 |
(3.333) |
Formal ist die Lösung der Poissongleichung
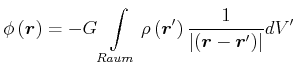 |
(3.334) |
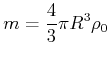 |
(3.335) |
bei konstanter Dichte ![]()
![\includegraphics[width=0.7\textwidth]{mechanik-066}](img1180.gif)
|
Wir unterscheiden die folgenden Fälle:
|
Behauptung: Nur die Masse innerhalb der Kugelschale beeinflusst die Gravitationskraft
![\includegraphics[width=0.46\textwidth]{gravitationsfeldvektor}](img1190.gif)
![\includegraphics[width=0.46\textwidth]{gravitationspotential}](img1191.gif)
Links wird der Verlauf des Gravitationsfeldvektors
gezeigt, rechts der des dazugehörigen Gravitationspotentials. Beide sind für eine massive homogene Kugel mit dem
Radius 1 gerechnet.
|
Im Folgenden werden zwei Beweisarten gezeigt:
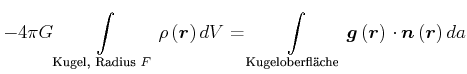 |
(3.336) |
mit
da
![]() ist. Also ist
ist. Also ist
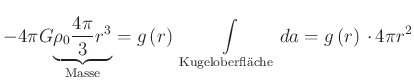 |
(3.337) |
Innerhalb der kugelförmigen Masse gilt also
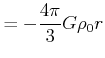 |
||
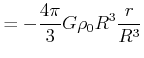 |
||
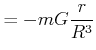 |
(3.338) |
Ausserhalb erhalten wir
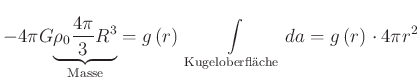 |
(3.339) |
oder
| (3.340) | ||
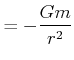 |
(3.341) |
Aus diesen Gleichungen kann das Potential berechnet werden.
Dazu verwendet man die Definition der potentiellen Energie für ein radialsymmetrisches Potential
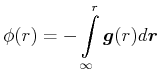
Für ausserhalb bekommt man
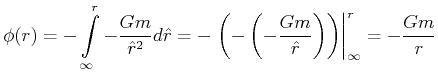
Innerhalb der Kugel verwendet man den Radius der Kugel ![]() als Referenz
als Referenz
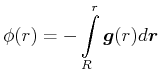
und damit
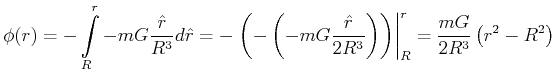
Für die Distanz ![]() muss das Potential kontinuierlich sein. Wir führen eine Konstante
muss das Potential kontinuierlich sein. Wir führen eine Konstante ![]() ein und setzen
ein und setzen
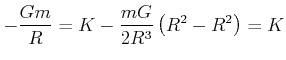
Also ist für Innen das Resultat
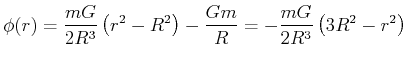
Das Schlussresultat ist
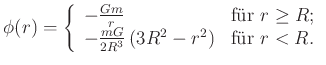 |
(3.342) |
Gravitationskraft eines Kreisringes
![\includegraphics[width=0.7\textwidth]{gravitation-001}](img1211.gif)
Berechnung des Kreisringes
|
Symmetrie: nur ![]() -Komponente betrachten
-Komponente betrachten
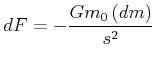 |
(3.343) |
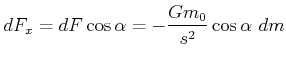 |
(3.344) |
Die ![]() -Komponente des Feldvektors der Gravitation ist nun (betragsmässig):
-Komponente des Feldvektors der Gravitation ist nun (betragsmässig):
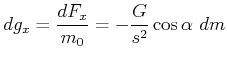 |
(3.345) |
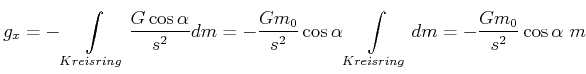 |
(3.346) |
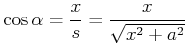 |
(3.347) |
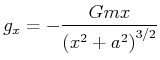 |
(3.348) |
![\includegraphics[width=0.7\textwidth]{gravitation-002}](img1219.gif)
Berechnung einer Kugelschale zusammengesetzt aus Kreisringen
|
|
Daraus ergibt sich:
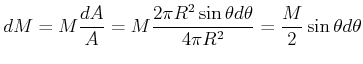 |
(3.349) |
und mit
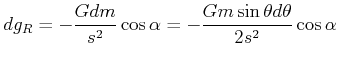 |
(3.350) |
| (3.351) |
oder
| (3.352) |
| (3.353) |
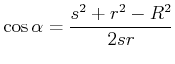 |
(3.354) |
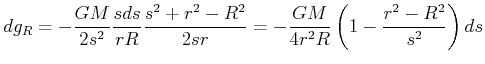 |
(3.355) |
![$\displaystyle g_{R}=-\frac{GM}{4r^{2}R}\int\limits_{r-R}^{r+R}\left( 1-\frac{r^...
...right) ds=-\frac{GM}{4r^{2}R}\left[ s-\frac{r^{2}-R^{2}}{s}\right] _{r-R}^{r+R}$](img1236.gif) |
(3.356) |
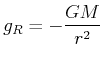 |
(3.357) |
Den Feldvektor der Gravitation für einen Punkt innerhalb einer Vollschale kann jetzt noch durch Integration über alle eingeschlossenen Unterschalen erhalten werden, deren Radien kleiner sind als der Radius des betrachteten Punktes. An der Form des Resultates ändert sich nichts mehr.
Das Gewicht oder die Gewichtskraft
![]() einer Masse
einer Masse ![]() wird durch die Gravitation
zwischen der Erde und
wird durch die Gravitation
zwischen der Erde und ![]() bewirkt.
bewirkt.
Modell: Die Erde entspricht einer Kugel. Dann gilt an der Oberfläche
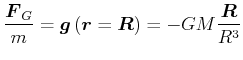 |
(3.358) |
Im Labor ist
![]()
und
![]()
Freier Fall:
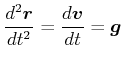 |
(3.359) |
mit
![]() und
und
![]() bekommt man
bekommt man
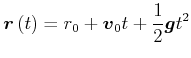 |
(3.360) |
![\includegraphics[width=0.4\textwidth]{mechanik-070}](img1249.gif)
|
|
|
![]() beschleunigt die Masse, also gilt:
beschleunigt die Masse, also gilt:
| (3.361) |
| (3.362) |
Bewegungsgleichung
| (3.363) |
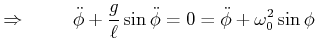 |
(3.364) |
mit
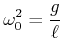 |
(3.365) |
Kleine Auslenkungen:
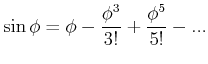 |
(3.366) |
also
| (3.367) |
harmonische Schwingung:
| (3.368) |
Beweis
| (3.369) |
d.h. die Bewegungsgleichung ist erfüllt.
![]() und
und ![]() hängen von den Anfangsbedingungen ab.
hängen von den Anfangsbedingungen ab.
Beispiel: Freier Fall
| von | |
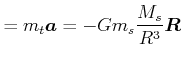 |
(3.370) | |
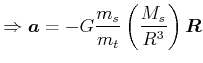 |
(3.371) |
Beobachtung
![]() ist unabhängig vom Material
ist unabhängig vom Material
Experimentell:
![]()
Herleitung des 3. Keplerschen Gesetzes, mit Kreisbahnen
![\includegraphics[width=0.5\textwidth]{mechanik-071}](img1268.gif)
Herleitung des 3. Keplerschen Gesetzes
|
Zentripetalkraft
![]()
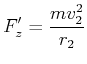 |
(3.372) |
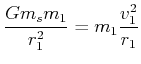 |
(3.373) |
nun ist die Umlaufszeit
![]() oder
oder
![]()
also ist
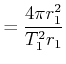 |
(3.374) | |
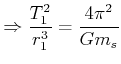 |
(3.375) |
Dies ist das 3. Keplersche Gesetz.
Maximale Höhe eines Satelliten
Wir wissen
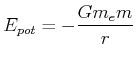 |
(3.376) |
Energiesatz:
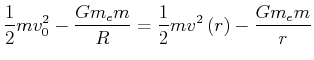
wobei ![]() der Erdradius ist.
der Erdradius ist.
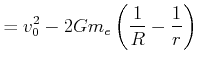 |
(3.377) | |
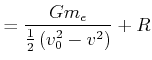 |
(3.378) |
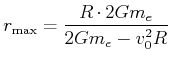 |
(3.379) |
![]() divergiert wenn
divergiert wenn
![]()
oder mit
![]() bekommt man die Fluchtgeschwindigkeit
bekommt man die Fluchtgeschwindigkeit
Gesamtenergie eines Satelliten
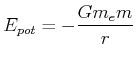 |
(3.380) |
Zentripetalkraft
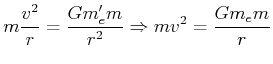 |
(3.381) |
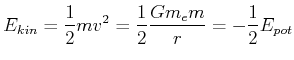 |
(3.382) |
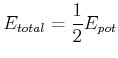 |
(3.383) |
Othmar Marti