Wärmekapazität bei konstantem Druck

Aus dem idealen Gasgesetz (Gleichung (4.29) ) folgt bei konstantem Druck $p$ und Teilchenzahl $N$, dass

$$p\; dV = Nk\; dT = \nu R\; dT$$

ist.

Der erste Hauptsatz (Gleichung (4.35) ) besagt, dass

$$\delta Q=d U+p\; d V$$

sei.

Setzen wir die Definition für die Wärmekapazität bei konstantem Volumen (Gleichung (4.18) ) und das ideale Gasgesetz ein, so erhalten wir

$$\delta Q = \nu c_{V\text{,} mol}\; dT + \nu R\; dT = \nu\left[c_{V\text{,} mol}+R\right]\; dT$$

Andererseits ist die Wärmezufuhr pro Mol bei konstantem Volumen gegeben durch

$$\delta Q = c_{V\text{,} mol}\; d T=\frac{f}{2}R \; d T$$

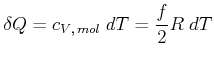Also erhält man pro Mol

$$c_{p\text{,} mol}\; dT = \left[c_{V\text{,} mol}+R\right]\;dT =\left( \frac{f}{2}+1\right)R\; dT$$

Zwischen $c_{p\text{,} mol}$ und $c_{V\text{,} mol}$ besteht die Beziehung

$$c_{p\text{,} mol} = \left(\frac{f}{2}+1\right)R$$ (4.318)

Aus den Zeiten vor dem SI-System kennt man das Wärmeäquivalent

$$1\;kcal =4.1\;kJ$$

$$1\;cal = 4.1\;J$$

das die Einheit $kcal$ (Kilokalorie) mit der Einheit Joule verknüft.

Adiabatenexponent

Bei schnellen Zustandsänderungen in Gasen (zum Beispiel bei Schallwellen) kann ein thermodynamisches System sich nicht mit der Umgebung durch Wärmeaustausch ins Gleichgewicht bringen. Für diese adiabatischen Zustandsänderungen gilt

$$\delta Q = 0$$

Wir erhalten aus der idealen Gasgleichung (Gleichung (4.29) )

$$\delta W = - p\; dV = -p(V)\; dV = - \frac{\nu RT}{V} dV = - \nu RT \frac{dV}{V}$$

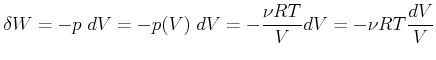Die Wärmezufuhr wird durch

$$0 = \delta Q = dU - \delta W = dU + p\; dV = \nu c_{V\text{,} mol} dT + p\; dV$$

beschrieben. Aus diesen beiden Gleichungen erhält man durch Kombination

$$0 = \nu c_{V\text{,} mol} dT + \nu RT \frac{dV}{V}$$

Wir teilen durch $T$ und eliminieren $\nu$

$$0 = c_{V\text{,} mol}\frac{dT}{T}+ R\frac{dV}{V}$$ (4.319)

Aus dieser Gleichung folgt durch Integrieren

$$-\int\limits_{T_0}^T c_{V\text{,} mol}\frac{dT}{T} = \int\limits_{V_0}^V R\frac{dV}{V}$$

und

$$-c_{V\text{,} mol}\ln(T)+c_{V\text{,} mol}\ln(T_0)= R\ln(V)- R\ln(V_0)$$

Daraus erhalten wir die Beziehung

$$-c_{V\text{,} mol}\ln\left(\frac{T}{T_0}\right)= R\ln\left(\frac{V}{V_0}\right)$$ (4.320)

oder auch

$$T^{c_{V\text{,} mol}}\cdot V^R = const = T_0^{c_{V\text{,} mol}}\cdot V_0^R$$

Dies kann auch als

$$\left(\frac{T}{T_0}\right)^{-c_{V\text{,} mol}} = \left(\frac{V}{V_0}\right)^R$$

umgeschrieben werden. Mit $c_{V\text{,} mol} = \frac{f}{2}R$ bekommt man durch Ziehen der $R$-ten Wurzel

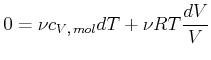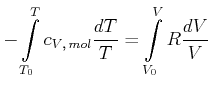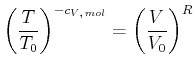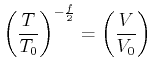$$\left( \frac{T}{T_{0}}\right) ^{-\frac{f}{2}}=\left( \frac{V}{ V_{0}}\right)$$ (4.321)

Wir definieren nun den Adiabatenexponenten

$$\gamma =\frac{c_{p\text{,} mol}}{c_{V\text{,} mol}}=\frac{c_{V\... ...}+ R}{c_{V\text{,} mol}} =\frac{\frac{f}{2}R + R}{\frac{f}{2}R} =\frac{f+2}{f}$$ (4.322)

Umgeschrieben lautet die Gleichung

$$\frac{f}{2} = \frac{1}{\gamma-1}$$

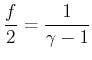Damit bekommen wir die Gleichung

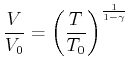$$\frac{V}{V_{0}}=\left( \frac{T}{T_{0}}\right) ^{\frac{1}{1-\gamma }}$$ (4.323)

oder, umgekehrt

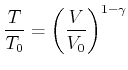$$\frac{T}{T_{0}}=\left( \frac{V}{V_{0}}\right) ^{1-\gamma }$$ (4.324)

Aus der Gleichung (4.29) für das ideale Gas folgt

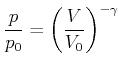$$\frac{p}{p_{0}} =\left( \frac{V}{V_{0}}\right) ^{-\gamma }$$ (4.325)

und

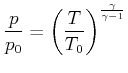$$\frac{p}{p_{0}}=\left( \frac{T}{T_{0}}\right) ^{\frac{\gamma }{\gamma -1}}$$ (4.326)

Da bei einem Adiabatischen Prozess wie der Schallausbreitung in der Atmosphäre keine Energie ausgetauscht wird, gilt

$$pV^{\gamma } = const$$

und nicht, wie man aus der idealen Gasgleichung entnehmen würde

$$pV=const$$

Die ideale Gasgleichung gilt nur bei quasistatischen Prozessen mit Energieaustausch, nicht aber bei adiabatischen Prozessen (d. h., bei Prozessen ohne Energieaustausch.

Zustandsdiagramme

Prozesse werden mit Zustandsdiagrammen beschrieben:

Zustandsdiagramm $T\left( p,V\right)$ für das ideale Gas und adiabatische Änderungen für die Anzahl Freiheitsgrade $f=3$, $f=5$, $f=6$ und $f=20$.

Adiabatische Prozesse nähern sich mit höheren Freiheitsgraden den isothermen Prozessen an.

Doppelt logarithmische Darstellung des Zustandsdiagramms $T\left( p,V\right)$ für das ideale Gas und adiabatische Änderungen für die Anzahl Freiheitsgrade $f=3$, $f=5$, $f=6$ und $f=20$.

Darstellung der häufigsten Typen von Zustandsänderungen

Bedingung	Zustandsänderung
$V=const$	Isochore
$p=const$	Isobare
$T=const$	Isotherme
$dQ=0$	Adiabate oder Isentrope

Typische Zustandsänderungen

Die Druckarbeit bei den verschiedenen Zustandsänderungen hat jeweils die folgende Grösse:

Druckarbeit	Zustandsänderung
$\delta W=p\; d V$	isobar
$W=U_{1}-U_{2}=C_{V\text{,} {mol}}\nu \left( T_{1}-T_{2}\right)$	adiabatisch
$W=\int pdV=\nu RT\int_{V_{1}}^{V_{2}}\frac{dV}{V}=\nu R T \ln \frac{V_{2} }{V_{1}}$	isotherm
$W=0$	isochor

Druckarbeit bei typischen Zustandsänderungen