Weiter: Wärmeleitung Oben: Wärmelehre Zurück: Boltzmannverteilung und Diffusion Skript: PDF-Datei Übungen: Blätter
Eine Wärmekraftmaschine transportiert Wärme von einem Wärmebad in ein zweites mit einer niedrigeren Temperatur und gibt dabei mechanische (allgemein jede nichtthermische) Energie ab.
Bei einem Otto-Motor wird ein Luft-Benzin-Gemisch der Umgebungstemperatur ![]() angesaugt und adiabatisch auf
angesaugt und adiabatisch auf ![]() verdichtet. Dann wird dieses Gemisch
entzündet und erreicht die Temperatur
verdichtet. Dann wird dieses Gemisch
entzündet und erreicht die Temperatur ![]() . Die heissen Gase drücken einen
Kolben nach unten. Am unteren Umkehrpunkt, dem unteren Totpunkt, hat das Gas
die Temperatur
. Die heissen Gase drücken einen
Kolben nach unten. Am unteren Umkehrpunkt, dem unteren Totpunkt, hat das Gas
die Temperatur ![]() . Darauf wird das Gas an die Umgebung abgegeben. Im
. Darauf wird das Gas an die Umgebung abgegeben. Im
![]() -Diagramm sieht dies so aus:
-Diagramm sieht dies so aus:
![\includegraphics[width=0.5\textwidth]{hauptsatz_eins-005}](img1400.gif)
Arbeitszyklus eines Ottomotors.
|
![\includegraphics[width=0.7\textwidth]{hauptsatz_eins-006}](img1402.gif)
Wärmestrom vom Wärmebad (Wärmereservoir) bei
|
Beim Ottomotor kann nur der Übergang von ![]() nach
nach ![]() mechanische Arbeit
leisten. Alle anderen Übergänge sind adiabatisch, isochor oder isobar mit
Ankopplung an die Umgebungsluft.
mechanische Arbeit
leisten. Alle anderen Übergänge sind adiabatisch, isochor oder isobar mit
Ankopplung an die Umgebungsluft.
Bei ![]() ist die innere Energie
ist die innere Energie
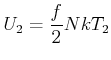 |
Bei ![]() erniedrigt sie sich auf
erniedrigt sie sich auf
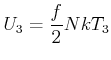 |
Die Differenz der inneren Energien
![]() wird in mechanische Energie
umgewandelt. Der Wirkungsgrad ist also
wird in mechanische Energie
umgewandelt. Der Wirkungsgrad ist also
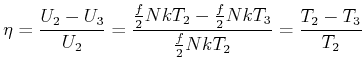 |
(4.365) |
Genauer betrachtet wird bei der Verbrennung Luft mit der Temperatur ![]() auf
auf
![]() erwärmt. Die zugeführte Energie ist
erwärmt. Die zugeführte Energie ist
![]() . Die Auspuffgase mit
der Temperatur
. Die Auspuffgase mit
der Temperatur ![]() werden an die Umgebung mit
werden an die Umgebung mit ![]() abgegeben. Der
energetische Verlust ist also
abgegeben. Der
energetische Verlust ist also
![]() . Schliesslich wird noch mechanische
Energie benötigt, um die angesaugte Luft von
. Schliesslich wird noch mechanische
Energie benötigt, um die angesaugte Luft von ![]() auf
auf ![]() zu erwärmen, also
eine Energie von der Grösse
zu erwärmen, also
eine Energie von der Grösse ![]() . Die Energiebilanz ist
. Die Energiebilanz ist
| Verbrennung | |||||
| Arbeitstakt | |||||
| Verluste an die Umwelt | |||||
| Kompression | |||||
| Bilanz der mechanischen Energie |
Der Wirkungsgrad wird in Worten so definiert:
|
Der Wirkungsgrad |
Dies bedeutet bei einer Wärmekraftmaschine, dass ![]() ist, da die
zugeführte Wärmemenge grösser ist als die abgegebene mechanische Energie. Bei
einer Kältemaschine (Kühlschrank), ist die Nutzenergie die abgeführte
thermische Energie. Zugeführt wird die mechanische Energie. Bei der
Kältemaschine ist
ist, da die
zugeführte Wärmemenge grösser ist als die abgegebene mechanische Energie. Bei
einer Kältemaschine (Kühlschrank), ist die Nutzenergie die abgeführte
thermische Energie. Zugeführt wird die mechanische Energie. Bei der
Kältemaschine ist ![]() .
.
Der Wirkungsgrad des Ottomotors ist dann (unter Berücksichtigung der Vorzeichen
Nun liegen die Temperaturen ![]() und
und ![]() auf der gleichen Adiabaten. Es
gilt also
auf der gleichen Adiabaten. Es
gilt also
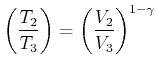 |
Da ![]() und
und ![]() auf der gleichen Adiabaten liegen, gilt auch
auf der gleichen Adiabaten liegen, gilt auch
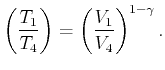 |
Weiter ist nach unserem ![]() -Diagramm (Abbildung 4.13) ist
-Diagramm (Abbildung 4.13) ist ![]() und
und ![]() , also
, also
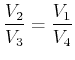 |
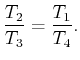 |
Deshalb muss gelten
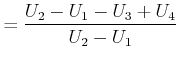 |
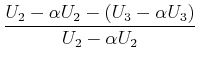 |
|||
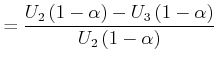 |
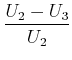 |
|||
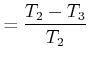 |
(4.367) |
Da die wesentlichen Takte des Otto-Zyklus adiabatisch und isochor
sind, können wir den Wirkungsgrad auch mit dem Kompressionsverhältnis ![]() (für die Drucke) ausdrücken (
(für die Drucke) ausdrücken (![]() und
und ![]() ):
):
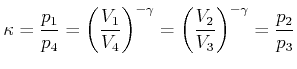 |
(4.368) |
Daraus berechnet man wie die Temperaturen vom Kompressionsverhältnis ![]() abhängen
abhängen
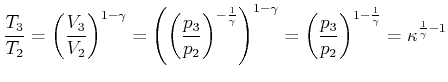 |
(4.369) |
Drücken wir den Adiabatenkoeffizienten mit der Anzahl der molekularen
Freiheitsgrade aus
![]() bekommen wir die Gleichung für den
Wirkungsgrad als Funktion des Kompressionsverhältnisses
bekommen wir die Gleichung für den
Wirkungsgrad als Funktion des Kompressionsverhältnisses
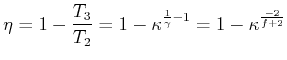 |
(4.370) |
Um für reale Motoren den Wirkungsgrad abzuschätzen, benötigen wir die Anzahl
Freiheitsgrade der Moleküle im Verbrennungsraum. Da Luft zu 80% aus Stickstoff
besteht, nehmen wir an, dass ![]() ist. Wir verwenden hier das
Volumenkompressionsverhältnis
ist. Wir verwenden hier das
Volumenkompressionsverhältnis
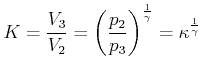 |
|
Ideale gasbetriebene Wärmekraftmaschinen haben alle den beim Otto-Motor im Abschnitt 4.8.1 angegebenen Wirkungsgrad. Theoretisch das erste mal abgeleitet wurde dieser Wirkungsgrad durch Sadi Carnot. Er benutzte eine idealisierte Wärmekraftmaschine, die heute unter dem Namen Carnot-Maschine um den Wirkungsgrad abzuleiten.
Die Carnot-Maschine verwendet vier Arbeitszyklen, zwei Isothermen und zwei Adiabaten.
![\includegraphics[width=0.7\textwidth]{carnot-prinzip}](img1454.gif)
Schematische Funktion einer Carnot-Maschine
|
Wir verwenden dabei die Definition der Entropie:
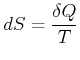 |
(4.371) |
![\includegraphics[width=0.7\textwidth]{carnot}](img1456.gif)
Arbeitsdiagramm der Carnot-Maschine
|
Die innere Energie kann nur durch Zufuhr von Wärme (![]() ) oder
mechanischer Arbeit (
) oder
mechanischer Arbeit (![]() ) geändert werden
) geändert werden
| (4.372) |
Bei Isothermen ändert sich die innere Energie nicht, das heisst, dass ![]() ist. Damit gilt für Isothermen auch
ist. Damit gilt für Isothermen auch
| (4.373) |
Bei den Adiabaten wird keine Wärme mit der Umgebung ausgetauscht. Deshalb ist
![]() . Damit sind die zugeführte mechanische Energie und die Änderung
der inneren Energie gleich.
. Damit sind die zugeführte mechanische Energie und die Änderung
der inneren Energie gleich.
| (4.374) |
Während der beiden isothermen Zustandsänderungen ist die Carnot-Maschine
jeweils an Wärmebäder der Temperaturen ![]() und
und ![]() gekoppelt. Dabei soll
gekoppelt. Dabei soll
![]() gelten. Die Temperatur auf der Isothermen kann nur deshalb konstant
gehalten werden, da die Wärmebäder Wärme
gelten. Die Temperatur auf der Isothermen kann nur deshalb konstant
gehalten werden, da die Wärmebäder Wärme ![]() zuführen oder aufnehmen.
Die ausgetauschte Wärmemenge entlang einer Isothermen ist gegeben durch
zuführen oder aufnehmen.
Die ausgetauschte Wärmemenge entlang einer Isothermen ist gegeben durch
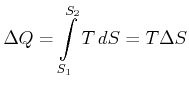 |
(4.375) |
| (4.376) |
Auf den Adiabaten ist die Änderung der inneren Energie proportional zu der
zugeführten mechanischen Arbeit. Da bei der Änderung von der Isothermen bei
![]() zu der bei
zu der bei ![]() die Änderung der inneren Energie das Negative der
Änderung beim Übergang von
die Änderung der inneren Energie das Negative der
Änderung beim Übergang von ![]() nach
nach ![]() sein. Deshalb tragen die Adiabaten
nichts zur abgegebenen mechanischen Arbeit bei.
sein. Deshalb tragen die Adiabaten
nichts zur abgegebenen mechanischen Arbeit bei.
Wir erhalten also für den Wirkungsgrad
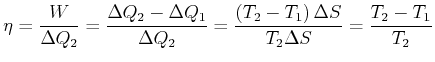 |
(4.377) |
Othmar Marti