Weiter: Der zweite Hauptsatz Oben: Wärmelehre Zurück: Wärmekraftmaschinen Skript: PDF-Datei Übungen: Blätter
| Dieser Stoff wurde am 04. 06. 2007 behandelt |
|
|
Materialien
Folien zur Vorlesung am 04. 06. 2007 PDF Übungsblatt 08 ausgegeben am 04. 06. 2007 Lösungsblatt 08 ausgegeben am 04. 06. 2007 |
Wärme ist Energie. Wenn Wärme transportiert wird, muss also Energie transportiert werden. Dies ist auf verschiedene Weise möglich:
Hier wollen wir Gleichungen für den Wärmetransport in Festkörpern angeben. Wenn die Festkörper Isolatoren sind, wird die Wärme durch Gitterschwingungen oder Phononen transportiert.
![\includegraphics[width=0.9\textwidth]{waermeleitung}](img1466.gif)
Mechanismus der
Wärmeleitung in Isolatoren. Die Kopplung lässt die Schwingung ausbreiten.
|
Wir nehmen an, dass bei gleichen Materialien der Wärmestrom zwischen zwei Punkten umso grösser ist, je grösser der Temperaturunterschied ist. In einer Dimension bedeutet dies, dass
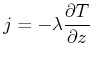 |
ist. In drei Dimensionen ersetzen wir wieder die Differentiation nach einer
Koordinate durch den Gradienten. Sei ![]() die Temperaturverteilung. Dann
ist die Wärmestromdichte in drei Dimensionen durch
die Temperaturverteilung. Dann
ist die Wärmestromdichte in drei Dimensionen durch
gegeben. Gleichung (4.100) heisst Wärmeleitungsgleichung.
![]() ist die Wärmeleitfähigkeit. Die Einheit der Wärmeleitfähigkeit ist
ist die Wärmeleitfähigkeit. Die Einheit der Wärmeleitfähigkeit ist
![$\displaystyle \left[\lambda\right] = \frac{W}{K m}$](img1470.gif) |
Die Einheit der Wärmestromdichte ![]() ist
ist
![$\displaystyle \left[j\right] = \frac{W}{m^{2}}$](img1473.gif) |
Der gesamte Wärmestrom ![]() ist die über eine Querschnittsfläche
ist die über eine Querschnittsfläche ![]() integrierte
Wärmestromdichte
integrierte
Wärmestromdichte ![]() .
.
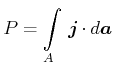 |
(4.379) |
![\includegraphics[width=0.9\textwidth]{waermeleitung_linear}](img1475.gif)
Wärmeleitung durch einen Stab
|
Wir betrachten die Wärmeleitung durch eine Prisma mit der Länge ![]() entlang
der Koordinatenachse
entlang
der Koordinatenachse ![]() . Das Prisma habe einem kleinen Querschnitt
. Das Prisma habe einem kleinen Querschnitt
![]() . Entlang des Stabes soll keine Energie verloren gehen. Im stationären
Zustand muss dann die Wärmestromdichte überall im Stab konstant sein.
. Entlang des Stabes soll keine Energie verloren gehen. Im stationären
Zustand muss dann die Wärmestromdichte überall im Stab konstant sein.
Die Temperatur soll sich über den Querschnitt (![]() - und
- und ![]() -Achse) nicht
ändern. Deshalb muss auch gelten
-Achse) nicht
ändern. Deshalb muss auch gelten
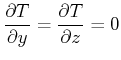 |
Aus der Wärmeleitungsgleichung (4.100) folgt dann
Analog zu der Strömung von Flüssigkeiten gibt es für Wärmeströme eine Kontinuitätsgleichung
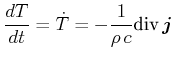 |
(4.383) |
wobei ![]() die Dichte des Materials ist (Einheit:
die Dichte des Materials ist (Einheit:
![]() ) und
) und ![]() die Wärmekapazität (Einheit:
die Wärmekapazität (Einheit:
![]() ).
).
Die Kontinuitätsgleichung besagt, dass die innere Energie und damit die Temperatur sich nur ändern können, wenn Wärme fliesst.
Die Wärmeleitungsgleichung und die Kontinuitätsgleichung für den Wärmestrom ergeben zusammen die Gleichung
Wenn Wärmequellen vorhanden sind, modifiziert sich die Kontinuumsgleichung zu
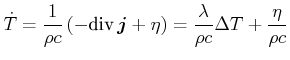 |
(4.386) |
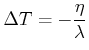 |
(4.387) |
![\includegraphics[width=0.7\textwidth]{waermeuebergang}](img1492.gif)
Wärmeübergang zwischen zwei Körpern
|
Die beiden Körper sollen sich an einer Kontaktfläche ganz nahe aneinander oder
in Kontakt gebracht werden. Diese Kontaktfläche habe die Grösse ![]() .
.
Die übertragene Wärmeleistung ist proportional zur Temperaturdifferenz.
Seien die ![]() die Wärmekapazitäten und
die Wärmekapazitäten und ![]() die Massen der beiden in Kontakt
gebrachten Körper
die Massen der beiden in Kontakt
gebrachten Körper ![]() und
und ![]() . Wenn die Temperatur des Körpers
. Wenn die Temperatur des Körpers ![]() konstant
ist, wenn
konstant
ist, wenn ![]() also ein Wärmereservoir oder Wärmebad ist (
also ein Wärmereservoir oder Wärmebad ist (
![]() , mit der
Wärmekapazität
, mit der
Wärmekapazität
![]() ) gilt
) gilt
| (4.388) |
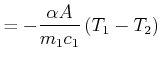 |
(4.389) |
Die Temperatur des Körpers ![]() mit der Masse
mit der Masse ![]() ändert sich also mit der
Zeit wie
ändert sich also mit der
Zeit wie
| (4.390) |
Wenn die Wärmeleitfähigkeit als konzentriertes Element behandelt werden kann, gelten bei komplizierten Netzwerken die Kirchhoffschen Gesetze.
![\includegraphics[width=0.7\textwidth]{gas-stoss-1}](img1507.gif)
Anzahl Moleküle, die
auf eine Fläche treffen.
|
Wir betrachten die Teilchen, nach dem letzten Zusammenstoss mit einem anderen
Molekül die Fläche ![]() durchqueren. Wir nehmen an, dass es keine Konvektion
gibt und dass das Gas an den Wänden deren Temperatur hat. Weiter sei
durchqueren. Wir nehmen an, dass es keine Konvektion
gibt und dass das Gas an den Wänden deren Temperatur hat. Weiter sei
![]() . Bei einer Fläche parallel zu den Platten an der Position
. Bei einer Fläche parallel zu den Platten an der Position ![]() gilt dann für die kinetischen Energien der Teilchen in den zwei möglichen
Richtungen
gilt dann für die kinetischen Energien der Teilchen in den zwei möglichen
Richtungen
![\includegraphics[width=0.4\textwidth]{gas-stoss-2}](img1513.gif)
Anzahl Atome auf einer Kugelfläche
|
Zur Berechnung der Wärmeleitung benötigen wir zuerst die Anzahl Atome auf einer Kugelfläche
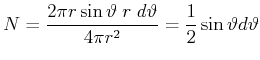 |
(4.391) |
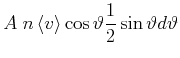 |
Die freie Flugstrecke ist dann proportional zur mittleren freien Weglänge
![]() . Wir setzen
. Wir setzen
![]() . An der Stelle des letzten
Zusammenstosses
. An der Stelle des letzten
Zusammenstosses
![]() berechnen wir die
Temperatur über das erste Glied der Taylor-Reihe
berechnen wir die
Temperatur über das erste Glied der Taylor-Reihe
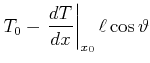 |
Die transportierte kinetische Energie ist
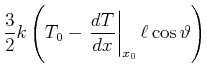 |
Insgesamt wird also
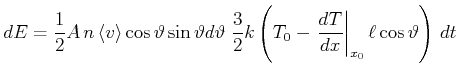 |
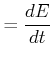 |
||
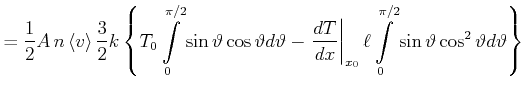 |
(4.392) |
Die beiden Teilintegrale ergeben
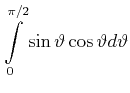 |
||
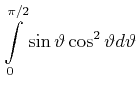 |
Also ist
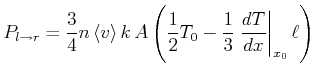 |
(4.393) |
und in der umgekehrten Richtung
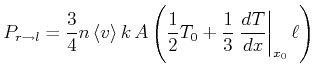 |
(4.394) |
In der Summe ist die Wärmeleistung
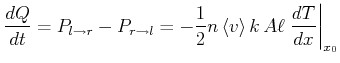 |
(4.395) |
Die Wärmeleitfähigkeit wird damit
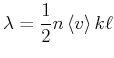 |
(4.396) |
Nun ist
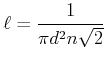 |
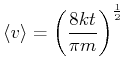 |
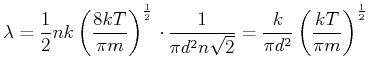 |
(4.397) |
unabhängig von ![]() und proportional zu
und proportional zu
![]() .
.
Wenn ![]() ist, bewegen sich die Moleküle von einer Wand zu der anderen
Wand, ohne dass sie sich untereinander stossen. Alle Moleküle, die von der Wand
ist, bewegen sich die Moleküle von einer Wand zu der anderen
Wand, ohne dass sie sich untereinander stossen. Alle Moleküle, die von der Wand
![]() streuen, haben eine Geschwindigkeitsverteilung, die der Temperatur
streuen, haben eine Geschwindigkeitsverteilung, die der Temperatur ![]() entspricht. Alle Moleküle, die von der Wand
entspricht. Alle Moleküle, die von der Wand ![]() streuen, haben eine
Geschwindigkeitsverteilung, die der Temperatur
streuen, haben eine
Geschwindigkeitsverteilung, die der Temperatur ![]() entspricht. Das Gas hat
somit keine thermische Verteilung und insbesondere keinen Temperaturgradienten.
entspricht. Das Gas hat
somit keine thermische Verteilung und insbesondere keinen Temperaturgradienten.
Die Wärmeleiteigenschaften von verdünnten Gasen werden zum Beispiel in Thermosflaschen oder Pirani-Vakuummessröhren verwendet.
Othmar Marti