Weiter: Anzahl Zustände und externe Oben: Wärmelehre Zurück: Wärmereservoire Skript: PDF-Datei Übungen: Blätter
(Siehe Reif, Statistical and Thermal Physics [Rei65, pp. 108])
Wir betrachten wieder zwei Systeme ![]() und
und ![]() im Kontakt.
im Kontakt. ![]() habe die Energie
habe die Energie ![]() ,
, ![]() die Energie
die Energie
![]() , wobei
, wobei ![]() die Energie des gesamten Systems
die Energie des gesamten Systems
![]() sein soll. Wir entwickeln die Energie
sein soll. Wir entwickeln die Energie ![]() um
ihren Maximalwert
um
ihren Maximalwert ![]() mit
mit
in eine Taylorreihe.
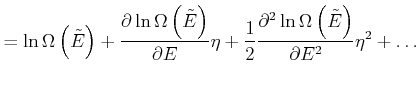 |
||
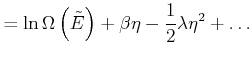 |
(4.435) |
Für das System ![]() gilt
gilt
und damit
| (4.437) |
Damit bekommen wir
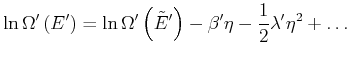 |
(4.438) |
Wir addieren die beiden Gleichungen und erhalten
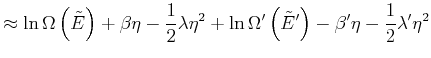 |
||
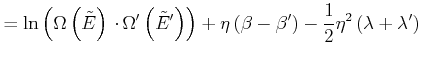 |
(4.439) |
Dies ist eine quadratische Funktion in ![]() . Damit diese ein Maximum hat, muss der Koeffizient von
. Damit diese ein Maximum hat, muss der Koeffizient von ![]() null
und der Koeffizient von
null
und der Koeffizient von ![]() negativ sein. Deshalb gilt beim Maximalwert von
negativ sein. Deshalb gilt beim Maximalwert von
![]() (Die beiden Teilsysteme sind unabhängig!)
(Die beiden Teilsysteme sind unabhängig!)
Dies bedeutet auch, dass die Temperaturen von ![]() und
und ![]() gleich sind.
gleich sind.
Wir setzen
![]() und können für die Wahrscheinlichkeiten
und können für die Wahrscheinlichkeiten
![]() schreiben:
schreiben:
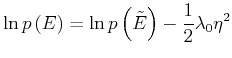 |
(4.440) |
oder
Die Grösse
![]() muss grösser null sein, da sonst
muss grösser null sein, da sonst ![]() kein Maximum hätte. Wenn wir
eines der beiden Teilsysteme sehr viel kleiner als das andere wählen, muss auch das
kein Maximum hätte. Wenn wir
eines der beiden Teilsysteme sehr viel kleiner als das andere wählen, muss auch das ![]() des grösseren
Systems grösser null sein. Deshalb gilt auch
des grösseren
Systems grösser null sein. Deshalb gilt auch
![]() und
und
![]()
Mit
![]() folgt
folgt
|
Aus Gleichung (4.164) folgt, dass |
Die mittlere Energie eines Systems ist also die Energie des Maximums der Gaussverteilung.
Die Gaussverteilung selber ist gegeben durch
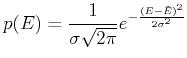 |
wobei ![]() die Standardabweichung ist. Der Vergleich mit Gleichung (4.164)
ergibt:
die Standardabweichung ist. Der Vergleich mit Gleichung (4.164)
ergibt:
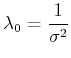 |
![\includegraphics[width=0.7\textwidth]{hauptsatz-zwei-009}](img1785.gif)
|
Weit ausserhalb des Maximums gilt
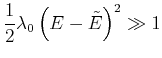 |
Dann ist
und
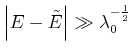 |
Die Breite der Verteilung,
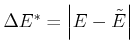 kann man dann
mit der Standardabweichung angeben, also
kann man dann
mit der Standardabweichung angeben, also
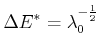 |
(4.443) |
Wir betrachten zwei Systeme ![]() und
und ![]() im Kontakt. Das gesamte System sei
im Kontakt. Das gesamte System sei
![]() . Wenn
. Wenn ![]() ist, dann ist ist
ist, dann ist ist
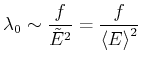 |
(4.444) |
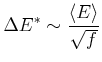 |
oder
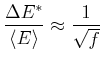 |
(4.445) |
Bei einem Mol Teilchen (
![]() ) ist die Breite der Verteilung
) ist die Breite der Verteilung
![]() .
.
Othmar Marti