Weiter: Eigenschaften der Entropie, dritter Oben: Wärmelehre Zurück: Wie breit ist das Skript: PDF-Datei Übungen: Blätter
(Siehe Reif, Statistical and Thermal Physics [Rei65, pp. 112])
Wir lassen nun einen externen Parameter ![]() zu.
zu. ![]() könnte zum Beispiel das
Volumen
könnte zum Beispiel das
Volumen ![]() sein. Die Anzahl Zustände
sein. Die Anzahl Zustände
![]() zwischen
zwischen
![]() und
und
![]() hängt nun von
hängt nun von ![]() ab. Sei
ab. Sei ![]() im Intervall
im Intervall
![]() .
.
Wenn ![]() sich um
sich um ![]() ändert, ändert sich die Energie des Mikrozustandes
ändert, ändert sich die Energie des Mikrozustandes
![]() um den Wert
um den Wert
![]() . Die
Änderung
. Die
Änderung
![]() ist für jeden Zustand anders.
ist für jeden Zustand anders.
Wir nennen
![]() ,
,![]() die Anzahl Zustände zwischen
die Anzahl Zustände zwischen ![]() und
und
![]() deren Ableitungen
deren Ableitungen
![]() zwischen
zwischen ![]() und
und
![]() liegen.
liegen.
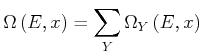 |
(4.446) |
Wenn wir ![]() um
um ![]() ändern, wie viele Zustände wechseln dann von einer Energie kleiner
ändern, wie viele Zustände wechseln dann von einer Energie kleiner ![]() zu einer Energie
grösser als
zu einer Energie
grösser als ![]() ?
?
Die Summe über alle Zustände ist
mit dem Mittelwert
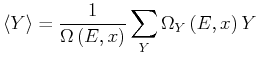 |
Wenn die Energie
eine Funktion von
![]() ist gilt für die Änderung der Energie des
Zustandes
ist gilt für die Änderung der Energie des
Zustandes ![]() .
.
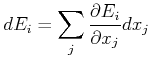 |
In der Physik heisst die Grösse
die zur Variablen |
| Dieser Stoff wurde am 21. 06. 2007 behandelt |
|
|
Materialien
Folien zur Vorlesung am 21. 06. 2007 PDF Übungsblatt 11 ausgegeben am 25. 06. 2007 |
Zum Beispiel gilt
![]() und damit
und damit
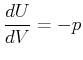 |
![]() ist also die zum Volumen konjugierte verallgemeinerte Kraft.
ist also die zum Volumen konjugierte verallgemeinerte Kraft.
Analog erhalten wir mit
![]() die Beziehung
die Beziehung
Die dazugehörige Arbeit
![]() ist allgemein so definiert (Gleichung für totale Differentiale):
ist allgemein so definiert (Gleichung für totale Differentiale):
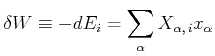 |
(4.450) |
|
Wie ändert sich nun
![]() wenn
wenn ![]() nach
nach
![]() ändert?
ändert? ![]() ist nach der
Definition in Gleichung (4.170) die Zahl der Moleküle von unterhalb
ist nach der
Definition in Gleichung (4.170) die Zahl der Moleküle von unterhalb ![]() nach oberhalb
nach oberhalb ![]() wechselt. Die
Grösse
wechselt. Die
Grösse
![]() nimmt zu, weil
nimmt zu, weil ![]() Zustände hinzukommen
und
Zustände hinzukommen
und
![]() Zustände wegfallen. Die Bilanz ist (wir verwenden die Definition der Ableitung)
Zustände wegfallen. Die Bilanz ist (wir verwenden die Definition der Ableitung)
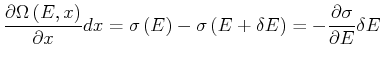 |
(4.451) |
Aus Gleichung (4.171) bekommt man
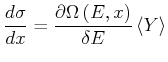 |
und damit
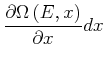 |
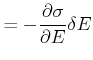 |
|
![$\displaystyle = -\frac{\partial}{\partial E}\left[\frac {\Omega\left( E\text{,} x\right) }{\delta E}\left<Y\right>dx\right]\delta E$](img1834.gif) |
||
![$\displaystyle =-\frac{\partial}{\partial E}\left[ {\Omega\left( E\text{,} x\right) }\left<Y\right>\right]dx$](img1835.gif) |
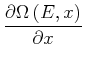 |
![$\displaystyle = -\frac{\partial}{\partial E}\left[ {\Omega\left( E\text{,} x\right) }\left<Y\right>\right]$](img1837.gif) |
|
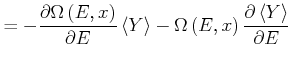 |
Wir teilen beide Seiten durch
![]() und bekommen
und bekommen
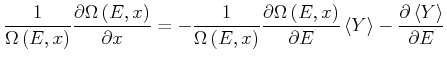 |
Diese Gleichung ist äquivalent zu
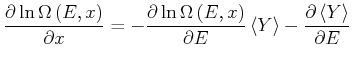 |
(4.452) |
Wenn
![]() ist, ist der erste Summand
ist, ist der erste Summand
![]() . Den zweiten Summanden kann man abschätzen, wenn man die Ableitung
. Den zweiten Summanden kann man abschätzen, wenn man die Ableitung
![]() durch die Steigung der Gerade zum Nullpunkt
durch die Steigung der Gerade zum Nullpunkt
![]() ersetzt. Dann
ist der erste Summand auf der rechten Seite der Gleichung für grosse Systeme (
ersetzt. Dann
ist der erste Summand auf der rechten Seite der Gleichung für grosse Systeme (![]() ) um den Faktor
) um den Faktor ![]() grösser als der zweite Summand. Der zweite Summand
grösser als der zweite Summand. Der zweite Summand
![]() kann deshalb
vernachlässigt werden. Mit
kann deshalb
vernachlässigt werden. Mit
![]() und Gleichung (4.172) bekommt man
und Gleichung (4.172) bekommt man
Diese formale Beziehung soll nun anhand von Beispielen erläutert werden.
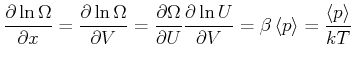 |
(4.454) |
Bei mehreren externen Parametern modifiziert sich Gleichung (4.176) zu
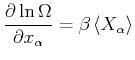 |
Wir betrachten ein isoliertes System
![]() , das aus zwei Teilsystemen besteht. Das Volumen
, das aus zwei Teilsystemen besteht. Das Volumen ![]() ist vom
Volumen
ist vom
Volumen ![]() durch einen beweglichen Kolben getrennt. Die Gesamtenergie sei konstant:
durch einen beweglichen Kolben getrennt. Die Gesamtenergie sei konstant:
![]() , wie auch
das Gesamtvolumen
, wie auch
das Gesamtvolumen
![]() . Die beiden Systeme tauschen Wärme und mechanische Arbeit aus.
. Die beiden Systeme tauschen Wärme und mechanische Arbeit aus.
![\includegraphics[width=0.5\textwidth]{hauptsatz-zwei-010}](img1857.gif)
Skizze
eines gekoppelten Systems, das durch einen Kolben getrennt ist.
|
Wir betrachten eine infinitesimale Änderung des Zustandes mit den externen
Parametern ![]() und verwenden Gleichung (4.176) (verallgemeinerte Kräfte)
und verwenden Gleichung (4.176) (verallgemeinerte Kräfte)
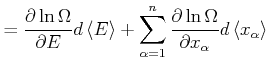 |
||
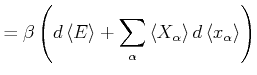 |
(4.455) |
In unserem Falle ist
![]() und
und ![]() die innere Energie. Somit
erhalten wir mit
die innere Energie. Somit
erhalten wir mit
![]() für unseren infinitesimalen Prozess
für unseren infinitesimalen Prozess
| (4.456) |
Wir können für infinitesimale Prozesse auch schreiben
| (4.457) |
Bei einem adiabatischen Prozess ist
![]() und damit
und damit ![]() . Somit ändert
sich auch
. Somit ändert
sich auch ![]() bei einem adiabatischen Prozess nicht!
bei einem adiabatischen Prozess nicht!
Das Gleichgewicht ist erreicht, wenn die Wahrscheinlichkeit
ist.
Die Anzahl Zustände des Gesamtsystems sind
| (4.458) |
Das Maximum der Wahrscheinlichkeit, der Anzahl Zustände ![]() und damit der
Entropie
und damit der
Entropie ![]() wird erreicht, wenn
wird erreicht, wenn
| (4.459) |
Analog erhält man für das zweite Teilsystem ![]()
Wir haben dabei wegen der Energieerhaltung ![]() und wegen der
Volumenerhaltung
und wegen der
Volumenerhaltung ![]() geschrieben. Die Summe der Gleichungen
4.184 und 4.185 ergibt
geschrieben. Die Summe der Gleichungen
4.184 und 4.185 ergibt
| (4.462) |
Dies muss für beliebige ![]() und
und ![]() gelten. Darum haben wir
gelten. Darum haben wir
| (4.463) | ||||||||||
| (4.464) |
Dies sind die erwarteten Gleichgewichtsbedingungen, aber nun mit statistischen Argumenten hergeleitet.
Othmar Marti