Weiter: Anwendung auf das ideale Oben: Wärmelehre Zurück: Anzahl Zustände und externe Skript: PDF-Datei Übungen: Blätter
In diesem Abschnitt wollen wir die Eigenschaften der Entropie untersuchen. Wir betrachten dazu zwei Makrozustände
![]() (initial) und
(initial) und ![]() (final). Für die Entropieänderung erhalten wir allgemein
(final). Für die Entropieänderung erhalten wir allgemein
![\includegraphics[width=0.4\textwidth]{entropie_messung}](img1893.gif)
Skizze einer Apparatur zur Messung der Entropie. Mit
dem Widerstand
|
Gleichung (4.189) zeigt, wie Entropiedifferenzen gemessen werden können. Wir nehmen an, dass sich das System im
Gleichgewicht bei der Temperatur ![]() befindet. Nun wird mit dem Widerstand die Wärmemenge
befindet. Nun wird mit dem Widerstand die Wärmemenge
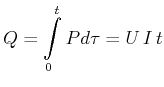 |
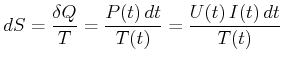 |
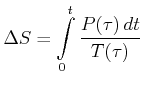 |
(4.466) |
![\includegraphics[width=0.48\textwidth]{hauptsatz_drei-002}](img1899.gif)
![\includegraphics[width=0.48\textwidth]{hauptsatz_drei-003}](img1900.gif)
Links ist
|
![\includegraphics[width=0.48\textwidth]{hauptsatz_drei-006}](img1904.gif)
![\includegraphics[width=0.48\textwidth]{hauptsatz_drei-007}](img1905.gif)
Links ist
|
![\includegraphics[width=0.48\textwidth]{hauptsatz_drei-008}](img1906.gif)
![\includegraphics[width=0.48\textwidth]{hauptsatz_drei-009}](img1907.gif)
Links ist
|
Da die Entropie als
![]() geschrieben werden kann, hängt die Entropie eindeutig vom Makrozustand des
Systems ab, wenn wir das Phasenraumvolumen auf
geschrieben werden kann, hängt die Entropie eindeutig vom Makrozustand des
Systems ab, wenn wir das Phasenraumvolumen auf
![]() fixieren. Bei einer klassischen Betrachtung würde
gelten
fixieren. Bei einer klassischen Betrachtung würde
gelten
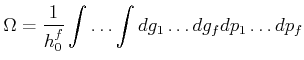 |
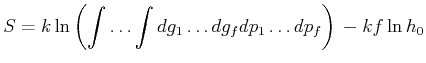 |
Wir nehmen nun an, dass der niedrigste mögliche Energiegehalt eines Systems ![]() sei. Diese niedrigste Energie
entspricht der Nullpunktsenergie in der Quantenmechanik. Für die folgende Betrachtung ist nicht wichtig, woher
sei. Diese niedrigste Energie
entspricht der Nullpunktsenergie in der Quantenmechanik. Für die folgende Betrachtung ist nicht wichtig, woher
![]() rührt, sondern dass sie existiert. Für
rührt, sondern dass sie existiert. Für
![]() gilt
gilt
| (4.467) |
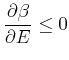 |
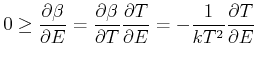 |
| (4.469) |
|
3. Hauptsatz (strenge Form)
Wenn Max Planck |
Es gibt nun Systeme (zum Beispiel Gläser), die bei ![]() in metastabile Zustände mit praktisch unendlicher
Lebensdauer geraten. Diese metastabilen Systeme sind nicht im Grundzustand, deshalb ist
in metastabile Zustände mit praktisch unendlicher
Lebensdauer geraten. Diese metastabilen Systeme sind nicht im Grundzustand, deshalb ist
![]() .
.
|
3. Hauptsatz (engere Form)
Für |
Die Wärmekapazitäten von Stoffen hängen mit der Entropie zusammen. Aus
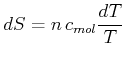 |
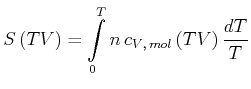 |
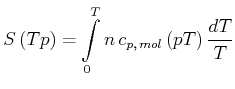 |
| (4.470) |
| Dieser Stoff wurde am 25. 06. 2007 behandelt |
|
|
Materialien
Folien zur Vorlesung am 25. 06. 2007 PDF |
Wir hatten früher den Wirkungsgrad von Wärmekraftmaschinen abgeleitet:
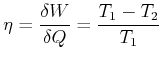 für für |
(4.471) |
Analog gilt für Kältemaschinen:
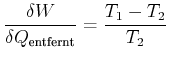 |
(4.472) |
Kann man den Temperaturnullpunkt mit einer Kältemaschine erreichen? Für
![]() gilt
gilt
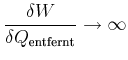 |
Das heisst, es muss immer mehr mechanische Energie in ein System gesteckt werden, um die Temperatur weiter zu erniedrigen. Da diese Energie divergiert, muss
| Mit einer Kältemaschine ist der absolute Temperaturnullpunkt nicht erreichbar. |
Dies ist eine alternative Fassung des dritten Hauptsatzes.
Bemerkung:
Es gilt auch
Othmar Marti