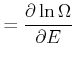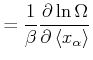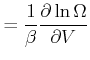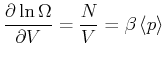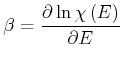Anwendung auf das ideale Gas

Die folgenden Beziehungen gelten:

$$\beta =\frac{\partial\ln\Omega}{\partial E}$$

$$\left<x_{\alpha}\right> =\frac{1}{\beta}\frac{\partial\ln\Omega}{\partial\left<x_{\alpha}\right>}$$

$$\left<p\right> =\frac{1}{\beta}\frac{\partial\ln\Omega}{\partial V}$$

$$\Omega \propto V^{N} \chi\left( E\right)$$

Wenn wir die Beziehung für 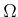$\Omega$ logarithmieren, erhalten wir

$$\ln\Omega=N\ln V+\ln\chi\left( E\right) +const$$

Daraus erhalten wir die Ableitung nach dem Volumen

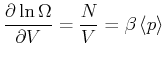$$\frac{\partial\ln\Omega}{\partial V}=\frac{N}{V}=\beta\left<p\right>$$ (4.473)

Wir können also für den gemittelten Druck 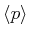$\left<p\right>$ schreiben

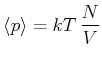$$\left<p\right>= kT \frac{N}{V}$$ (4.474)

Umgestellt erkennen wir in Gleichung (4.198) die ideale Gasgleichung

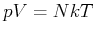$$pV=NkT$$ (4.475)

Wir haben also gezeigt, dass die ideale Gasgleichung aus der Statistik für unkorrelierte Teilchen folgt. Weiter besteht die Beziehung

$$\beta =\frac{\partial\ln\chi\left( E\right) }{\partial E}$$

Es folgt daraus, dass für ein ideales Gas die Energie 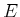$E$ nur von 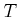$T$ abhängen kann.

$$E=E\left( T\right)$$