Weiter: Anwendung auf das van-der-Waals-Gas Oben: Wärmelehre Zurück: Maxwellrelationen für homogene Substanzen Skript: PDF-Datei Übungen: Blätter
Wir suchen einen Zusammenhang für ![]() und
und ![]() für beliebige Substanzen und beliebige Zustandsdichten
für beliebige Substanzen und beliebige Zustandsdichten
![]() . Wir kennen für höhere Temperaturen und ideale Gase den Zusammenhang der molaren Grössen
. Wir kennen für höhere Temperaturen und ideale Gase den Zusammenhang der molaren Grössen
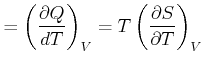 |
||
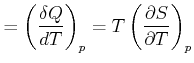 |
(4.536) |
Die Entropie soll
![]() vom Druck und der Temperatur abhängen. Dann gilt für die ausgetauschte
Wärmemenge
vom Druck und der Temperatur abhängen. Dann gilt für die ausgetauschte
Wärmemenge
![$\displaystyle \delta Q=TdS=T\left[ \left( \frac{\partial S}{\partial p}\right) _{T}dp+\left( \frac{\partial S}{\partial T}\right)_{p}dT\right]$](img2170.gif) |
(4.537) |
Wir setzen die Definition von ![]() ein und erhalten
ein und erhalten
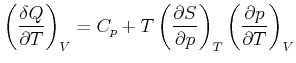 |
(4.539) |
Zur weiteren Berechnung drücken wir ![]() als Funktion von
als Funktion von ![]() aus
aus
Da wir ![]() suchen, ist das Volumen konstant, der zweite Summand in Gleichung (4.268) ,
suchen, ist das Volumen konstant, der zweite Summand in Gleichung (4.268) ,
![]() , ist gleich null. Wir erhalten also für
, ist gleich null. Wir erhalten also für ![]()
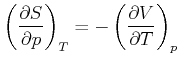 |
Wir ersetzen nun die beiden partiellen Ableitungen durch den Volumenausdehnungskoeffizienten ![]() und die
isotherme Kompressibilität
und die
isotherme Kompressibilität ![]() . Die Definition des Volumenausdehnungskoeffizienten lautet
. Die Definition des Volumenausdehnungskoeffizienten lautet
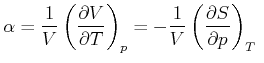 |
(4.543) |
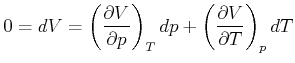 |
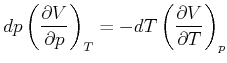 |
Mit der Definition der isothermen Kompressibilität
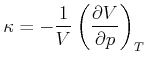 |
(4.545) |
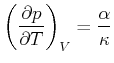 |
(4.546) |
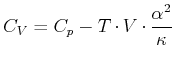 |
(4.547) |
Für molare Wärmekapazitäten erhalten wir die Beziehung
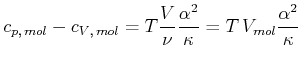 |
(4.549) |
Die spezifischen Wärmekapazitäten
![]() hängen wie folgt zusammen:
hängen wie folgt zusammen:
Beispiel:
Für Kupfer erhalten wir die folgenden Beziehungen
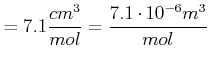 |
||
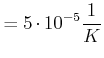 |
||
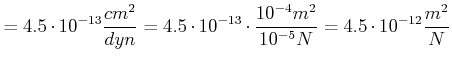 |
||
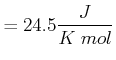 |
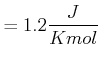 |
||
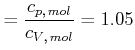 |
| Dieser Stoff wurde am 05. 07. 2007 behandelt |
|
|
Materialien
Folien zur Vorlesung am 05. 07. 2007 PDF Übungsblatt 13 ausgegeben am 09. 07. 2007 Lösungsblatt 13 ausgegeben am 09. 07. 2007 |
Hier wollen wir untersuchen, wie ![]() sich mit dem Volumen ändert. Die Wärmekapazität
sich mit dem Volumen ändert. Die Wärmekapazität
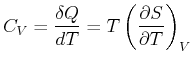 |
Die Volumenableitung der Wärmekapazität ist
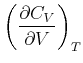 |
![$\displaystyle =\left( \frac{\partial}{\partial V}\right) _{T}\left[ T\left( \frac{\partial S}{\partial T}\right) _{V}\right]$](img2212.gif) |
|
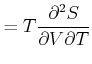 |
||
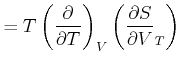 |
||
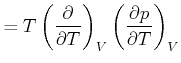 |
(4.552) |
Mit der Zustandsgleichung für das ideale Gas ![]() erhält man
erhält man
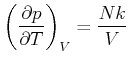 |
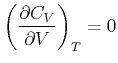 |
Hier möchten wir wissen, wie die innere Energie ![]() von der Temperatur und dem Volumen abhängt? Wir verwenden
Gleichung (4.279) und erhalten
von der Temperatur und dem Volumen abhängt? Wir verwenden
Gleichung (4.279) und erhalten
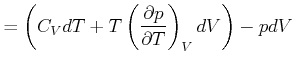 |
||
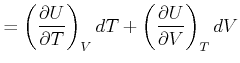 |
(4.554) |
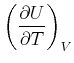 |
(4.555) | |
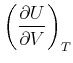 |
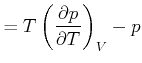 |
(4.556) |
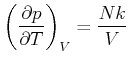 |
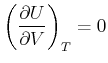 |
Othmar Marti