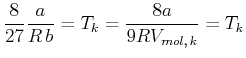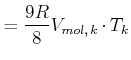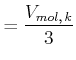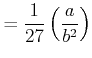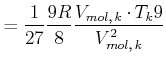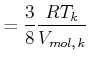Unterabschnitte
(Siehe Gerthsen, Physik [Mes06, pp. 269])
In diesem Abschnitt sollen die Eigenschaften des van-der-Waals-Gases berechnet werden.
- Die Teilchen im van-der-Waals-Gas haben ein Eigenvolumen. Sie sind nicht punktförmig.
- Zwischen den Teilchen existieren anziehende Kräfte.
Die Berechnung der Zustandsfunktion des van-der-Waals-Gases startet mit der Gleichung für den Druck des Gases auf
die Wand
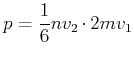 |
(4.557) |
Diese Gleichung wurde in einem vorherigen Kapitel abgeleitet. Wir hatten dabei nicht zwischen den
Geschwindigkeiten 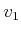 und
und 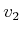 unterschieden. Die beiden Geschwindigkeiten sind:
unterschieden. Die beiden Geschwindigkeiten sind:
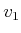
- Auftreffgeschwindigkeit der Teilchen auf die Wand
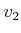
- Ausbreitungsgeschwindigkeit des Impulses
Wenn nun 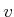 die mittlere Geschwindigkeit der Moleküle ist, gelten die Beziehungen
die mittlere Geschwindigkeit der Moleküle ist, gelten die Beziehungen
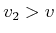 . Da die Teilchen ein Volumen haben, springt der Impuls bei jedem Stoss um
. Da die Teilchen ein Volumen haben, springt der Impuls bei jedem Stoss um 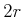 weiter, wobei
weiter, wobei
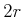 der Durchmesser eines Moleküls ist.
der Durchmesser eines Moleküls ist.
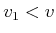 . Die gegenseitigen Anziehungskräfte der Moleküle wirken wie die Oberflächenspannung bei
Flüssigkeiten. Dadurch werden die Moleküle abgebremst, bevor sie am Rande des Gases mit der Wand
zusammenstossen.
. Die gegenseitigen Anziehungskräfte der Moleküle wirken wie die Oberflächenspannung bei
Flüssigkeiten. Dadurch werden die Moleküle abgebremst, bevor sie am Rande des Gases mit der Wand
zusammenstossen.
Bei jedem Stoss wird der Impuls um 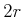 weiter als die mittlere
freie Weglänge weiter als die mittlere
freie Weglänge 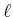 bewegt. bewegt.
|
Aus der Abbildung 4.50 entnehmen wir, dass bei einer mittleren freien Weglänge 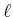 zwischen
zwei Stössen der Impuls sich jeweils um
zwischen
zwei Stössen der Impuls sich jeweils um
weiter bewegt. Die Geschwindigkeit der Impulsausbreitung ist also
Andererseits ist die mittlere freie Weglänge durch
gegeben, wobei der Durchmesser der Streuquerschnittsfläche 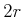 beträgt. Damit wird
beträgt. Damit wird
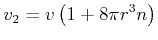 |
(4.558) |
Die einzelnen Moleküle werden als Kugeln mit einem Radius 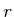 modelliert. Ihr Volumen ist dann
modelliert. Ihr Volumen ist dann
Damit hängt 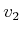 vom Molekülvolumen ab!
vom Molekülvolumen ab!
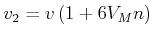 |
(4.559) |
Der Impuls breitet sich nur dann mit der berechnteten Geschwindigkeit 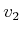 aus, wenn wir zentrale lineare Stösse
betrachten. Wenn wir schiefe Stösse berücksichtigen, erhalten wir
aus, wenn wir zentrale lineare Stösse
betrachten. Wenn wir schiefe Stösse berücksichtigen, erhalten wir
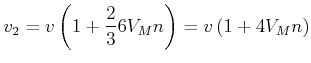 |
(4.560) |
Der Faktor 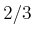 stammt von der Mittelung über den ganzen Stossquerschnitt (Siehe Anhang
I!) Das gemittelte Resultat aus Gleichung (I.2) ist
stammt von der Mittelung über den ganzen Stossquerschnitt (Siehe Anhang
I!) Das gemittelte Resultat aus Gleichung (I.2) ist
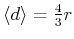 . Wir
hatten mit
. Wir
hatten mit 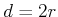 gerechnet. Der Quotient aus beiden ergibt den Korrekturfaktor
gerechnet. Der Quotient aus beiden ergibt den Korrekturfaktor 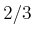 .
.
Wie bei der Oberflächenspannung von Flüssiggkeiten heben sich die Anziehungskräfte an der Grenzfläche zur Wand
nicht auf. Es existiert eine nach innen gerichtete Kraft
die proportional zur Teilchzenzahldichte 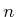 und einem hier nicht berechneten Faktor
und einem hier nicht berechneten Faktor 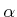 ist. Aus dieser
Kraft resultiert die Impulsänderung
ist. Aus dieser
Kraft resultiert die Impulsänderung 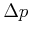
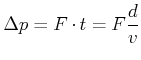 |
(4.561) |
bei der Annäherung an die Wand, wobei 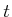 die Stosszeit und
die Stosszeit und 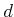 die Distanz zur zur Wand ist.
die Distanz zur zur Wand ist. 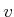 ist die mittlere
Geschwindigkeit der Moleküle. Beim Auftreffen an die Wand haben die Moleküle im Mittel die Geschwindigkeit
ist die mittlere
Geschwindigkeit der Moleküle. Beim Auftreffen an die Wand haben die Moleküle im Mittel die Geschwindigkeit 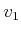
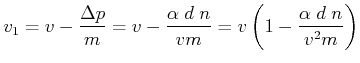 |
(4.562) |
Setzen wir nun 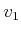 und
und 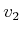 in die Gleichung (4.285) ein, so erhalten wir
in die Gleichung (4.285) ein, so erhalten wir
Wir betrachten nun im Folgenden ein Mol Gas. Die Teilchenzahldichte ist dann
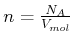 .
Gleichung (4.291) wird dann
.
Gleichung (4.291) wird dann
wobei wir die Beziehung
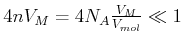 verwendet haben. Dies impliziert, dass wir
verdünnte Gase betrachten.
verwendet haben. Dies impliziert, dass wir
verdünnte Gase betrachten.
Die kinetische Energie eines Mols dieses Gases liefert die Beziehung
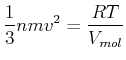 |
(4.565) |
Wir definieren nun die beiden Koeffizienten 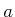 (beschreibt den Binnendruck) und
(beschreibt den Binnendruck) und 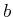 (das vierfache
Eigenvolumen der Moleküle, auch Kovolumen genannt.) durch
(das vierfache
Eigenvolumen der Moleküle, auch Kovolumen genannt.) durch
Mit diesen Definitionen wird Gleichung (4.292)
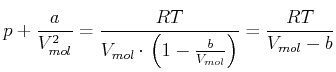 |
(4.568) |
Umgestellt erhalten wir die molare van-der-Waals-Gleichung
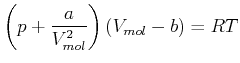 |
(4.569) |
|
Beispiel:
Für 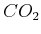 sind die beiden Parameter
sind die beiden Parameter
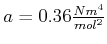 und
und
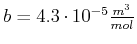 .
.
Isothermen von 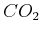
|
Das 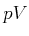 -Diagramm eines van-der-Waals-Gases ist bei unabhängigem
-Diagramm eines van-der-Waals-Gases ist bei unabhängigem 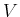 eindeutig. Betrachtet man
eindeutig. Betrachtet man 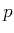 als unabhängige
Variable, ist die Funktion nicht eindeutig. Zu einem Druck kann es drei verschiedene Volumina geben.
als unabhängige
Variable, ist die Funktion nicht eindeutig. Zu einem Druck kann es drei verschiedene Volumina geben.
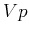 -Diagramm -Diagramm
|
Dies bedeutet, dass es zu einem Druck eine dichte Phase und eine verdünnte Phase gibt. Die dichtere Phase nennen
wir Flüssigkeit, die verdünnte Phase Gas. Das van-der-Waals-Modell sagt also, dass es einen
Phasenübergang gibt.
Die Maxwellsche Konstruktion erlaubt, im Bereich der Mehrdeutigkeit den Zustand des Systems festzulegen.
Komprimieren wir das System entlang der Isotherme, so wird bei 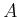 die Kurve verlassen. Das System bewegt sich
entlang
die Kurve verlassen. Das System bewegt sich
entlang 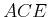 , wobei Flüssigkeit und Gas im Gleichgewicht sind. Danach folgt das System der Isotherme. Entlang der
horizontalen Gerade
, wobei Flüssigkeit und Gas im Gleichgewicht sind. Danach folgt das System der Isotherme. Entlang der
horizontalen Gerade 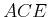 haben wir eine Koexistenz flüssig-gasförmig. Das Volumenverhältnis zwischen Flüssigkeit
und Gas wird über das Hebelgesetz berechnet. Am Punkt
haben wir eine Koexistenz flüssig-gasförmig. Das Volumenverhältnis zwischen Flüssigkeit
und Gas wird über das Hebelgesetz berechnet. Am Punkt 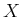 ist der Anteil der Flüssigkeit
ist der Anteil der Flüssigkeit
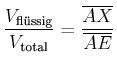 |
(4.570) |
Der Gasanteil ist
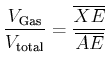 |
(4.571) |
Die Lage der Gerade wird so festgelegt, dass die Flächen zwischen der Geraden und der Isotherme oberhalb und
unterhalb gleich sind.
Eine Fläche im 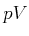 -Diagramm hat die Einheit der Energie. Die Maxwellsche Konstruktion ist also ein Rezept, wie
das Energiegleichgewicht gefunden werden kann.
-Diagramm hat die Einheit der Energie. Die Maxwellsche Konstruktion ist also ein Rezept, wie
das Energiegleichgewicht gefunden werden kann.
Gibt es keine Kondensationskeime in dem System, ist das System also absolut rein, kann keine Flüssigkeit
entstehen. Die Flüssigkeit kondensiert nicht. Die Wände des Gefässes können natürlich auch als Kondensationskeime
dienen. Die Zustände entlang der Isotherme bedeuten:
- AB
- Hier ist der Dampf übersättigt. Das System kann sich nur entlang
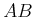 bewegen, wenn Kondensationskeime
fehlen. In der Nebelkammer wird dies ausgenutzt. Elektronen oder sonstige Teilchen dienen als
Kondensationskeime. Die Nebelspur macht sie sichtbar.
bewegen, wenn Kondensationskeime
fehlen. In der Nebelkammer wird dies ausgenutzt. Elektronen oder sonstige Teilchen dienen als
Kondensationskeime. Die Nebelspur macht sie sichtbar.
- DE
- Hier haben wir eine überhitzte Flüssigkeit, die ohne Kondensationskeime nicht gasförmig werden kann.
Wird Wasser in einer Mikrowelle erhitzt, so erhält man in der Regel eine überhitzte Flüssigkeit, die durch
Schütteln beim Herausnehmen schlagartig verdampfen wird und so schwere Verletzungen hervorrufen kann.
Bemerkung:
Beim van-der-Waals-Gas ist bei tiefen Temperaturen
Zur Berechnung der Lage der beiden Extremalpunkte 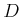 und
und 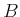 betrachten wir die Funktion
betrachten wir die Funktion
Die Extremalpunkte sind durch
gegeben. Setzen wir 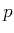 aus Gleichung (4.297) ein, erhalten wir
aus Gleichung (4.297) ein, erhalten wir
Die Extremwerte sind durch
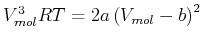 |
(4.572) |
Für hohe Temperaturen gibt es keine Maxima und Minima (Siehe Abbildung 4.51). Bei der Isotherme mit der
höchsten Temperatur, bei der die ersten Extrema erscheinen, fallen das Maximum und das Minimum zusammen. Dieser
Punkt heistkritischer Punkt mit dem kritischen Druck 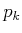 und dem kritischen Molvolumen
und dem kritischen Molvolumen
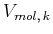 . Es existiert nur eine solche Isotherme
. Es existiert nur eine solche Isotherme 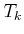 . Dann gilt
. Dann gilt
Wir erhalten
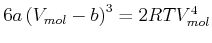 |
(4.573) |
Wir teilen nun Gleichung (4.301) durch Gleichung (4.300) , so erhalten wir
Das kritische Molvolumen
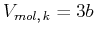 |
(4.574) |
Setzen wir Gleichung (4.302) in Gleichung (4.300) ein, erhalten wir die kritische Temperatur
und damit
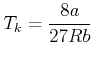 |
(4.575) |
Schliesslich können wir den kritischen Druck berechnen.
Damit ist der kritische Druck
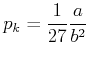 |
(4.576) |
Beispiel:
Mit den Werten für 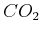 (
(
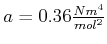 und
und
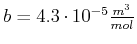 ) bekommen wir
) bekommen wir
Amagat-Diagramm oder 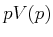 -Diagramm. Dieses Diagramm
zeigt besonders schön die Abweichung vom Verhalten des idealen Gases. Beim Idealen Gas wäre -Diagramm. Dieses Diagramm
zeigt besonders schön die Abweichung vom Verhalten des idealen Gases. Beim Idealen Gas wäre 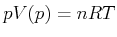 eine von
der Temperatur abhängige Gerade. eine von
der Temperatur abhängige Gerade.
|
| Dieser Stoff wurde am 09. 07. 2007
behandelt |
![\includegraphics[height=8mm]{icon-mat}](img40.gif) |
Materialien
Folien zur Vorlesung am 09. 07. 2007 PDF
|
Mit Hilfe des kritischen Punktes kann die van-der-Waals-Gleichung (4.297) umgeschrieben werden. Wir setzen
und erhalten
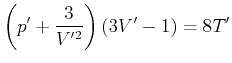 |
(4.577) |
Weiter können wir 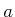 und
und 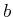 mit den Koordinaten des kritischen Punktes ausdrücken.
mit den Koordinaten des kritischen Punktes ausdrücken.
Daraus erhalten wir
Schliesslich bekommen wir
Othmar Marti
Experimentelle Physik
Universiät Ulm
![]() die mittlere Geschwindigkeit der Moleküle ist, gelten die Beziehungen
die mittlere Geschwindigkeit der Moleküle ist, gelten die Beziehungen
![\includegraphics[width=0.7\textwidth]{thermodynamik-001}](img2234.gif)
![]() zwischen
zwei Stössen der Impuls sich jeweils um
zwischen
zwei Stössen der Impuls sich jeweils um
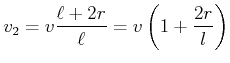
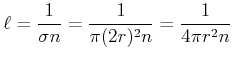
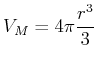
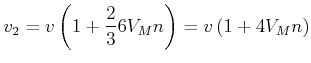
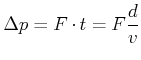
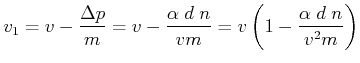
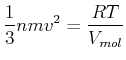
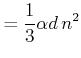
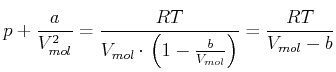
![]() sind die beiden Parameter
sind die beiden Parameter
![]() und
und
![]() .
.
![\includegraphics[width=0.7\textwidth]{thermodynamik-003}](img2267.gif)
![]() -Diagramm eines van-der-Waals-Gases ist bei unabhängigem
-Diagramm eines van-der-Waals-Gases ist bei unabhängigem ![]() eindeutig. Betrachtet man
eindeutig. Betrachtet man ![]() als unabhängige
Variable, ist die Funktion nicht eindeutig. Zu einem Druck kann es drei verschiedene Volumina geben.
als unabhängige
Variable, ist die Funktion nicht eindeutig. Zu einem Druck kann es drei verschiedene Volumina geben.
![\includegraphics[width=0.5\textwidth]{thermodynamik-004}](img2268.gif)
![\includegraphics[width=0.5\textwidth]{thermodynamik-005}](img2269.gif)
![]() die Kurve verlassen. Das System bewegt sich
entlang
die Kurve verlassen. Das System bewegt sich
entlang ![]() , wobei Flüssigkeit und Gas im Gleichgewicht sind. Danach folgt das System der Isotherme. Entlang der
horizontalen Gerade
, wobei Flüssigkeit und Gas im Gleichgewicht sind. Danach folgt das System der Isotherme. Entlang der
horizontalen Gerade ![]() haben wir eine Koexistenz flüssig-gasförmig. Das Volumenverhältnis zwischen Flüssigkeit
und Gas wird über das Hebelgesetz berechnet. Am Punkt
haben wir eine Koexistenz flüssig-gasförmig. Das Volumenverhältnis zwischen Flüssigkeit
und Gas wird über das Hebelgesetz berechnet. Am Punkt ![]() ist der Anteil der Flüssigkeit
ist der Anteil der Flüssigkeit
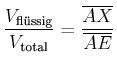
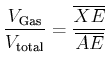
![]() und
und ![]() betrachten wir die Funktion
betrachten wir die Funktion
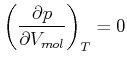
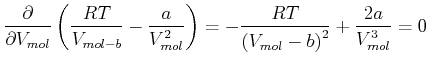
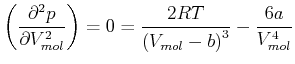
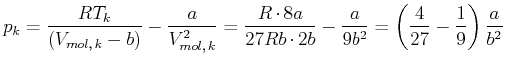
![]() (
(
![]() und
und
![]() ) bekommen wir
) bekommen wir
![\includegraphics[width=0.7\textwidth]{thermodynamik-006}](img2298.gif)
![]() und
und ![]() mit den Koordinaten des kritischen Punktes ausdrücken.
mit den Koordinaten des kritischen Punktes ausdrücken.