Weiter: Mehrstoffsysteme, Lösungen Oben: Wärmelehre Zurück: Joule-Thomson-Effekt Skript: PDF-Datei Übungen: Blätter
Aus der Gleichung für das van der Waals-Gas folgt, dass es einen Koexistenzbereich von Flüssigkeit und Gas gibt.
Wenn die Moleküle sich wie ein Gas verhalten, ist dies der gasförmige Aggregatszustand. Die van der Waals-Gleichung gibt eine makroskopische Erklärung der Phasen. Wie könnte eine mikroskopische Erklärung aussehen?
![\includegraphics[width=0.7\textwidth]{aggregatszustaende-001}](img2432.gif)
Oberflächenspannung und potentielle Energie
|
Die Oberflächenspannung bewirkt eine von der Oberfläche nach innen gerichtete Kraft, die dann zu einer potentiellen Energie führt
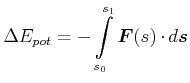
Welche Moleküle haben genügend Energie ![]() zum Verlassen der Flüssigkeit? Um diese Frage zu beantworten, muss die
Energieverteilung der Moleküle in der Flüssigkeit betrachtet werden. Die hohen Energien sind auf jeden Fall
Boltzmann-verteilt.
zum Verlassen der Flüssigkeit? Um diese Frage zu beantworten, muss die
Energieverteilung der Moleküle in der Flüssigkeit betrachtet werden. Die hohen Energien sind auf jeden Fall
Boltzmann-verteilt.
| (4.621) |
Diese Gleichung beschreibt den Dampfdruck ![]() .
. ![]() ist die
Verdampfungsenergie pro Molekül.
ist die
Verdampfungsenergie pro Molekül.
![\includegraphics[width=0.7\textwidth]{h2o}](img2436.gif)
|
In diesem Diagramm gibt es zwei ausgezeichnete Temperaturen, den kritischen
Punkt mit der kritischen Temperatur ![]() und den Tripelpunkt mit der
Temperatur
und den Tripelpunkt mit der
Temperatur ![]() .
.
Bemerkung:
Die Existenz des kritischen Punktes kann verwendet werden, um fragile Objekte durch Umrunden von ![]() aus der
Flüssigkeit zu entfernt. Auf diese Weise wird Flüssigkeit zu Gas, ohne zu verdampfen.
aus der
Flüssigkeit zu entfernt. Auf diese Weise wird Flüssigkeit zu Gas, ohne zu verdampfen.
Um die Steigung der Dampfdruckkurve zu verstehen, betrachten wir eine Carnot-Maschine, di mit einer verdampfenden (oder kondensierenden ) Flüssigkeit arbeitet.
![\includegraphics[height=0.2\textheight]{aggregatszustaende-002}](img2438.gif)
![\includegraphics[height=0.2\textheight]{aggregatszustaende-003}](img2439.gif)
Carnot-Prozess mit verdampfender Flüssigkeit
|
Der Prozess läuft folgendermassen ab
|
|
Die Flüssigkeit | verdampft isobar und isotherm |
|
|
Der Dampf | expandiert adiabatisch |
|
|
Der Dampf | kondensiert isobar und isotherm |
|
|
Die Flüssigkeit | wird erwärmt |
Wenn ![]() genügend klein ist sind die Prozesse
genügend klein ist sind die Prozesse
![]() und
und
![]() isochor.
isochor.
Diese Carnot-Maschine leistet die mechanische Arbeit
| (4.622) |
Der Wirkungsgrad wird damit
Hier ist ![]() die spezifische Verdampfungsenergie (Energie pro Masse). Ebenso sind
die spezifische Verdampfungsenergie (Energie pro Masse). Ebenso sind
![]() und
und
![]() die spezifischen Volumina. Der Wirkungsgrad dieser Carnot-Maschine aus Gleichung (4.351) ist
der gleiche wie für die klassischen Carnot-Prozesse. Durch Umstellen von Gleichung (4.351) erhalten wir die
Clausius-Clapeyron-Gleichung.
die spezifischen Volumina. Der Wirkungsgrad dieser Carnot-Maschine aus Gleichung (4.351) ist
der gleiche wie für die klassischen Carnot-Prozesse. Durch Umstellen von Gleichung (4.351) erhalten wir die
Clausius-Clapeyron-Gleichung.
Die Einheit der spezifischen Verdampfungswärme ist
![$\displaystyle \left[\lambda\right] = \frac{J}{kg}$](img2459.gif) |
Wir möchten den Dampfdruck ![]() als Funktion der Temperatur berechnen. Wir betrachten den Fall, dass das
spezifische Volumen der Flüssigkeitviel kleiner als das spezifische Volumen des Gases ist, also
als Funktion der Temperatur berechnen. Wir betrachten den Fall, dass das
spezifische Volumen der Flüssigkeitviel kleiner als das spezifische Volumen des Gases ist, also
![]() . Diese Ungleichung ist meistens sehr gut erfüllt (bei Wasser ist
. Diese Ungleichung ist meistens sehr gut erfüllt (bei Wasser ist
![]() . Dann
kann in der Clausius-Clapeyron-Gleichung (4.352)
. Dann
kann in der Clausius-Clapeyron-Gleichung (4.352)
![]() gesetzt werden. Wir schreiben für die
ideale Gasgleichung
gesetzt werden. Wir schreiben für die
ideale Gasgleichung
Mit der Molmasse ![]() bekommen wir
bekommen wir
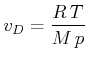 |
Eingesetzt in die Clausius-Clapeyron-Gleichung (4.352) erhalten wir
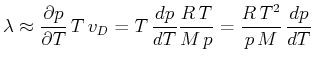 |
(4.625) |
Wir separieren ![]() und
und ![]() und erhalten
und erhalten
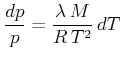 |
(4.626) |
Nach Ausführen der Integration findet man
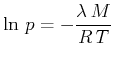 |
(4.627) |
oder
| (4.628) |
Der Druck hängt also exponentiell von der inversen Temperatur ab. Eine Darstellung von ![]() gegen
gegen ![]() ermöglicht die Bestimmung der Steigung
ermöglicht die Bestimmung der Steigung
![]() und damit der spezifischen Verdampfungswärme
und damit der spezifischen Verdampfungswärme ![]() .
Abbildung 4.64 zeigt einige Dampfdruckkurven in der Arrhenius-Darstellung.
.
Abbildung 4.64 zeigt einige Dampfdruckkurven in der Arrhenius-Darstellung.
![\includegraphics[width=0.95\textwidth]{arrhenius}](img2474.gif)
Arrhenius-Darstellung des Dampfdrucks verschiedener
Substanzen (nach [Wea80, D-195]
|
Der Übergang vom Festkörper zur Flüssigkeit heisst Schmelzen. Der umgekehrte Vorgang wird Erstarren oder, bei Wasser, Gefrieren, genannt.
Für die Schmelzwärme gilt eine zur Clausius-Clapeyron-Gleichung analoge Gleichung
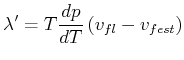 |
(4.629) |
Die Einheit der spezifischen Schmelzwärme ![]() ist
ist
![$\displaystyle \left[\lambda'\right] = \frac{J}{kg}$](img2477.gif) |
Wenn
![]() ist, dann ist
ist, dann ist
![]() . Dies bedeutet, dass unter
Druck die Materie bevorzugt in der festen Phase ist. Bei Wasser ist die
Situation umgekehrt (
. Dies bedeutet, dass unter
Druck die Materie bevorzugt in der festen Phase ist. Bei Wasser ist die
Situation umgekehrt (
![]() ). Damit schmilzt Eis bei hohem Druck.
Durch diesen Effekt werden Gletscher und Schlittschuhe geschmiert.
). Damit schmilzt Eis bei hohem Druck.
Durch diesen Effekt werden Gletscher und Schlittschuhe geschmiert.
Wir betrachten ein System mit einer Teilchensorte (eine Komponente). Für dieses System finden wir die folgende Anzahl von Freiheitsgraden:
| 1 Phase |
|
2 Freiheitsgrade |
|
||
| 2 Phasen |
|
Schmelz-(Dampf-)druckkurve |
|
1 Freiheitsgrad |
|
| 3 Phasen |
|
0 Freiheitsgrade |
Je mehr Phasen wir also haben, desto bestimmter ist das System. Bei einer Komponente und drei Phasen gibt es keine
Freiheitsgrade mehr. Die Gibbsche Phasenregel gibt eine Beziehung für die Anzahl
Freiheitsgrade ![]() , wenn das System aus
, wenn das System aus ![]() Komponenten mit
Komponenten mit ![]() Phasen besteht.
Phasen besteht.
|
Die Gibbsche Phasenregel lautet
|
Aus der Gibbschen Phasenregel folgt, dass der Tripelpunkt von Wasser eindeutig definiert ist.
Othmar Marti