Weiter: Chemische Reaktionen Oben: Wärmelehre Zurück: Aggregatszustände Skript: PDF-Datei Übungen: Blätter
Bei idealen Gasen erfüllen die Teilchensorten das Volumen so, wie wenn sie es alleine ausfüllen würden. Bei
idealen Gasen existieren keine langreichweitigen Kräfte. Die Stösse zwischen den unterschiedlichen Molekülsorten
gleichen die Temperatur aus, so dass alle Molekülsorten die gleiche Temperatur haben. Für die ![]() -te Teilchensorte
können wir also schreiben:
-te Teilchensorte
können wir also schreiben:
| (4.630) |
Mit dem Daltonschen Gesetz (Gleichung (4.359) ) lautet dann die Zustandsgleichung für Mischungen des idealen Gases
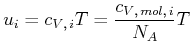 |
Die verschiedenen Molekülsorten des Gasgemisches nehmen den gleichen Raum ein. Die Moleküle wechselwirken, ausser
bei Stössen, nicht miteinander. Deshalb sind die resultierenden Wärmekapazitäten die Summe aus den
Wärmekapazitäten der einzelnen Teilsysteme, unabhängig davon ob ![]() oder
oder ![]() konstant gehalten wird.
konstant gehalten wird.
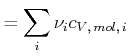 |
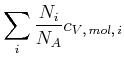 |
(4.634) | ||
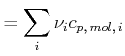 |
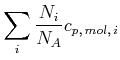 |
(4.635) |
Dabei ist, bei genügend hohen Temperaturen
Bei Gemischen haben wir für die obigen Betrachtungen angenommen, dass jede Molekülsorte das ganze Volumen ![]() einnimmt, dass aber ihr Partialdruck
einnimmt, dass aber ihr Partialdruck ![]() ein Summand des Gesamtdruckes ist. Ebenso gültig ist die Betrachtung,
dass jede Molekülsorte das Teilvolumen
ein Summand des Gesamtdruckes ist. Ebenso gültig ist die Betrachtung,
dass jede Molekülsorte das Teilvolumen ![]() einnimmt, dass nun aber der Druck der Molekülsorte gleich dem
Gesamtdruck
einnimmt, dass nun aber der Druck der Molekülsorte gleich dem
Gesamtdruck ![]() ist.
ist.
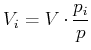 |
(4.638) |
![\includegraphics[width=0.8\textwidth]{thermodynamik-020}](img2507.gif)
|
Wir betrachten als Gedankenexperiment das Teilsystem aus der Abbildung 4.65. Die beiden
Volumina ![]() und
und ![]() sollen gegeneinander verschiebbar sein. Die Membrane (Wand)
sollen gegeneinander verschiebbar sein. Die Membrane (Wand) ![]() , die das
Volumen
, die das
Volumen ![]() nach rechts abschliesst, soll für die Molekülsorte
nach rechts abschliesst, soll für die Molekülsorte ![]() durchlässig, für die Sorte
durchlässig, für die Sorte ![]() aber
undurchlässig sein. Ebenso soll die Membrane
aber
undurchlässig sein. Ebenso soll die Membrane ![]() für die Molekülsorte
für die Molekülsorte ![]() durchlässig und für die Sorte
durchlässig und für die Sorte ![]() undurchlässig sein. Solche halbdurchlässigen Membranen existieren, zum Beispiel in Zellen. Hier wollen wir
annehmen, dass die Membranen für die Molekülsorte, für die sie durchlässig ist, wie nicht-existent sein soll. Die
beiden Membranen
undurchlässig sein. Solche halbdurchlässigen Membranen existieren, zum Beispiel in Zellen. Hier wollen wir
annehmen, dass die Membranen für die Molekülsorte, für die sie durchlässig ist, wie nicht-existent sein soll. Die
beiden Membranen ![]() und
und ![]() bewirken also, dass sich im Überschneidungsgenbiet der beiden Volumina
bewirken also, dass sich im Überschneidungsgenbiet der beiden Volumina ![]() und
und
![]() beide Molekülsorten befinden.
beide Molekülsorten befinden.
Wenn man die beiden Volumina auseinander bewegt, so erzwingen die halbdurchlässigen Membranen, dass die
Molekülsorten ![]() und
und ![]() getrennt werden. Wir wollen nun die beiden Zylinder von aussen um
getrennt werden. Wir wollen nun die beiden Zylinder von aussen um ![]() auseinander
bewegen. Dabei soll der Zylinder
auseinander
bewegen. Dabei soll der Zylinder ![]() ruhend sein.
ruhend sein.
|
Die gesamte mechanische Arbeitsleistung ist dabei
| (4.639) | ||
| (4.640) |
Bei ![]() Komponenten jeweils mit der Molzahl
Komponenten jeweils mit der Molzahl ![]() ist die Gesamtentropie
ist die Gesamtentropie
| Dieser Stoff wurde am 16. 07. 2007 behandelt |
|
|
Materialien
Folien zur Vorlesung am 16. 07. 2007 PDF |
Wir betrachten ![]() Komponenten mit den Molzahlen
Komponenten mit den Molzahlen ![]() und der Temperatur
und der Temperatur ![]() , die getrennt sein sollen. Der
Druck jeder Komponente
, die getrennt sein sollen. Der
Druck jeder Komponente ![]() wird durch isotherme Kompression auf den gewünschten Druck des Gesamtsystems,
wird durch isotherme Kompression auf den gewünschten Druck des Gesamtsystems, ![]() ,
gebracht. Die jeweiligen Teilvolumina sind dann
,
gebracht. Die jeweiligen Teilvolumina sind dann ![]() . Die Gesamtentropie
. Die Gesamtentropie ![]() der
der ![]() getrennten Teilsysteme ist
einfach die Summe der Teilentropien.
getrennten Teilsysteme ist
einfach die Summe der Teilentropien.
| Die Diffusion ist ein irreversibler Prozess! |
Die Verhältnisse des Gesamtdrucks zu den Partialdrucken sind proportional zu den Verhältnissen der Gesamtteilchenzahl zu den Teilchenzahlen der Teilkomponenten
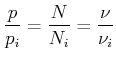 |
Damit ist die Entropiezunahme bei der diffusiven Mischung von ![]() Teilchenzahlen
Teilchenzahlen
|
Die Grösse
ist die Mischungsentropie bei der Mischung von |
Wenn wir nun zwei Volumina voll mit gleichartigen Molekülen mischen, müsste natürlich
Aus der Unmöglichkeit des kontinuierlichen Übergangs muss man schliessen, dass Atome nur in diskreten Zuständen vorkommen können.
Beispiel:
Edelgase als beste Approximationen des idealen Gases zeigen die Mischungsentropie. Sogar Orthowasserstoff und Parawasserstoff (zwei Spinzustände) sind nicht ohne Entropiezunahme mischbar.
Bei Systemen mit mehreren Molekülesorten sind die Anzahlen ![]() thermodynamische Zustandsgrössen. Wir hatten
früher die Entropie als Funktion der inneren Energie und des Volumens betrachtet:
thermodynamische Zustandsgrössen. Wir hatten
früher die Entropie als Funktion der inneren Energie und des Volumens betrachtet:
Wir nehmen zuerst an, dass alle ![]() konstant sind. Dies ist gleichbedeutend, dass keine chemischen und
kernphysikalischen Reaktionen vorkommen. Das Differential der Entropie war durch
konstant sind. Dies ist gleichbedeutend, dass keine chemischen und
kernphysikalischen Reaktionen vorkommen. Das Differential der Entropie war durch
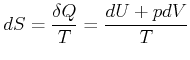 |
(4.649) |
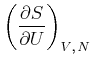 |
||
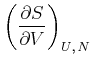 |
(4.650) |
Unsere Diskussion der verallgemeinerten Kräfte legt nahe, dass zur extensiven Grösse ![]() eine intensive Grösse
eine intensive Grösse
![]() gehören muss. Wir definieren
gehören muss. Wir definieren
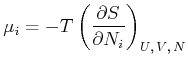 |
(4.651) |
Das vollständige Differential der Entropie ist also
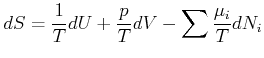 |
(4.652) |
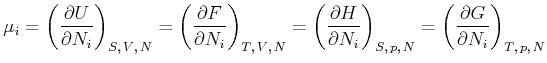 |
(4.653) |
Alle thermodynamischen Potentiale sind extensive Grössen. Zum Beispiel gilt für die freie Enthalpie
![]() bei nur einer Substanz
bei nur einer Substanz
| (4.654) |
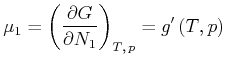 |
(4.655) |
|
Das chemische Potential |
Achtung: Bei mehreren Komponenten ist das chemische Potential nicht die freie Enthalpie pro
Teilchen!
|
Aus der Definition der inneren Energie
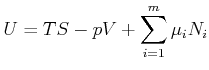 |
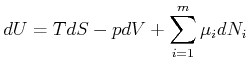 |
Gibbs-Duhem-Gleichung |
(Siehe Sommerfeld, Thermodynamik und Statistik [Som77, pp. 71-77])
Für den Fall, dass neben den intensiven Grössen Druck ![]() und Temperatur
und Temperatur ![]() und den dazu gehörigen extensiven
Grössen innere Energie
und den dazu gehörigen extensiven
Grössen innere Energie ![]() und Volumen
und Volumen ![]() weitere extensive Grössen
weitere extensive Grössen ![]() mit den dazu gehörigen
verallgemeinerten Kräften
mit den dazu gehörigen
verallgemeinerten Kräften ![]() vorhanden sind, kann man den ersten und zweiten Hauptsatz zusammenfassen. Die
Grössen
vorhanden sind, kann man den ersten und zweiten Hauptsatz zusammenfassen. Die
Grössen ![]() sind allgemein. Die Teilchenzahl
sind allgemein. Die Teilchenzahl ![]() ist nur ein Beispiel.
ist nur ein Beispiel.
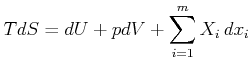 |
(4.659) |
Bei variablen Teilchenzahlen ist ![]() und die dazugehörigen
verallgemeinerten Kräfte
und die dazugehörigen
verallgemeinerten Kräfte
![]() . Wir haben also
. Wir haben also
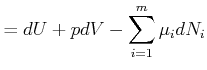 |
||
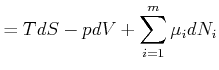 |
(4.660) |
Analog bekommen wir
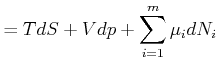 |
(4.661) | |||
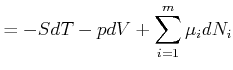 |
(4.662) | |||
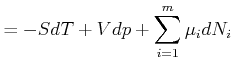 |
(4.663) |
Daraus bekommen wir durch Ableiten
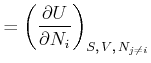 |
(4.664) | |
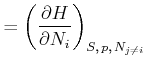 |
(4.665) | |
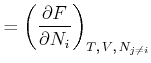 |
(4.666) | |
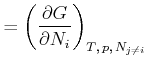 |
(4.667) |
Analog zu früher können wir weiter Maxwellrelationen aus den zweiten
Ableitungen bestimmen. Betrachten wir ![]() .
.
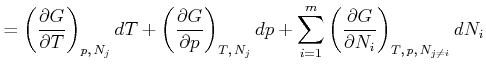 |
||
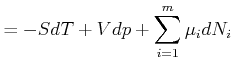 |
(4.668) |
Daraus ergibt sich zum Beispiel
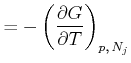 |
(4.669) | |
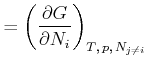 |
(4.670) |
Die zweiten Ableitungen müssen von der Reihenfolge unabhängig sein, also
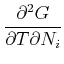 |
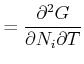 |
|
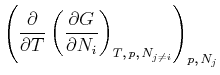 |
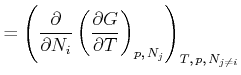 |
|
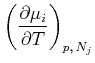 |
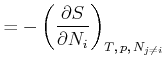 |
(4.671) |
Wir betrachten nun ein Zweiphasensystem als ein System aus zwei Komponenten ![]() und
und ![]() . Zum Beispiel
könnte
. Zum Beispiel
könnte ![]() die Anzahl Teilchen von
die Anzahl Teilchen von ![]() in der Gasphase und
in der Gasphase und ![]() die Anzahl der
die Anzahl der ![]() -Teilchen in der
Flüssigphase sein.
-Teilchen in der
Flüssigphase sein.
![\includegraphics[width=0.2\textwidth]{thermodynamik-177}](img2601.gif)
Zweiphasensystem als System zweier Komponenten
|
Es gilt:
Weiterhin muss die Entropie
| (4.673) |
| (4.674) |
| (4.675) |
Wir führen die Differentiation aus und erhalten
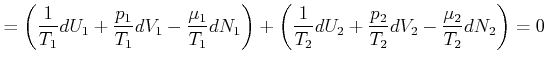 |
||
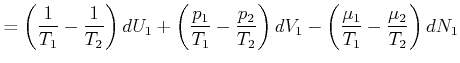 |
(4.676) |
Wie immer müssen die Vorfaktoren der einzelnen Differentiale einzeln verschwinden. Daraus folgt
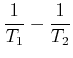 |
||||||
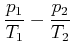 |
||||||
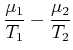 |
(4.677) |
Wir kommen also zur Aussage:
| Im Phasengleichgewicht sind Temperatur, Druck und die chemischen Potentiale gleich. |
Bei reinen Phasen gilt auch:
![]() (Gleichheit der freien Enthalpie pro
Molekül)
(Gleichheit der freien Enthalpie pro
Molekül)
Sind verschiedene Teile eines Gesamtsystems im Gleichgewicht, gilt allgemein
| (4.678) |
Othmar Marti