Weiter: Osmose Oben: Wärmelehre Zurück: Mehrstoffsysteme, Lösungen Skript: PDF-Datei Übungen: Blätter
| Dieser Stoff wurde am 19. 07. 2007 behandelt |
|
|
Materialien
Folien zur Vorlesung am 19. 07. 2007 PDF |
Beispiel:
Die Knallgasreaktion wird so beschrieben
Allgemein werden chemische Reaktionen durch Gleichungen des Typs
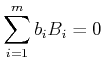 |
(4.679) |
Beispiel:
Für die Knallgasreaktion gilt die Relation:
![]() .
.
Wie immer muss die Entropie
![]() maximal werden. Das heisst:
maximal werden. Das heisst: ![]() .
Wir nehmen adiabatisch isochore Bedingungen an. Dann müssen
.
Wir nehmen adiabatisch isochore Bedingungen an. Dann müssen ![]() und
und ![]() konstant sein. Damit gilt für die
Teilchenzahlen
konstant sein. Damit gilt für die
Teilchenzahlen
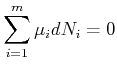 |
(4.681) |
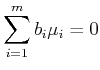 |
(4.682) |
Wir betrachten die chemische Reaktion als Mischung. Die Mischungsentropie ist
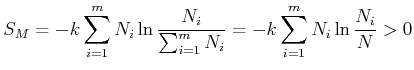 |
(4.683) |
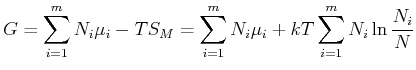 |
(4.684) |
Zur Berechnung des Gleichgewichtes verwenden wir
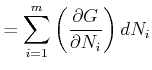 |
(4.685) |
Eine Komponente
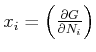 ist dann
(wobei
ist dann
(wobei
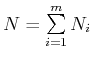 ist)
ist)
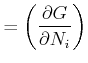 |
||
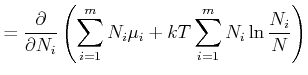 |
||
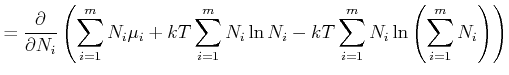 |
||
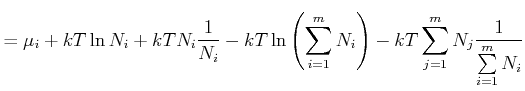 |
||
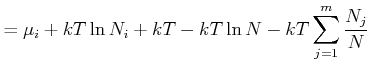 |
In jedem Summanden, ausser dem letzten, bleibt nur der Term mit ![]() nach dem Ableiten übrig. Im letzten
Summanden kann man für beliebige
nach dem Ableiten übrig. Im letzten
Summanden kann man für beliebige ![]() nach
nach ![]() ableiten, da
ableiten, da ![]() im Logarithmus vorkommt. Damit wird
im Logarithmus vorkommt. Damit wird
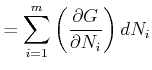 |
||
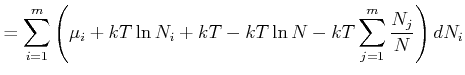 |
||
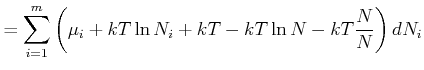 |
||
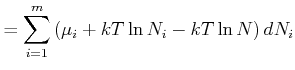 |
(4.686) |
mit
| (4.687) |
erhalten wir
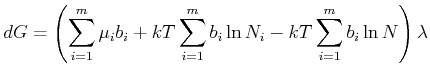 |
(4.688) |
Da ![]() im Gleichgewicht ist, erhalten wir für
im Gleichgewicht ist, erhalten wir für
![]()
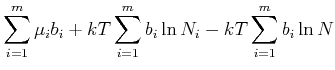 |
||
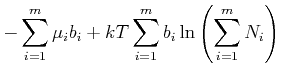 |
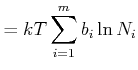 |
|
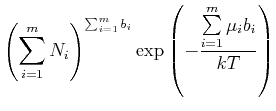 |
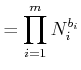 |
(4.689) |
Bei abgeschlossenen Systemen ist die Grösse
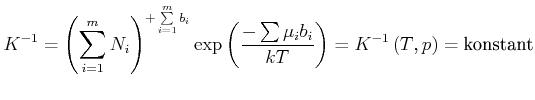 |
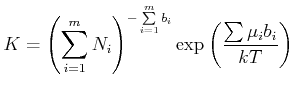 |
(4.691) |
Beispiel:
Für die Knallgsreaktion gilt
![]() wobei
wobei
![]() . Daraus folgt
. Daraus folgt
Nur wenn
![]() ist, ist das Reaktionsgleichgewicht unabhängig vom Druck. In allen anderen Fällen kann
über den Druck
ist, ist das Reaktionsgleichgewicht unabhängig vom Druck. In allen anderen Fällen kann
über den Druck ![]() die Gleichgewichtslage der chemischen Reaktion eingestellt werden.
die Gleichgewichtslage der chemischen Reaktion eingestellt werden.
Wir können Gleichung (4.420) auch mit molaren Grössen schreiben
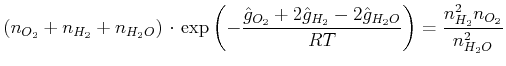 |
(4.693) |
Wenn die molaren Enthalpien der Edukte (Ausgangsstoffe) gross gegen die molaren Enthalpien der Produkte sind, liegt das Gleichgewicht bei den Produkten.
Formulierung mit der Gleichgewichtskonstante ![]()
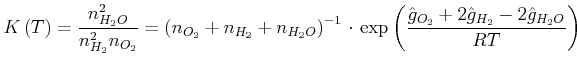 |
(4.694) |
Wenn ![]() gross ist,liegt das Gleichgewicht bei
gross ist,liegt das Gleichgewicht bei ![]() .
.
Wenn ![]() klein ist verschiebt sich das Gleichgewicht zu
klein ist verschiebt sich das Gleichgewicht zu ![]() ,
, ![]()
Aus den thermodynamischen Potentialen erhalten wir den Zusammenhang
![]() ist die freiwerdende Reaktionsenthalpie, da die Entropieänderung nicht als Wärme messbar ist.
Wir haben also
ist die freiwerdende Reaktionsenthalpie, da die Entropieänderung nicht als Wärme messbar ist.
Wir haben also
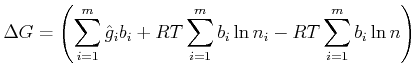 |
(4.696) |
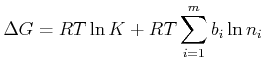 |
(4.697) |
Abhängig von den ![]() 's kann
's kann ![]() positiv oder negativ sein. Der Standard-Wert für die freie Enthalpie pro
mol wird üblicherweise mit
positiv oder negativ sein. Der Standard-Wert für die freie Enthalpie pro
mol wird üblicherweise mit
| (4.698) |
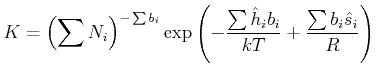 |
(4.699) |
Man bekommt
![]() , wenn man
, wenn man ![]() gegen
gegen
![]() aufträgt
(Arrhenius-Darstellung)
aufträgt
(Arrhenius-Darstellung)
![\includegraphics[width=0.6\textwidth]{thermodynamik-178}](img2683.gif)
|
Zusammengefasst bedeutet dies
![\includegraphics[width=0.6\textwidth]{thermodynamik-179}](img2685.gif)
|
Chemische Reaktionen können mit Reaktionskoordinaten wie in der Abbildung 4.68
beschrieben werden. Die Ausgangssstoffe auf der linken Seite müssen dabei die Barriere ![]() überwinden, um
nach rechts reagieren zu können. Umgekehrt ist die Barriere
überwinden, um
nach rechts reagieren zu können. Umgekehrt ist die Barriere
![]() . Die Anzahl Teilchen, die die
Barriere überwinden können ist proportional zu
. Die Anzahl Teilchen, die die
Barriere überwinden können ist proportional zu
Othmar Marti