
Weiter: Physikalische Begründung der geometrischen Oben: Optische Instrumente Zurück: Das Teleskop oder Fernrohr Skript: PDF-Datei Übungen: Blätter
(Siehe Hecht, Optik [Hec, pp. 106, 284]) (Siehe Pérez, Optik [Pér96, pp. 415]) (Siehe Tipler, Physik [TM04, pp. 1038])
|
|
Im allgemeinen Falle hängt die Phasengeschwindigkeit einer Welle von der Frequenz und vom Medium ab. Das heisst für Licht, dass jede Farbe eine eigene Ausbreitungsgeschwindigkeit hat.
![\includegraphics[width=0.53\textwidth]{prisma}](img225.gif)
![\includegraphics[width=0.4\textwidth]{dispersion-kurve}](img226.gif)
Links: Strahlengang durch ein Prisma. Rechts: Dispersion einiger
Materialien
|
|
|
Durch die Dispersion des Lichtes, das heisst, dass die Brechzahl von der Wellenlänge abhängt, werden die verschiedenen Farben unterschiedlich gebrochen. Jedes Mal, wenn Licht durch die Grenzfläche Luft-Materie geht, werden unterschiedliche Farben unterschiedlich gebrochen. Dies bewirkt die folgenden Effekte:
Um die Physik der Dispersion zu klären, müssen wir ein physikalisches Modell finden, bei dem eine Frequenzabhängigkeit auftritt. Wir erinnern uns aus der Mechanik, dass bei Oszillatoren eine Resonanz auftritt. Als Beispiel kann man ein Feder-Masse-System betrachten.
![\includegraphics[width=0.8\textwidth]{feder-masse-modell}](img228.gif)
Modell eines Oszillators
|
In diesem Feder-Masse-Modell wird die Schwingung durch
![]() angeregt. Die Amplitude verhält sich als Funktion der Frequenz
wie
angeregt. Die Amplitude verhält sich als Funktion der Frequenz
wie
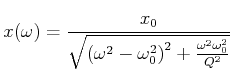 |
(3..8) |
![\includegraphics[width=0.45\textwidth]{dispersion-oszi-modell-1}](img231.gif)
![\includegraphics[width=0.45\textwidth]{dispersion-oszi-modell-2}](img232.gif)
Resonanzkurve links als Funktion der Frequenz
|
Aus diesen Kurven gewinnt man die Anregung, dass ein Feder-Masse-System als Modell für die Dispersion geeignet sein könnte.
![\includegraphics[width=0.8\textwidth]{dispersion-elektronenhuelle}](img235.gif)
Links liegt die Elektronenwolke zentriert über dem positiv geladenen
Kern. Wenn ein elektrisches Feld
|
Ein fester Körper besteht aus Atomen. Diese bestehen aus Elektronen, deren
Aufenthaltswahrscheinlichkeit über einen Durchmesser von ![]() ausgeschmiert
ist, sowie aus einem Atomkern, der im Zentrum der Elektronenwolke
liegt und einen Durchmesser von ungefähr
ausgeschmiert
ist, sowie aus einem Atomkern, der im Zentrum der Elektronenwolke
liegt und einen Durchmesser von ungefähr ![]() hat. Wenn ein elektrisches Feld
hat. Wenn ein elektrisches Feld
![]() angelegt wird, dann verschiebt sich die Elektronenwolke gegen den
Kern um eine Distanz
angelegt wird, dann verschiebt sich die Elektronenwolke gegen den
Kern um eine Distanz ![]() . Diese Verschiebung soll klein gegen den
Durchmesser der Elektronenwolke sein. Dann können wir annehmen, dass die Ladung
der Elektronenwolke homogen verteilt ist. Da das Coulombgesetz für die
elektrostatischen Kräfte die gleiche Form wie das Gravitationsgesetz hat, hängt
die Kraft für die Testladung des Kerns linear von der Auslenkung ab, und zwar
so, dass der Schwerpunkt des Kerns und der der Elektronenwolke wieder
übereinander gelegt werden sollen. Wir haben also eine zur Auslenkung
proportionale rücktreibende Kraft, wie bei einer Feder.
. Diese Verschiebung soll klein gegen den
Durchmesser der Elektronenwolke sein. Dann können wir annehmen, dass die Ladung
der Elektronenwolke homogen verteilt ist. Da das Coulombgesetz für die
elektrostatischen Kräfte die gleiche Form wie das Gravitationsgesetz hat, hängt
die Kraft für die Testladung des Kerns linear von der Auslenkung ab, und zwar
so, dass der Schwerpunkt des Kerns und der der Elektronenwolke wieder
übereinander gelegt werden sollen. Wir haben also eine zur Auslenkung
proportionale rücktreibende Kraft, wie bei einer Feder.
Deshalb nehmen wir an, dass das Elektron-Kern-System als Feder-Masse-System beschrieben werden kann. Da ein Elektron nicht nur Kräfte auf seinen Kern, sondern auch auf die benachbarten ausübt, müssen wir ein dreidimensionales Netz von Federn und Massen betrachten. Wir vereinfachen das System hier auf eine lineare Federkette.
![\includegraphics[width=0.8\textwidth]{dispersion-federmodell}](img240.gif)
Federmodell für die Dispersion nach (Siehe Känzig, Mechanik und Wellenlehre [Kän78, pp. 292]) .
|
Wir betrachten eine longitudinale Welle auf einem Feder-Masse-System. Die Bewegungsgleichung für die n-te Masse ist
| (3..9) |
Wir setzen
![]() und erhalten
und erhalten
![$\displaystyle \ddot\xi_n = \Omega_0^2\left[\frac{1}{4}\left(\xi_{n+1}+\xi_{n-1}\right)-\frac{1}{2}\xi_n\right]$](img247.gif) |
(3..10) |
| (3..11) |
![$\displaystyle = \Omega_0^2\left[\frac{1}{4}\left(e^{ik(n-1)a} + e^{ik(n+1)a}\right) -\frac{1}{2}e^{ikna}\right]$](img253.gif) |
||
![$\displaystyle = \frac{1}{2}\Omega_0^2\left[1-\frac{1}{2}\left(e^{ika}+e^{-ika}\right)\right]$](img255.gif) |
||
![$\displaystyle = \frac{1}{2}\Omega_0^2\left[1-\cos(ka)\right]$](img256.gif) |
||
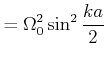 |
(3..12) |
Die Dispersionsbeziehung für die Feder-Masse-Kette ist
|
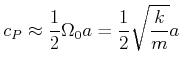 |
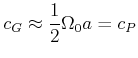 |
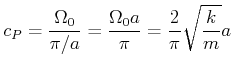 |
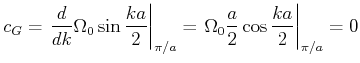 |
Wir können das Gefundene auf das Problem des Brechungsindexes wie folgt zurückrechnen:
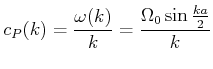 |
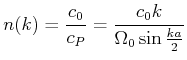 |
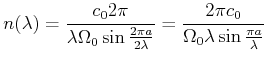 |
|
|
![\includegraphics[width=0.8\textwidth]{dispersion-federmodell-diatomic}](img312.gif)
![\includegraphics[width=0.7\textwidth]{dispersion-diatomic}](img313.gif)
Dispersionsrelation für Federketten mit zwei unterschiedlichen Atomen.
|
Wenn eine Federkette mit einer regelmässigen Anordnung zweier ungleicher Massen
gebildet wird, tritt zum von den vorherigen Ausführungen bekannten
akustischen Zweig ein optischer Zweig. Zusätzlich gibt es Frequenzen, für
die es keinen reellen ![]() -Vektor gibt. Diese Frequenzen (oder über
-Vektor gibt. Diese Frequenzen (oder über
![]() auch diese Energien) sind keine propagierenden Wellen möglich.
Gibt es neben longitudinalen auch transversale Wellen, zeigt die
Dispersionsrelation nicht einen sondern drei Zweige akustischer Phononen.
auch diese Energien) sind keine propagierenden Wellen möglich.
Gibt es neben longitudinalen auch transversale Wellen, zeigt die
Dispersionsrelation nicht einen sondern drei Zweige akustischer Phononen.
Schwerewellen im tiefen Wasser haben die Dispersionsbeziehung
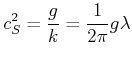 |
(3..14) |
Eine Konsequenz ist, dass sehr lange Wellen sehr schnell sind (Bsp. Tsunamis)
Ein Puls oder eine Wellengruppe besteht aus Wellen benachbarter Frequenz.
Analog zur Modulation3.1 besteht ein Puls aus einer Einhüllenden sowie einer Phase, die
für sich aber keine Information trägt. Eine längere Rechnung[Kän78]
ergibt, dass die resultierende Wellenfunktion aus harmonischen Welle
![]() sowie der Modulation
sowie der Modulation
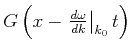 . Die resultierende
Welle ist
. Die resultierende
Welle ist
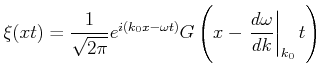 |
(3..15) |
Die Gruppengeschwindigkeit
|
Bei unserem Feder-Masse-System ist ![]() wenn
wenn
![]() ist. Das heisst,
der Puls, der die Information trägt, ist ortsfest. Wenn
ist. Das heisst,
der Puls, der die Information trägt, ist ortsfest. Wenn ![]() nicht
konstant ist, bewegen verändert sich die Form des Pulses, da die verschiedenen
Frequenzanteile sich unterschiedlich schnell ausbreiten.
nicht
konstant ist, bewegen verändert sich die Form des Pulses, da die verschiedenen
Frequenzanteile sich unterschiedlich schnell ausbreiten.
|
|
Lösungsmöglichkeiten
Othmar Marti